CodeForces-Split Plus K

题目

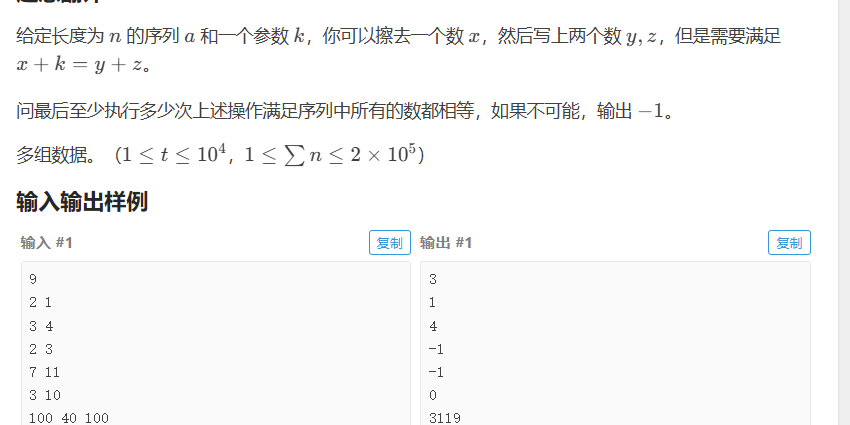
题目不可能情况思考

对x+k=y+z这个式字分析，你会分析如果x<k，那么所得总和必然小于2*k，大于则相反，有了这个知识，就可以知道输出-1的情况是哪些了

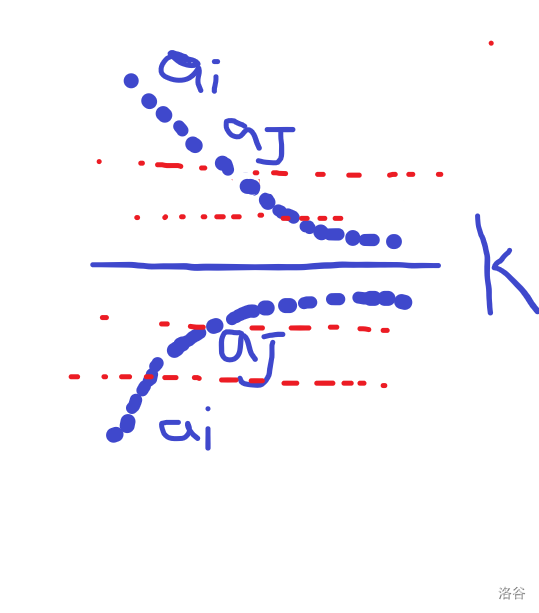
其实再加k然后分摊出去，就是一个稀释的过程。

---

最终必然会导致x趋向于一个中间值，即k与aMAX的中间某条红线那。

---

如果说存在一头一尾在k两端的，那肯定是不可能的，因为+k对于上面的平摊出来肯定是总和大于2*k的，可能分出一个小于k的一个大于k的，但是对于那个大于k的，再分下去还是永远会存在下一个大于k的值，

---

然后那个小于k的同理，永远存在一个小于k的存在，所以这个x不可能存在的，这就是-1的情况

做题思路

cf的题，正面思考很难，那就从反面着手

我们假设找到了那个x
对于任何一个时刻分裂出x的等式都存在
Ai+k=x+Aii
物理公式经常有Δ这玩意出来
比如Δt，Δv什么的
这里面我们可以发现Ai-Aii=Δ，这是这个式子求出x时的变化值。而且你会发现对于ai，aj来说这个Δ都是相同的，
Δ=x-k，就是x-k，那么我们可以列出一个式子：
ai+（t-1）*k=tx，其中t-1次操作，
然后拆开一看
（ai-k）/t=x-k=Δ
然后求次数最小 不就是（ai-k）/Δ=t吗 其中Δ越大越好，
t就越小，t-1也就越小
所以问题来到求Δ最大

那么如何求呢

你会发现这个Δ对于每个人都要相同，并且还要保证（ai-k）/Δ是整数，

---

那自然就可以想到Δ是每个ai-k的除数，都是可以%=0的，那对于所有人来说这个Δ都尽量大，那不就是最大公约数吗？

---

如此，这道题就迎刃而解了，然后注意下细节就是

---

所有数都等于k时 你会发现最大公约数ai-k这样算是0
然后对于c++来说，虽然你调用了gcd函数，但是某个数%0是肯定错误的，会re，所以要特判

---

最后答案要-1，因为t-1次操作

除数为零或模数为零。这一点是比赛里出题人喜欢搞的，让你特判。所以思考问题要全面。
 cout<<a/0;这种就是错的
约定LCM[0,a]=0，GCD[0,a]=|a|，LCM[a,a]=|a|，GCD[a,a]=|a|

---

---

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
ll  a[200005];
void solve()
{
	int n=0;
	cin>>n;
	ll k=0;
	cin>>k;
	for(int i=1;i<=n;i++)cin>>a[i];
	//正难则反 切记切记切记切记
    sort(a+1,a+1+n);
	if(a[1]<k&&a[n]>=k){cout<<"-1"<<endl;return ;}
	else 	if(a[1]<=k&&a[n]>k){cout<<"-1"<<endl;return ;}
	else  if(a[1]==k&&a[n]==k){cout<<"0"<<endl;return ;}
	ll delta=0;
	// gcd(0,a)==a
	for(int i=1;i<=n;i++)delta=__gcd(delta,abs(a[i]-k));
    //delta=x-k
    ll ans=0;
	for(int i=1;i<=n;i++)
	{
		ans+=(abs(a[i]-k))/delta-1;
	}//忘了abs了
    cout<<ans<<endl;
	return ;
}
int main()
{
	
	int t;
	cin>>t;
	while(t--)solve();
	
	return 0;
	
}