树状数组-算法

题目

题目

对于
&这个操作符不是相同就是1 而是只有两个都是1 才算1 两个0是0

---

要表示-3的二进制，通常使用补码表示法。首先，我们需要找到3的二进制表示，然后取其补码。

1+1=0 0+1=1

---

3的二进制表示为: 0000 0011

接下来，我们需要取其补码，即反码加1：

反码：1111 1100

加1： ---------

1111 1101

因此，-3的二进制表示为1111 1101。

特别的 对于 类似于

4

100

反码 011 加一 100

---

对于点查 可以自己手动模拟下，就能懂了用了差分原理，那个s就是 f一样

d[j]=fi+fi+1+f....fj
 
di = f1+f2+...+fi  ，di = d(i-1) + f
    
 反正很神奇这个东西
 
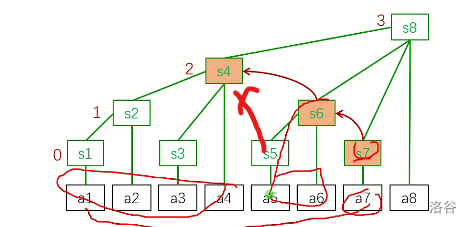
假设n=6 7，8不看

比如说 先给1-4加2 然后要访问 6怎么办呢

按照代码写法操作后 此时

s2=s4=2，s5=s6=-2

然后第六个数是这样算的
a6+query6
其中query6=s6+s4 =0
所以就是a6
对于5的计算 是s5+s4
因为5&-5=1 所以返回s4

对于点修
query(y)-query(x-1)
query(y) 包含了区间 【1, y】 的和，
而 query(x-1) 包含了区间
【1, x-1】 的和。通过相减，可以得到区间 【x, y】 的和。

#include<iostream>
using namespace std;
int n,m;
int s[500005];
int a[500005];
int lowbit(int x)
{
   return x&-x;
}
void change(int x,int k)
{
   while(x<=n)s[x]+=k,x+=lowbit(x);
}
int query(int x)
{
   int t =0;
   while(x)t+=s[x],x=x-lowbit(x);
   return t;
}
int main()
{  
   cin>>n>>m;
   int op,x,y;
   for(int i=1;i<=n;i++)
   {
   	cin>>a[i];
   }
   int k;
   for(int i=1;i<=m;i++)
   {
   	cin>>op>>x;
   	if(op==1){
   		cin>>y>>k;
        change(x,k);
   		change(y+1,-k);

   	}else cout<<a[x]+query(x)<<endl;
   }
   
   
   return 0;
}

---

点查

#include<iostream>
using namespace std;
int n,m;
int s[500005];
int lowbit(int x)
{
   return x&-x;
}
void change(int x,int k)
{
   while(x<=n)s[x]+=k,x+=lowbit(x);
}
int query(int x)
{
   int t =0;
   while(x)t+=s[x],x=x-lowbit(x);
   return t;
}
int main()
{  
  cin>>n>>m;
   int op,x,y;
   for(int i=1;i<=n;i++)
   {
   	cin>>y;
   	change(i,y);
   }
   for(int i=1;i<=m;i++)
   {
   	cin>>op>>x>>y;
   	if(op==1)change(x,y);
   	else cout<<query(y)-query(x-1)<<endl;
   }
   
   
   return 0;
}