生成函数的应用---总结

前言

董老师 一上来就弄了很多的泰勒展开式，高数逃课又没学，我只好开始背了。

对于第一个与第四个

第四个就是第一个的导数

别的都是正常带入变量而已

其实就是普通生成函数和指数生成函数，只不过没有ai，bi了 没别多的项了

对于

1-x^{3=(1-x)*(1+x+x}2)

1-x^4=(1-x2)*(1+x^{2)=(1-x)*(1+x)*(1+x}2)=1+x+x^2+x3

再是广义二项式定理

首先是二项式定理
(a+b)^n=C(i,n) * a^(n-i) * b^i

（1+x）^{n=∑(n,i=0)C(i,n)x}i

如果C(i,-n)就会变成

( -n ) * ( -n+1 ) .... ( -n-i+1 )  /i!

= ( -1 )^ i * ( n* ( n + 1 ) ....n+i-1)/ i !

=(-1)^i * C ( i , n+i-1) 

所以
(1+x)^-n = ∑(∞,i=0)C(i,-n)x^i

=∑(∞,i=0)(-1)^i*C(i,n+i-1)*x^i 

下面来一道例题 暗网的uoj进不去

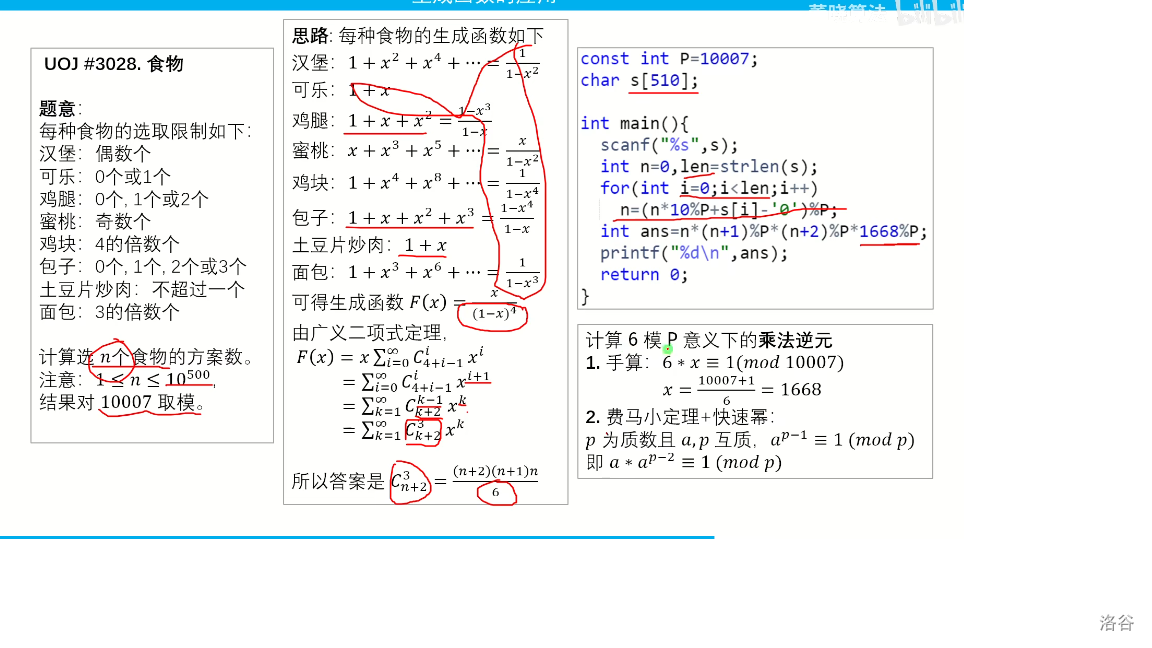
可以发现 其实这可以就是数学化简，然后对于6的逆元

手算这个很有学习的意义！
6*x=1(mod10007)
所以
x=100007+1/6=1668

最后一道例题

POJ 3734 Blocks

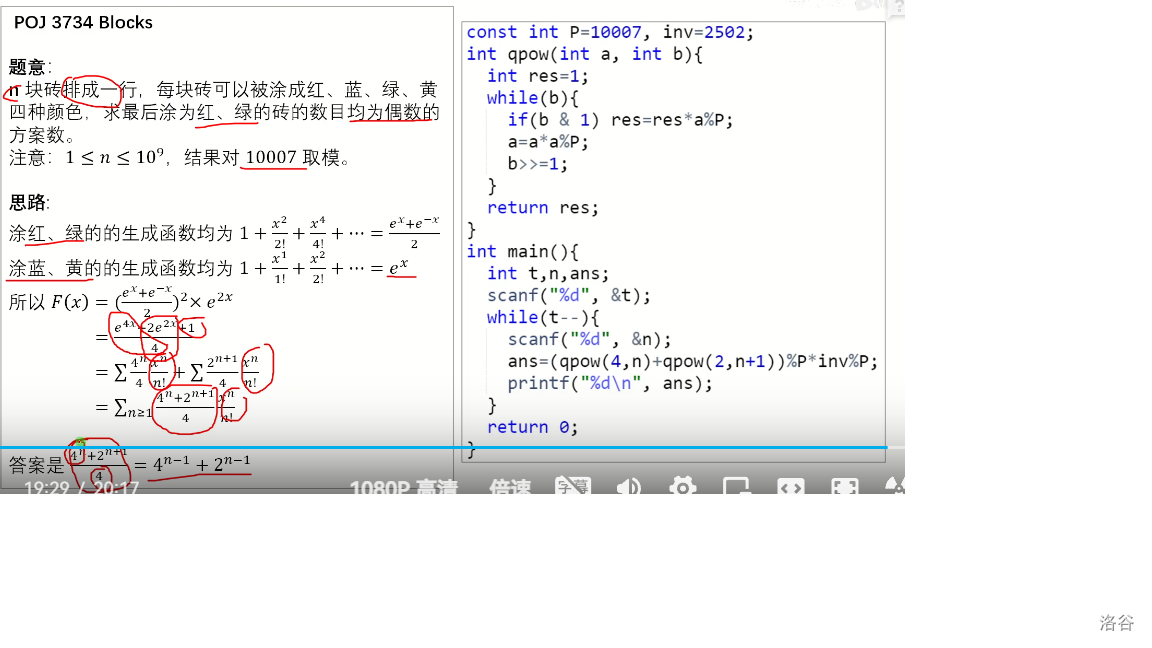
发现x^n/n!的系数就是答案
其实这是一道指数题
代码明天补
最后
要睡觉了 明天要继续加油！！！在新的机房好好学习

#include<iostream>
#define int long long 
#define endl '\n'
const int mod=1e4+7;
using namespace std;
const int range=2e5+10;
int n;
int a[range];
int qpow(int a,int n)
{
	int ans=1;
	while(n)
	{
		
		if(n&1)ans=ans*a%mod;
		a=a*a%mod;
		n>>=1;
	}
	return ans%mod;
}
void solve()
{
	
	cin>>n;
	int ans=0;
	ans=(qpow(4,n-1)+qpow(2,n-1))%mod;
	cout<<ans<<endl;
}
signed main()
{
	ios::sync_with_stdio();
	cin.tie(0);
	cout.tie(0);
	int t;
	cin>>t;
	while(t--)
		solve();
	return 0;
	
	
} 

今天写了下发现里面的常数1要省略。。。。
我当时还琢磨怎么弄掉 。。。。