整除分块-个人总结

题目

前言

今晚上看和式的变换，顺便学习了整除分块 其实就是个分类 很简单的 也不知道为什么定为蓝题

对于∑(i,n)[n/i]向下取整

很明显 这个答案会有很多重复，但我们很容易想到归类他们，把他们分为一类，这就是分块的思想

对于整除分块

第一个性质

块数最多有 2*[sqrt(n)]个

当i<=[sqrt(n)]时

这很明显 这时候都不会重复

i>sqrt(n) [n/i]<=sqrt(n)

最多有[n/i]种取值 不过一般

都达到不了

性质二

i所在的块的右端点位为

[n/([n/i])]

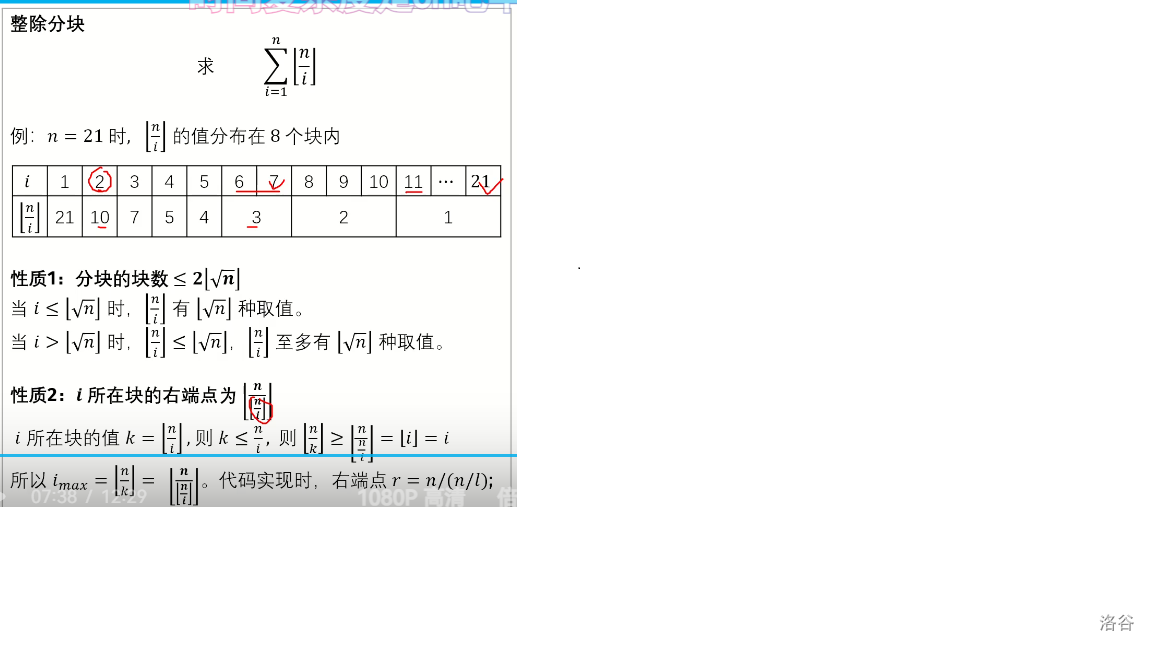
[n/i]此时是块值, 然后用n再除以它最终得到的一定是最右边的那个数 这个不太好解释 反正意会意会
对于块内的元素总和其实就是
里面的元素r-元素l*某个式子即可

题目思路

刚开始我还把这个余数列下来 尝试从这里面进行分块，然后没有卵用，后面看了下 这个k%i竟然可以写成

k-i*[k/i]

于是进行化简 然后就可以做了

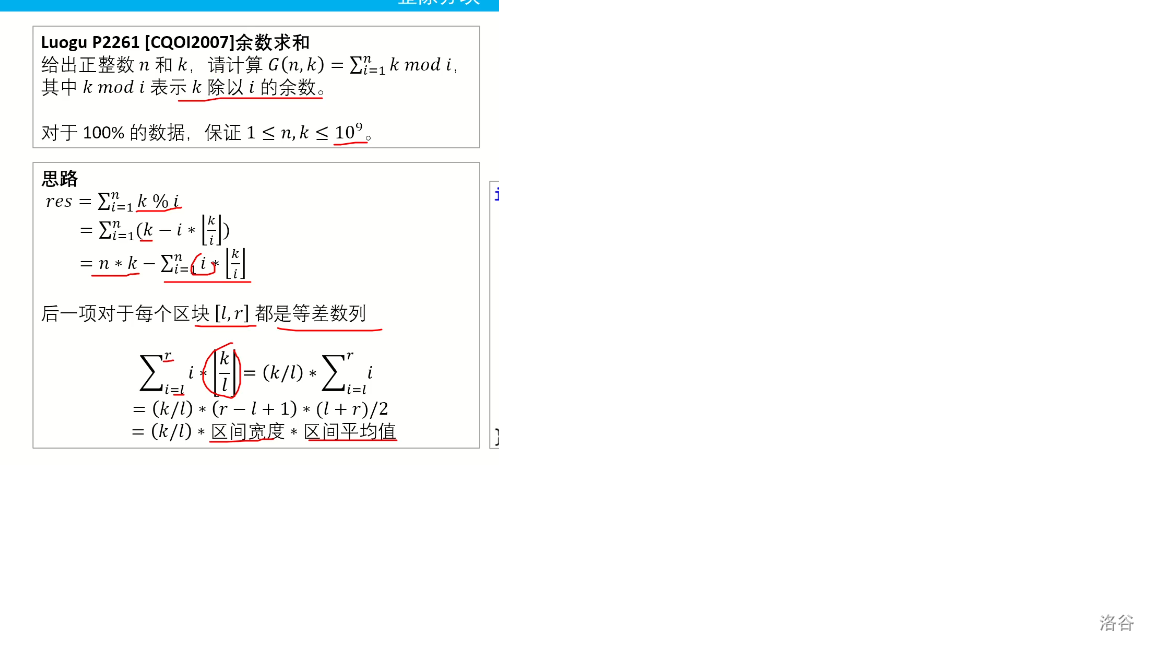
好题一道

最后

明天去南昌了 然后明晚叫施硕统计大名单即可