做题小结4
第一个
非常非常好的一道双指针二分神题 也是我自己想出来的
for (int i = 1; i <= n; i++) {
// cnt=a[i].num;
// while(tot+a[i].num>=0&&r<=n)
while (sum[i] - sum[l - 1] + k < 0) {
l++;
// a[i].l=l;
}
a[i].l = l;
}
这个是延申 采用往后的方式
之前money trees的延申是往前的 就是从后往前遍历
这个while 前缀和用的太好了
nodee check(int mid) {
int len = n - mid + 1;
nodee ans = {0, 0, 0};
for (int i = 1; i <= len; i++) {
if (sum[i + mid - 1] - sum[i - 1] + k >= 0) {
if (a[i + mid - 1].l <= i) {
ans.zhenjia = 1;
ans.l = i;
ans.r = i + mid - 1;
return ans;
}
}
}
return ans;
}
二分的代码 也是很好的
下面是money trees的
int l=1;
int r;
for(int i=1;i<=n;i++)
{
if(h[i-1]%h[i]){
l=i;
}
while(sum[i]-sum[l-1]>k)
{
l++;
}
ans=max(ans,i-l+1);
}
cout<<a
for(int i=n-1;i>=1;i--)
{
if(h[i]%h[i+1]==0)
{
c[i]=c[i+1];
}
else {
c[i]=i;
}
}
这个题 很好
这道题把我做惨了 我用的差分 但是写不出来 这个题 很明显的就是差分完了
数组求和后 你会发现 在遍历满足排列会发现根本不符合逻辑
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int range = 2e5 + 10;
int n;
int a[range];
string s;
int chafen[range];
void solve() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
cin >> s;
s = ' ' + s;
// map<int, int>ma;
for (int i = 1; i <= n; i++) {
if (s[i] == 'B') {
// if (ma[a[i]] >= 1) {
chafen[1]++;
chafen[a[i]+1]--;
// } else ma[a[i]]++;
} else {
if(a[i]>n)continue;
// if (ma[a[i]] >= 1) {
chafen[a[i]]++;
// }
// else ma[a[i]]++;
}
}
for (int i = 1; i <= n; i++) {
chafen[i] += chafen[i - 1];
}
for (int i = 1; i <= n; i++) {
cout << chafen[i] << " ";
}
/*
B:1 5
R:2 2 (3 ,4,5)
*/
cout << endl;
int cnt=0;
for (int i = 1 ; i <= n; i++) {
// if(ma[i])continue;
if (i<=chafen[i]) {
cout<<"ss"<<i<<endl;
cnt++;
continue;
}
else
{
cout<<i<<" "<<cnt<<endl;
cout<<"NO"<<endl;return ;
}
}
cout << "YES" << endl;
return ;
return ;
}
signed main() {
int t ;
cin >> t;
while (t--)
solve();
}
这个判断的过程我试了好久也用了很多办法 上面那个是错的
但是我举个例子 如果4这chafen是有值的 但是你不好把握这个chafen前面有用了吗 如果有用你用个cnt记录下 那么问题来了chafen4是指能来到4的可能次数 前面的使用次数你怎么用一个代数式子表达和chafen4的关系 实在找不到关系 因为这个chafen数组不是前缀和 如果再求他的前缀和更是大错特错 那我来到1的可能方式一万种 求了前缀默认后面一起加起来一万次了
所以看了题解 知道是贪心和排列
每一个块都是有作用的 无论红蓝 所以是红你得保证你不能大的离谱 是蓝你不能小的离谱
我用的二分去写 我以为这个步数是单调的 于是我开始二分 不过二分中检查上限出了逻辑错误 做不出来了 同时我的起点也搞不出来
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int range = 2e5 + 10;
int n;
int m;
string s;
struct node {
int one;
int x, y;
};
node check(int mid) {
int y = n - 1;
int x = m - 1;
int xx = 0;
int yy = 0;
node ans = {0, 0, 0};
for (int i = 1; i <= mid; i++) {
if (s[i] == 'L') xx--;
else if (s[i] == 'R')xx++;
else if (s[i] == 'U')yy++;
else yy--;
if (abs(xx) > x || abs(yy) > y)return ans;
}
vector<char>zy;
vector<char>sx;
map<char, int>ma;
ma['R'] = 1;
ma['L'] = 1;
ma['U'] = 2;
ma['D'] = 2;
for(int i=1;i<=mid;i++)
{
if(ma[s[i]]==1)zy.push_back(s[i]);
else sx.push_back(s[i]);
}
ans.one=1;
if(sx.size()!=0)
{
char ch=sx[0];
int num1=0;
for(auto i:sx)
{
if(i!=ch)break;else num1++;
}if(ch=='U'){
ans.x=1+num1;
}
else ans.x=n-num1;
}
else ans.x=1;
if(zy.size()!=0)
{
char ch=zy[0];
int num2=0;
for(auto i:zy)
{
if(i!=ch)break;else num2++;
}
// cout<<ch<<" "<<num2<<endl;
if(ch=='R'){
ans.y=m-num2;
}
else ans.y=1+num2;
}
else ans.y=1;
return ans;
}
void solve() {
cin >> n >> m;
cin >> s;
if (n == 1 && m == 1) {
cout << 1 << " " << 1 << endl;
return;
}
int l = 1;
int len = s.size();
s = ' ' + s;
int r = len;
node lte = {0, 0, 0};
while (l <= r) {
int mid = l + r >> 1;
node hs = check(mid);
if (hs.one) {
if (mid >= lte.one) {
lte.one = mid;
lte.x = hs.x;
lte.y = hs.y;
}
l = mid + 1;
} else r = mid - 1;
}
cout << lte.x << " " << lte.y << endl;
return ;
}
signed main() {
ios::sync_with_stdio();
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--)
solve();
return 0;
}
// if (zy.size() && sx.size() && ma[s[i - 1]] != ma[s[i]] && i >= 2)
// break;
// else {
// if (ma[s[i]] == 1)zy.push_back(s[i]);
// else sx.push_back(s[i]);
// }
// ans.one = 1;
//// for(auto i:zy)cout<<i<<" ";
//// cout<<endl;
//// for(auto i:sx)cout<<i<<" ";
//// cout<<endl;
// int w = 0;
// for (auto i : sx) {
// if (i == 'U')w++;
// else w--;
// }
// if (w < 0)ans.x = n+w;
// else ans.x = 1+w;
// w = 0;
// for (auto i : zy) {
// if (i == 'R')w++;
// else w--;
// }
// if (w < 0)ans.y = 1-w ;
// else ans.y = m-w ;
// return ans;
很愚蠢的代码 我以为上限就是n-1个 然后左右互相抵消 殊不知互相抵消是对的 我举个例子
LRRLLL 我假设我是3 你觉得这个可能吗
LRR可以存在 接着LLL肯定不行 但是我代码认为可以 因为最终只有2个L
第四个
拓扑排序 不多说了
第五个例题
这题其实我已经做的差不多了 就是不知道拓扑排序 导致没做出来 要是知道了 就可以写出来了 我当时知道深度 然后把他的父亲弄进去但是在这个图片
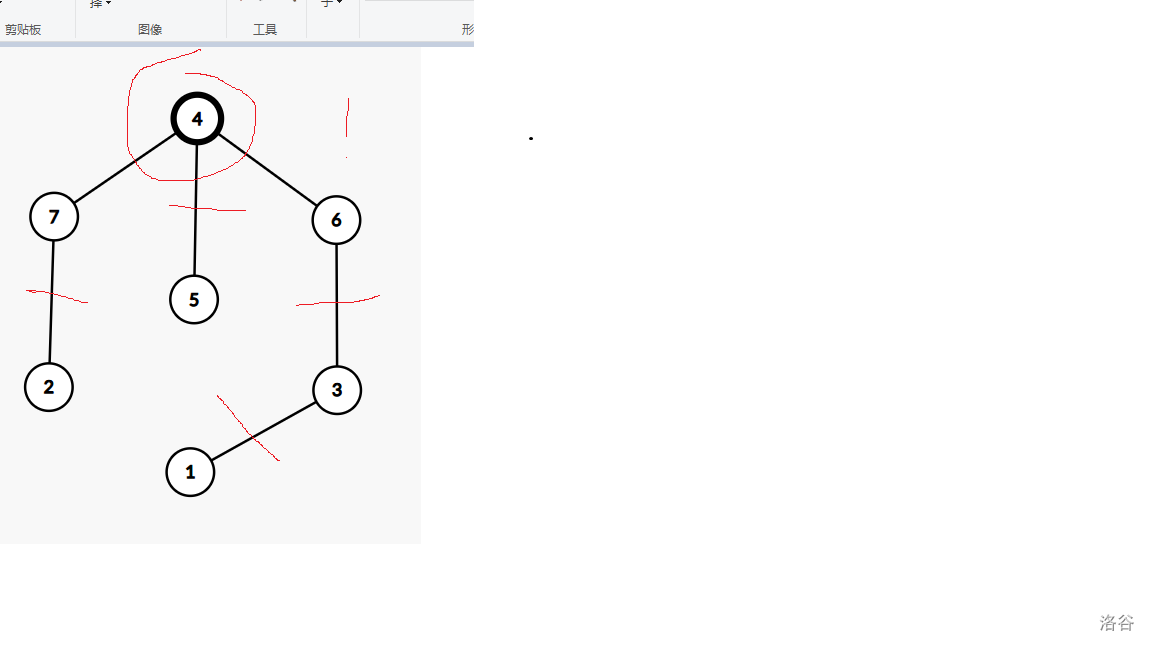
把dep=1减去 然后由于5--->4 我把4弄进新的vector了表示下一步的删除 这是不对的 4还有儿子呢 3-6 把6弄进去是对的
这是错点
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int range=5e5+10;
int n;
int k;int x,y;
int cnt[range];
vector<int>v[range];
int shenxia;
bool vis[range];
pair<int,int>p[range];
int digui(vector<int>h,int k)
{
if(k==0)return shenxia;
vector<int>w;
// for(auto j:h)
// {
// cout<<j<<" ";
// }
// cout<<endl;
if(shenxia==2){if(k)return 0;}
if(shenxia==3)
{
if(k>=2)return 0;
else return 1;
}
for(auto i:h)
{
if(vis[i])continue;
for(auto j:v[i])
{
w.push_back(j);
}
vis[i]=1;
shenxia--;
}
return digui(w,k-1);
}
void init()
{
for(int i=1;i<=n+50;i++)v[i].clear(),vis[i]=0,cnt[i]=0;
}
void solve(int t)
{
cin>>n;
cin>>k;
for(int i=1;i<=n-1;i++)
{
cin>>x>>y;
v[x].push_back(y);
v[y].push_back(x);
cnt[x]++;cnt[y]++;
p[i].first=x;
p[i].second=y;
}
if(t==311){
cout<<n<<","<<k<<",";
for(int i=1;i<=n-1;i++)
{
cout<<p[i].first<<p[i].second<<",";
}
cout<<endl;
}
/*
1
6 2
2 5
4 3
6 2
1 5
4 5
1
6 2
1 6
4 6
2 1
3 1
1 5
*/
// return ;
// }
if(n==1||n==2){
cout<<0<<endl;
init();
return ;
}
vector<int>e;
shenxia=n;
for(int i=1;i<=n;i++)
{
if(cnt[i]==1){
e.push_back(i);
}
}
cout<< digui(e,k)<<endl;
init();
return ;
}
signed main()
{
int t ;
cin>>t;
for(int i=1;i<=t;i++)
solve(i);
}
忘了第几题
这个很简单 但是做题也启发到我一点 其实那个最终值其实和最小的ai比就行了 不用真的找出来这个值的 然后求gcd都是简单的了
困难版
这个是上面的困难版本
其实那个最终值其实和最小的ai比就行了
这句话很重要
然后做这个题的时候我当时写错了 举得例子太小了就写了个三层for循环 以为就可以选数彻底 殊不知 选的多了 这个彻底需要dfs 很明显dfs必炸 少说30的15次方你算算这个炸不炸 减枝也没用 ~~那个for循环代码在我的笔记本里 ~~
要sort的 因为理解为最小ai就是那个全相等数
下面给出正解思路 第一次for 1--n/2+1 没问题
我当时做题是一段一段计算的 比如说4有三段 6有5端
我枚举5/2段就相当一半的点都搞进去了 但是这么做 枚举选取肯定是要深搜的 for怎么可能彻底
然后下面一层就是i+1-n了 枚举所有的 这里可能会纳闷 我不是贪心的要一半点吗 我假设i=1 那么这一层我全要了呀 其实这没啥 因为我们最后只要枚举因子个数有n/2有就行了呀 我不在乎你选几个 况且对于i=1 枚举后面所有的 i=2枚举后面所有的 才不会漏解呀
然后这个答案必然出现在gcd里 我们只要找到最大的因子就行了
然后那些差为0采用合并的思想 别的没啥 不写了 好饿
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int range = 4e6 + 10;
int n;
int a[range];
int b[range];
int step;
int temp[range];
int maxn;
int maxnn;
void init()
{
for(int i=1;i<=maxnn+10;i++)temp[i]=0;
}
void solve()
{
int hs=0;
cin>>n;
map<int,int>ma;
for(int i=1;i<=n;i++)cin>>a[i],ma[a[i]]++,hs=max(hs,ma[a[i]]);
if(hs>=n/2){
cout<<"-1"<<endl;
return ;
}
sort(a+1,a+1+n);
// for(int i=1;i<=n;i++)cout<<a[i]<<" ";
// cout<<endl;
int ans=0;
//-15 13 16 22 35 48
for(int i=1;i<=n/2+1;i++)
{
int res=0;
maxn=0;
// cout<<"------"<<endl<<i<<endl;
for(int j=i+1;j<=n;j++)
{
int x=a[j]-a[i];
// cout<<x<< " ";
maxn=max(x,maxn);
//找到最大因子
if(x==0)res++;
for(int k=1;k*k<=x;k++)
{
if(x%k==0)
temp[k]++;
if(k!=x/k&&x%(x/k)==0)
temp[x/k]++;
//好煞笔 一开始写成else if
//然后还不写这个x%(x/k)==0 除非嵌套在上面那个if里
//好煞笔
}
}
// cout<<endl;
// cout<<temp[13]<<endl;
maxnn=maxn;
while(temp[maxn]+res+1<n/2&&maxn>0){
maxn--;
}
// cout<<maxn<<endl;
// cout<<temp[maxn]+res+1<<endl;
// cout<<temp[13]<<endl;
init();
ans=max(ans,maxn);
}
cout<<ans<<endl;
return ;
}
signed main() {
ios::sync_with_stdio();
cin.tie(0);
cout.tie(0);
int t;cin>>t;
while(t--)
solve();
return 0;
}
/*
1
6
48 13 22 -15 16 35
*/
//深搜时间过不去 太慢了 状态太多了
//void solve() {
// cin >> n;
// init();
// int cnt=0;
// map<int, int>ma;
// for (int i = 1; i <= n; i++) {
// cin >> a[i];
// ma[a[i]]++;
// cnt=max(ma[a[i]],cnt);
// }
// sort(a+1,a+1+n);
// if(cnt>=n/2){
// cout<<"-1"<<endl;
// return ;
// }
// step = 0;
//// for (int i = 1; i <= n - 1; i++) {
//// b[++step] = (a[i + 1] - a[i]);
//// }
//// sort(b+1,b+1+step);
//// for(int i=1;i<=step;i++)
//// cout<<b[i]<<" ";
//// cout<<endl;
// int maxn = 0;
// int mmaxn=0;
//// int xuanqu = step / 2;
// int xuanqu = n / 2;
// b[0]=0;
// int zaixuan=xuanqu-1;
// cout<<zaixuan<<" "<<xuanqu<<endl;
//// for (int i = 1; i <= n - xuanqu + 1; i++) {
//// for (int j = i+1 ; j <= n-zaixuan+1; j++) {
//// maxn=a[j]-a[i];
//// for (int k = 1; k <= zaixuan-1; k++) {
//// maxn = __gcd(maxn,a[j+k]-a[j+k-1]);
//// }
//// mmaxn=max(maxn,mmaxn);
//// }
//// }
// cout<<mmaxn<<endl;
// return ;
//}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号