做题小结2

第一个题目

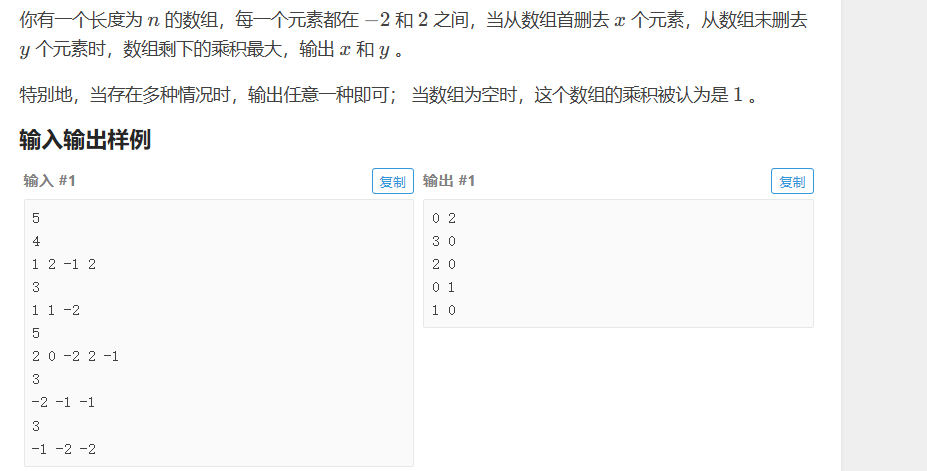
这题是真麻烦调起来
不过还好写的时候思路清晰明白了要分段做碰到0或者到头了就需要返回然后就是记录一个答案
需要求出前面的头指针此时下标然后要明白返回的l r 之间要记录是二者的距离这样方便求二者的下标别的就没啥了思路正确做起来还是蛮快的就是调的难受

node check() {
	int l = 0;	int r = 0;
	node  x;	int num = 0;	int  two = 0;
	int temp = 0;	int temptemp = 0;
	for (int i = 1; i <= step; i++) {
		if (b[i] < 0) {
			if (!l)l = i;
			r = i;
			num++;
		}
	}
	if (l == r && num == 1) {
		for (int i = l + 1; i <= step; i++)
			if (b[i] == 2)two++;了
		for (int i = 1; i <= l - 1; i++)
			if (b[i] == 2)temp++;
		if (temp > two) {
			x.ans = temp;
			x.l = 1;
			x.r = l - 1;			
		}
		else {
			x.ans = two;
			x.l = l + 1;
			x.r = step;
		}
		return x;
	} 
	else if (num % 2) {
		for (int i = 1; i <= l - 1; i++)     if (abs(b[i]) == 2)temp++;
		for (int i = r + 1; i <= step; i++)	 if (abs(b[i]) == 2)temptemp++;
		for (int i = l + 1; i <= r - 1; i++)	if (abs(b[i]) == 2)two++;
		int g = 0;
		g = two + temp + ((b[l] == -2) ? 1 : 0);
		int gg = 0;
		gg = two + temptemp + ((b[r] == -2) ? 1 : 0);
		if (g > gg) {
			x.ans = g;
			x.l = 1;
			x.r = r - 1;
		} else {
			x.ans = gg;
			x.l = l + 1;
			x.r = step;
		}
		return x;
	}
	else {
		for (int i = 1; i <= step; i++)
			if (b[i] == 2 || b[i] == -2)two++;
		x.ans = two;
		x.l = 1;
		x.r = step;
		return x;
	}
}

第二个题目

这题一开始想麻烦了开成3n*3n 后面才意识到左右循环算一次就行了反正答案是一样的你想想左移1位不就是右移动n-1位吗可以一次性算两个答案那么上下也是同理

然后记录答案我想了半天对角线如何o1求后面还是看了题解才明白人家用的前缀和用最没有逻辑思路i-1 j-1 去记录对角线而我还看了八皇后这些去优化最终还是没弄出来。。。。别的就没啥了

#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
const int range = 6e3 + 5;
int n;
char  a[range][range];
int sum[range][range];
int num=0;
void st() {
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= n; j++)
		{
		    cin >> a[i][j];	
			if(a[i][j]=='1')num++;
		}
	for (int i = 1; i <=  n; i++) {
		for (int j =  n + 1; j <= 2 * n; j++)
			a[i][j] = a[i][j - n];
	}
	for (int i = n + 1; i <= 2 * n; i++) {
		for (int j = 1; j <= n; j++)a[i][j] = a[i - n][j];
		for (int j = n + 1; j <= 2 * n; j++)a[i][j] = a[i][j - n];
	}
}
//会有很多浪费 但懒得优化了 如果跑不过 我就优化下
//我是笨比 一开始开的3n 越做越不对劲 于是2n 因为左移右移方案一样的
//int check(int x, int y, int xx, int yy) {
//	int num = 0;
//	for (int i = x; i <= xx; i++) {
//		for (int j = y; j <= yy; j++) {
//			if (i == j) {
//				if (a[i][j] == 0)num++;
//			} else {
//				if (a[i][j] == 1)num++;
//			}
//		}
//	}	ans = min(check(i - n + 1, j - n + 1, i, j), ans);
//	return num;
//}
void solve() {
	cin >> n;
	num=0;
	st();
//	for(int i=1;i<=2*n;i++)
//	{
//		for(int j=1;j<=2*n;j++)
//		{
//			cout<<a[i][j]<<" ";
//		}
//		cout<<endl;
//	}
//	cout<<endl;
	
//	for (int i = 1; i <= n * 2; i++) {
//		for (int j = 1; j <= n * 2; j++) {
//			sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j];
//		}
//	}复习二位前缀和 与二维前缀m类型
	int ans = 1e9;
	for (int i = 1; i <= 2 * n; i++) {
		for (int j = 1; j <= 2 * n; j++) {
			sum[i][j]=sum[i-1][j-1]+(a[i][j]-'0');
		}
	}
//	for(int i=1;i<=2*n;i++)
//	{
//		for(int j=1;j<=2*n;j++)
//		{
//			cout<<sum[i][j]<<" ";
//		}
//		cout<<endl;
//	}
//	cout<<endl;
	//假设num为所有的1的值 sum为对角线为1的值 
	//则代价为（n-sum）+num-sum  n-sum 对角线0 后面的是遗落在外面的1
	//求对角线 我想了半天优化对角线方法 都不合适 属实是舍本逐末了
	//边界就很好算了 区间dp一样求一个len  
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{	
		ans=min(ans,(n+num)-2*(sum[i+n-1][j+n-1]-sum[i-1][j-1]));	
			//别忘了减之前的！
		}
	}
	cout << ans << endl;
}

第三个

这个题目 cf的翻译简直依托看lg的明白才明白这个+-要明白何时转化两个相邻的-转化+
可能你会在想相邻怎么弄其实画几个图就能明白如果一段串出现负数那一定会有相邻的负号 +--这种就可以换咱们知道

+---这种才能抵消打个表就发现负数是3的倍数才行于是就ac了

#include<bits/stdc++.h>
#define int long long 
#define endl '\n'
using namespace std;
const int range=2e5+10;
int n;
string s;
int sum[range]; 
void solve()
{
	cin>>n;
	cin>>s;
	s=' '+s;
	for(int i=1;i<=n;i++)
	{
		if(s[i]=='+')sum[i]=sum[i-1]+1;
		else sum[i]=sum[i-1]-1;
	}
	int num=0;
	for(int i=1;i<=n;i++)
	{
		for(int j=i;j<=n;j++)
		{
			if(i==j)continue;
			if(sum[j]-sum[i-1]>0)continue;
			else if(sum[j]-sum[i-1]==0)num++;
			else {
				if(abs(sum[j]-sum[i-1])%3==0)num++;
			}
			// cout<<sum[j]-sum[i-1]<<" "<<i<<" "<<j<<endl;
		}
	}
	cout<<num<<endl;
	//-+---
	//1 3 
	// 1 5 
	// 2 4 
	//3 
//	if(sum[j]-sum[i-1]==0)num++;
//			else {
//				if(abs(sum[j]-sum[i-1])%4==0)num++;
//			}
}

}