做题小结-有需要重做的字符串线性dp

做题写了几个有意思的题目

第一个
题目

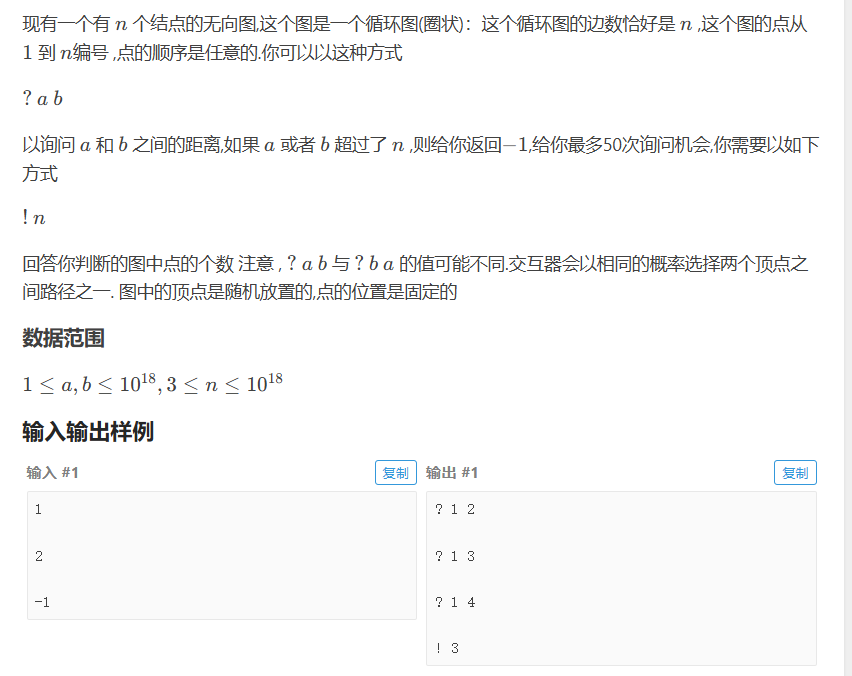
这个是一道交互题目

考察的重点是仔细审题，要注意到ab ba不同

于是一个环的长度可以通过这个询问得出 ，然后这个july陪审50次 大大降低了出错概率 。

学到的就是 问反向问 正向问起点 得到的是环的长度 即n个顶点

int check(int a, int b) {
	cout << "?" <<" "<< a << " " << b << endl;
	fflush(stdout);
	cin >> n;
	return n;
}
void solve() {
	for (int i = 2; i <= 26; i++) {
		int h = check(1, i);
		int s = check(i, 1);
		if (h == -1 ) {
			cout << "!" << " " << i - 1 << endl;
			fflush(stdout);
			return ;
		}
		if (h != s) {
			cout << "!" << " " << h + s << endl;
			fflush(stdout);
			return ;
		}
		
	}
}

第二个题

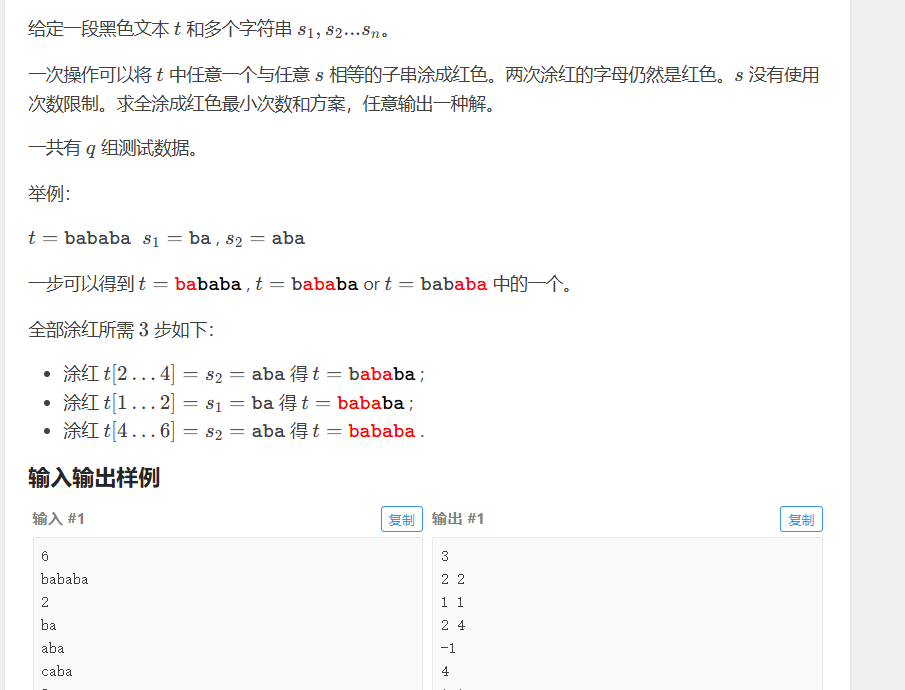
这题也更有难度，考察了字符串dp，我一开始还在想kmp啥的
但是kmp确实不太行，

数据范围很小 我也考虑了暴力，但是dp还写不来，还有这个前驱记录 我也用的不是很熟 就是dp配合这个前驱我是真的很烂

这个题 有必要多看多去重新做 字符串线性dp好题

做法其实没什么 每次匹配到就从前面开始dp找到一个覆盖点 让dp0=0 就行了
别的没啥了 我也不想多说 希望重做更有收获

我当时 很疑惑一个

abacxxxx
aba
bac

这种怎么找到的 原来枚举到第四个时它会更新到第三个a 于是我们就明白了 他是在aba的基础上覆盖的
别的就没什么了 希望重做

string  t[range];
string s;
int dp[range];
int prefix[range];
pair<int, int>p[range];
void solve() {
	cin >> s;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> t[i];
	}
	int len = s.size();
	s = ' ' + s;
	dp[0] = 0;
	for (int i = 1; i <= len; i++)dp[i] = 1e8;
	for (int i = 1; i <= len; i++) {
		for (int j = 1; j <= n; j++) {
			if (i >= t[j].size()) {
				string temp = s.substr(i - t[j].size() + 1, t[j].size());				
				if (temp == t[j]) {
					for (int k = i - t[j].size() ; k < i; k++) {
						if (dp[k] + 1 < dp[i]) {
							dp[i] = dp[k] + 1;
							p[i].first = i-t[j].size()+ 1;
							p[i].second = j;
							prefix[i] = k;;
						}
					}
				} else continue;
			}
		}
	}
	if (dp[len] == 1e8) {
		cout << -1 << endl;
		return  ;
	}
	int h = len;
	cout << dp[len] << endl;
	while (h) {
		cout << p[h].second << " " << p[h].first << endl;
		h = prefix[h];
	}
	return ;
}

第三个题目
这是我自己想出来的

我首先枚举了 0-10

于是发现了5 和0 的肯定不行 除非二者 在一块儿 然后发现了 6 2 4 8的循环

然后打了一张表 讨论他们到循环所需加的和 发现了6+20k 。
16+20k的不同答案

于是我们可以预处理

别的就没啥了 上一个图吧

CF stress 可以测代码