牛客周赛40补题--小红的矩阵划分-洛谷题解转移

很好的一道题

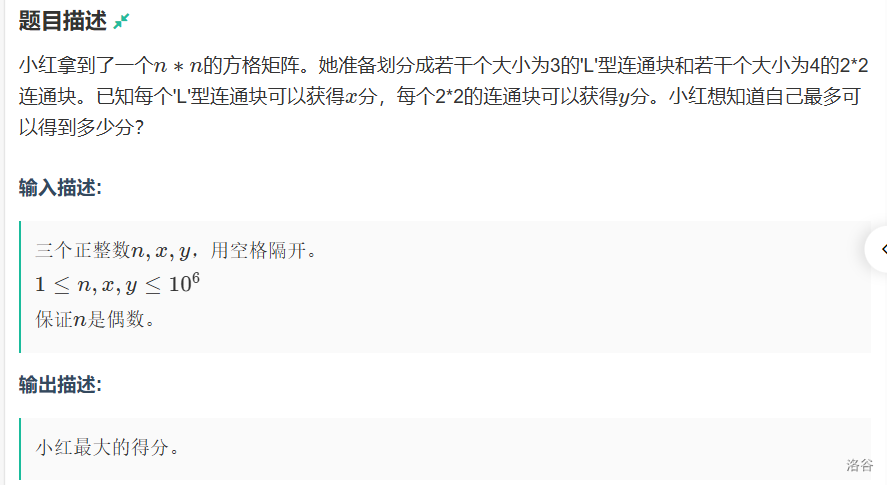
首先结论先放出来

对于n是3的倍数的
一定不可能只放L就剩一个格子

如果不是
一定可以放L就剩一个格子

证明很简单

---

假设n+6 n是偶数

则有n那个矩阵肯定可以2*2放完 6的话 2个L就行

---

如果n是奇数 拆成n+3 3的这种矩阵

n+3是偶数 3是奇数 可以放L填满

于是你会发现n+6的矩阵有4个n+3 3的矩阵

---

于是可以证明如何大于6的矩阵都可以缩放成小于等于6的矩阵

然后直接枚举1-6 于是上面结论可与证明了

首先n=3 明显不行 5 肯定可以只剩一个格子

---

于是就好了哇，然后剩一个格子的其实可以选择少一个L多放一个2的正方形 于是可以愉快写题了

---

代码

#include<bits/stdc++.h>
#define int long long 
#define endl '\n'
using namespace std;
const int range=2e5+5;
int n;
int a[200005];
void solve()
{
	cin>>n;
	int x,y;
	cin>>x>>y;
	if(n%3==0)
	{
		cout<<max(n*n/3*x,n*n/4*y);
	}
	else {
		cout<<max(n*n/3*x,max(n*n/3*x-x+y,n*n/4*y));
	}
	
	
	
}
signed main()
{
	ios::sync_with_stdio();
	cin.tie(0);
	cout.tie(0);
	solve();
	return 0;
	
	
}