三月17到4.06 4.06后先暂停不写 还有这个时间段后的题没补
https://codeforces.com/contest/2075/problem/B

赛时没写出来 就是一个特判k=1的情况 漏了 别的取最大和即可
https://codeforces.com/contest/2075/problem/D

一道dp题 我还录制了视频讲解hh 一次操作时是2的k次方 然后每次可以对x或者y进程除2^K 下取整
那么怎么思考这个题呢 我们可以二进制进行拆 就60次的事情
我们把x y拆成二进制 他们肯定是有一个公共前缀的 那么这个前缀是要留的后面都是不要的
后面不同的数字是留不下来的 这个除2的k次方相当于左移k位
那么左移k位有几种方式呢 可以直接移k位 也可以分批次移动 比如5=2+3
他的操作代价明显比一次操作5更好的 所以可以看出其实移动就是一个01背包
题目也说了只能用一次一个k
然后说一下状态转移怎么来的
我们可以开三维来表示i x y 目前状态
最终答案就是x1=y1
然后每一次i移动 两个数都是能移的 所以
可以写dpixy=dpi-1 x-i y+代价
for (int i = 1; i <= 59; i++) {
for (int u = 0; u <= 59; u++) {
for (int v = 0; v <= 59; v++) {
dp[i & 1][u][v] = min(dp[i & 1][u][v], dp[(i & 1) ^ 1][u][v]);
if (u >= i) {
dp[i & 1][u][v] = min(dp[i & 1][u][v], dp[(i & 1) ^ 1][u - i][v] + (qpow(2, i)));
}
if (v >= i) {
dp[i & 1][u][v] = min(dp[i & 1][u][v], dp[(i & 1) ^ 1][u][v - i] + (qpow(2, i)));
}
}
}
}
for (int i = 0; i <= 59; i++) {
for (int j = 0; j <= 59; j++) {
if ((x >> i) == (y >> j)) {
ans = min(ans, dp[0][i][j]);
}
}
}
预处理下即可 这里是滚动数组写法 (i&1)^1 i=8那么结果就是9
https://codeforces.com/contest/1820/problem/B

这个题蛮有意思的 由于要右移动n次 是会造成首尾相接的 所以最大矩阵是由最大的一个全是1字串所包成的 所以需要s+=s
然后考虑答案 如果siz是一个偶数 手里模拟了下11011 可以得出 23=6
如果suz是一个奇数的 比如5 那就是 33 就行了
https://codeforces.com/contest/1816/problem/A

这个题还是很有意思的 给下标准解法 我是想枚举答案的四个方向的点 但是呢 不是对的
cout<<2<<endl;
cout<<x-1<<" "<<1<<endl;
cout<<x<<" "<<y<<endl;
先跑到x-1 1 是包对的 再跑 x y
https://codeforces.com/contest/1816/problem/B

观察到序列最极端的就是 1-1 -1- n- 2-n 和1-1-2-1-2-n
如果从中间走下来 我们确保他会比这两个大就行
那么如何构造使得这两个序列差值最小呢 同时又是最大值呢
反正我没做出来 我不会
我们发现要尽可能把大数放在第一行的奇数位 第二行的偶数位 而且放的数字-减去的数字 几乎差不多
于是我们可以想到 上面放2n 2n-2 的 但是减的话就 2 4 6 8 减
下面放n+1开始递增的 但是减1 3 5 这样就刚好抵消了同时满足中途下来会更大 哎哎这题还是太麻烦了 做不来
int maxn=2*n;
int mini=2;
//其实差值都一样 和都一样 唯一就是说
//比如上下方 下面总共比你小n/2-1 但是 在减这一块比你少减一个1
//减差值一样都是n/2 从
//这样总体就会大一 如果从中间下一半下来 那么答案很明显更优
//因为下面的加数再递增 上面减的数再递增
//就会造成 对比上面继续走 加更大了 减更小了
//这题如果靠自觉去做 去猜 是个黄 要证明出来 不止这么简单
for(int i=1;i<=n;i++){
if(i%2){
a[1][i]=maxn;
maxn-=2;
}
else {
a[1][i]=mini;
mini+=2;
}
}
mini=1;
maxn=n+1;
for(int i=1;i<=n;i++)
{
if(i%2){
a[2][i]=mini;
mini+=2;
}
else {
a[2][i]=maxn;
maxn+=2;
}
}
for(int i=1;i<=2;i++){
for(int j=1;j<=n;j++){
cout<<a[i][j]<<" ";
}
cout<<endl;
}
https://codeforces.com/contest/1816/problem/C


这题很好 提醒我以后要注意差分
https://codeforces.com/gym/104460/problem/B

内向树
首先它是一个有向图,它构成类似基环树的结构,有一个特点是每个点都有且只有一个出度,并且环外的节点方向指向环内。
外向树
与基环内向树相反,它有且只有一个入度(基环内向树是出度),并且并且由环指向环外
有且只有一个入度就是说没有任何有向边指向起点,即起点的入度为零。
此题数据肯定保证不可能存在有连向入度为0的点的 那么我们进行一个并查集
不过我的是启发式合并 感觉多此一举了
https://codeforces.com/contest/2090/problem/D

讲下我赛时没有写出来的思路
我是不断放模拟的 然后题解是二分取中间 我暂时不想写这个题解的思路了 心情很差
初始化2 1 3 4 5 那么第六个怎么填呢 我们先把所有数字放进set里面
然后要放的时候如果第一个数放进来(这个公式)是素数 那么 我们就放
反之 我们就弄一个很大的数字加上前缀让把他凑成素数 此时就不是放这个数字了
然后这个很大的数字 我们可以先求出目前下一个的素数是谁 然后
while (v[p] < (pre + now + i - 1) / i)p++; now就是此时这个数
然后求出来 那么我们补多少合适呢
举个例子 假设现在pre 然后素数是11 上取整得到的11 那么假设i此时5 意味着我
pre/x=10.XX 才可以上取整得到11
所以这个pre中有x和之前的pre组成
假设我刚好整除得到这个质数-1 那么我此时 w=就是i*质数-1-之前的前缀和
但是我现在不能整除! 所以临界就是w+1 即可 然后就二分set找这个数字 没找到直接用最大的数字
去填充 让他快点度过这个不是质数的一段
for (int i = 6; i <= n; i++) {
int now = *s.begin();
if (isprime[(pre + now + i - 1) / i]) {
a[i] = now;
s.erase(s.begin());
} else {
while (v[p] < (pre + now + i - 1) / i)p++;
int nex = v[p];
int x = (nex - 1) * (i) - pre + 1;
auto it = s.lower_bound(x);
if (it == s.end()) {
it--;
a[i] = *it;
s.erase(it);
} else {
a[i] = *it;
s.erase(it);
}
}
pre += a[i];
}
https://codeforces.com/contest/1797/problem/C

这题主要就是一个切比雪夫距离 他可不是曼哈顿距离

所以问一次他会出现一个正方形
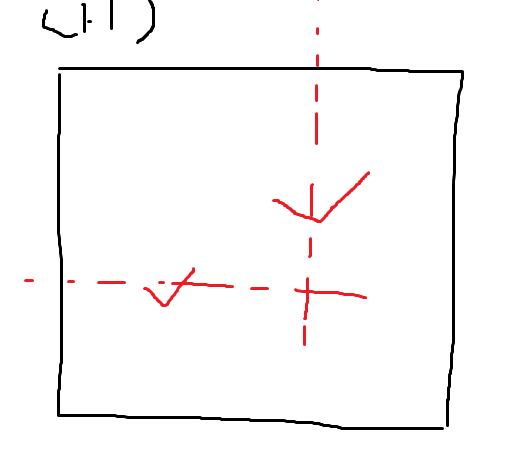
这两条打勾的边就是他的可能位置 那我再问一次 1 k+1 和k+1 1 就可以出答案了 其实这个题还和我之前做的 一个交互很像 那个题叫https://www.luogu.com.cn/problem/CF1934C


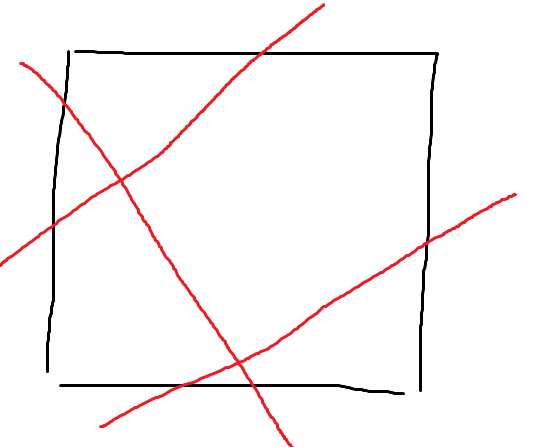
不过这一个题问法都差不多 但是要解方程 他是曼哈顿距离 但其实也是一个正方形(但是他在一条直线上的) 而不是一个圆
https://codeforces.com/contest/1805/problem/C

是一个二次函数的题
不要读错题 他只需要选出一条即可 可以重复的
直线和抛物线是否有交点取决于
我们令y=kx 和y=ax2+bx+c 联立
可以知道delta=(b-k)2-4ac要小于0
那么这个东西 其实就简单了 k是知道的 我们要尽可能选出b=k的 这样就可以小于0了 二分即可
不过也可以这样

for (int i = 1; i <= m; i++) {
cin >> a[i] >> b[i] >> c[i];
int w = 4 * a[i] * c[i];
int x = lower_bound(k + 1, k + 1 + len, b[i]) - k;
if (x != len + 1) {
if ((b[i] - k[x]) * (b[i] - k[x]) - w < 0) {
cout << "YES" << endl;
cout << k[x] << endl;
continue;
}
}
if (x != 1) {
if ((b[i] - k[x - 1]) * (b[i] - k[x - 1]) - w < 0) {
cout << "YES" << endl;
cout << k[x - 1] << endl;
continue;
}
}
cout << "NO" << endl;
}
https://codeforces.com/contest/2091/problem/F

是个dp 不过这个dp是一个前缀和的优化dp 先考虑转移吧
我们可以拆分成上下两行 与同一行之间的转移
上下两行的转移书写该怎么想呢 他转移距离范围是多少呢
题目给了一个d 如果同一行转移那么 i-d i+d 一定可以的
如果是上下 那么就y相差1 那么!! 我转移就要多考虑一个1带来的影响
那么这一行最多就只能到i+d-1了 d-1的平方+1肯定是不超过d平方的
然后我们先思考处理同行的转移吧
先初始化最后一行 X全为1 计算一个前缀和 然后我们再计算每一个点有多少个点可以来到他这一边
然后就知道每个点的同行转移pretot
pre[n][j] = ( ((pre[n][j - 1] + now[n][j])) % mod) % mod;
pretot[n][j]= (( pre[n][min(j + d, m)] - pre[n][max(j - d-1, 0 * 1LL)])+mod)%mod;
这个pretot只是求了单点的 并不能涵盖一个段内的所有总和
现在我们思考上下两行的转移
假设我在i行 那么i+1行可以转移过来的
很明显我需要快速知道我在j列 i+1有多少个点可以过来的 (这i个点也包含了同行转移到他自己的)
于是我们就需要求出一个一行的tot的前缀和 我们管他叫ans
ans[n][j] = ans[n][j - 1] + pretot[n][j];
预处理完毕
接下来
开始处理上下两行的转移
首先进行一次转移对于当前行的可行点 将上一行的所有可行答案先加上来
然后做一个前缀和 知道每个点的上下转移情况 然后再做一次前缀和 此时这个前缀和就是同行之间的转移了
最终就知道一个点包含上下同层的情况 再做一个ans的前缀和拿来存答案
for (int i = n - 1; i >= 1; i--) {
for (int j = 1; j <= m; j++) {
if (ma[i][j] == 'X') {
now[i][j] =( ans[i + 1][min(j + d-1, m)] - ans[i + 1][max(j - d+1-1, 0 * 1LL)]+mod)%mod;
// now[i][j] %= mod;
}
}
for (int j = 1; j <= m; j++) {
pre[i][j] = pre[i][j - 1] + now[i][j];
pre[i][j] %= mod;
}
for (int j = 1; j <= m; j++) {
if (ma[i][j] == 'X')
pretot[i][j] = (pre[i][min(j + d, m)] - pre[i][max(j - d-1, 0 * 1LL)]+mod) % mod;
}
for (int j = 1; j <= m; j++) {
ans[i][j] = (ans[i][j - 1] + pretot[i][j]) % mod;
}
}
https://codeforces.com/contest/1808/problem/B

拆点进行思考 我们对每一个人某一时刻的牌进行分析 能影响到他的只有同一列的别人的牌
对于这个绝对值我们可以这么想 我如果知道我排第几(这一列)那么小于我的 我都是算正的
大于我的 那我就算负的 于是我们就可以算出所有的贡献来了
for (int i = 1; i <= m; i++) {
vector<int>v;
for (int j = 1; j <= n; j++) {
v.push_back(ma[j][i]);
}
sort(v.begin(), v.end());
for (int j = 1; j <= n; j++) {
ans += (j - 1 - (n - j)) * v[j - 1];
}
}
n-j就是多少比我大的 那算的就是负贡献了
https://codeforces.com/contest/1808/problem/A

数据蛮大的 不过显然的一点是 每100次肯定会出现一次90的结尾 所以我们直接枚举分析r-l小于100
大于的直接输出90就好了
https://codeforces.com/contest/1798/problem/C

我们要尽可能的让ci都相等 bi是确定的 只能改变di
那么我们思考下di是怎么产生的呢
哎哎哎 重做想了半天还是没想清楚
下次再想想

https://codeforces.com/contest/1806/problem/C

翻译下 就是给你一个2n的数组 你要自己搞2n个数字出来 挑出n个的元素相乘等于那些没挑出来的n个元素的和 然后和题目给定数组求一个最小距离
这个题当时理解题意都想了半天 很绕 是一个结论题
只有几种可能
xx 2 2 2 2
-1-1-1....n n为偶数 奇数不满足对于任意的n序列都有
000000
然后无了
注意到n为偶数的时候这个n放最后面是最优的 而不是选一个最接近的数去放 可以画个图 我当时错了后证了下
https://codeforces.com/contest/1802/problem/C

很好的一道题 以前一直以为只有 2 3 4 5 这样的 可以异或为0
其实不是 像 1 4 3 6 也是可以的 5 8 7 10
那么偶数行和偶数列的怎么异或为0
其实他也只是2 3 4 5的变式或者0 1 2 3 的变式
2 3
512 513 不就是
2 3
0 1 每两行能产生新的2的次方就行 刚好是可以的 两行两行的产生
0 1 4 5 8 9 12 13 16 17
2 3 6 7 10 11 14 15 18 19
512 513 516 517 520 521 524 525 528 529
514 515 518 519 522 523 526 527 530 531
for (int i = 0; i < 256; i += 2) {
for (int j = 0; j < 256; j += 2) {
a[i][j] = now;
a[i][j + 1] = now + 1;
a[i + 1][j] = now + 2;
a[i + 1][j + 1] = now + 3;
now += 4;
}
}
结束!
结xiu~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号