所有DP题集合
题目

看到没有动态规划的写法,但是标签又有这个,然后题解区也没有写,所以我决定写一篇来水一下题解。
题目描述
对于一个序列 \(A_1,A_2,\cdots,A_n\),找出两个数 \(i,j\)(\(1\le i<j\le n\)),使得 \(A_j-A_i\) 最大。注意到二者下标,并不是最大减最小就是答案,对于每一个下标 \(i\),我们都要保存当前 \(i-1\) 之前遇到的最小值,然后简简单单转移即可,详见代码。
代码实现
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int range = 1e6 + 5;
int n;
int dp[range];
int a[range];
void solve() {
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
dp[0] = 1e10;
for (int i = 1; i <= n; i++)
dp[i] = min(dp[i - 1], a[i]);
int maxn = -1e10;
for (int i = 2; i <= n; i++) {
maxn = max(a[i] - dp[i - 1], maxn);
}
cout << maxn;
}
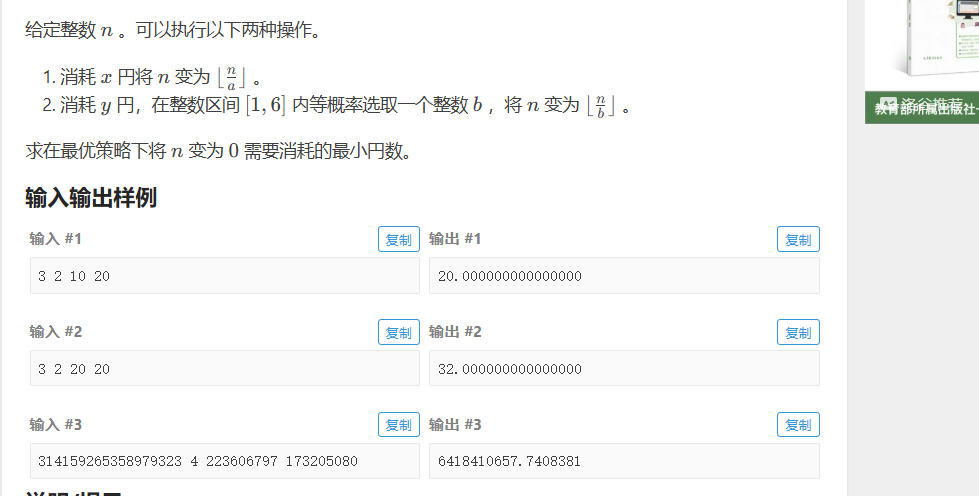
E
是一个很裸的概率dp 概率dp板子是绿
然后做概率dp 都需要推下式子 就是高中数学那种E(x)=p1f(1)+p2f(2)这种,然后这个题目 其实看到数据
需要开long long ,然后这种正推的去找答案用记忆化搜索是
很好做的,初始化答案肯定是0,记忆化搜索保存答案最常见的
就是用map来剪枝了
刚好map开1e18可以,然后我们来考虑推公式
首先对于f(n)
第一种情况就是无脑使用 支付x 变成[N/A]这种 这是显而易见的
第二种情况就是抛骰子,等概率出现1-6 P=1/6;
那么我们可以发现
f(n)=y+f(n/1)1/6+f(n/2)1/6++f(n/3)1/6+f(n/4)1/6++f(n/5)1/6+f(n/6)1/6
其中y就是代价,这个看着就跟高中写概率题一样,然后尝试化简
因为除以1就是自己本身 于是左移过去即可 1-1/6=5/6
可以得到5/6f(n)=y+f(n/2)1/6++f(n/3)1/6+f(n/4)1/6++f(n/5)1/6+f(n/6)1/6
考虑移过去5/6 得到f(n)=1.2y+1/5(f(2)+f(3)+f(4)+f(5)+f(6))
// f(n) = min(f(n/A) + X, (f(n/1)+f(n/2)+...+f(n/6))/6 + Y)
// f(n) = min(f(n/A) + X, (f(n/2)+..+f(n/6) + 6Y) / 5)
知道转移方程,然后就能写代码了 对于任何一种情况
我们对于 两种操作得到的值取min 就可以最优了
然后就没有然后了
#include<bits/stdc++.h>
typedef long long ll;
#define endl '\n'
using namespace std;
const int range=2e5+5;
ll n,a,x,y;
map<ll,double>ma;
double dfs(ll now)
{
// f(n) = min(f(n/A) + X, (f(n/1)+f(n/2)+...+f(n/6))/6 + Y)
// 第一种可以直接算,
//第二种解方程得到f(n) = (f(n/2)+..+f(n/6) + 6*Y) / 5
if(now==0)return 0;
if(ma[now])return ma[now];
//map记忆化 剪枝
double one=dfs(now/a)+x;
double two=0;
for(int i=2;i<=6;i++)
{
two+=dfs(now/i);
}
two=(two)/5.0+y*1.2;
ma[now]=min(one,two);
return ma[now];
}
void solve()
{
cin>>n>>a>>x>>y;
double ans=dfs(n);
cout<<setprecision(10)<<fixed<<ans<<endl;
}
这题也更有难度,考察了字符串dp,我一开始还在想kmp啥的
但是kmp确实不太行,
数据范围很小 我也考虑了暴力,但是dp还写不来,还有这个前驱记录 我也用的不是很熟 就是dp配合这个前驱我是真的很烂
这个题 有必要多看多去重新做 字符串线性dp好题
做法其实没什么 每次匹配到就从前面开始dp找到一个覆盖点 让dp0=0 就行了
别的没啥了 我也不想多说 希望重做更有收获
我当时 很疑惑一个
abacxxxx
aba
bac
这种怎么找到的 原来枚举到第四个时它会更新到第三个a 于是我们就明白了 他是在aba的基础上覆盖的
别的就没什么了 希望重做
string t[range];
string s;
int dp[range];
int prefix[range];
pair<int, int>p[range];
void solve() {
cin >> s;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> t[i];
}
int len = s.size();
s = ' ' + s;
dp[0] = 0;
for (int i = 1; i <= len; i++)dp[i] = 1e8;
for (int i = 1; i <= len; i++) {
for (int j = 1; j <= n; j++) {
if (i >= t[j].size()) {
string temp = s.substr(i - t[j].size() + 1, t[j].size());
if (temp == t[j]) {
for (int k = i - t[j].size() ; k < i; k++) {
if (dp[k] + 1 < dp[i]) {
dp[i] = dp[k] + 1;
p[i].first = i-t[j].size()+ 1;
p[i].second = j;
prefix[i] = k;;
}
}
} else continue;
}
}
}
if (dp[len] == 1e8) {
cout << -1 << endl;
return ;
}
int h = len;
cout << dp[len] << endl;
while (h) {
cout << p[h].second << " " << p[h].first << endl;
h = prefix[h];
}
return ;
}
这道题我是真想了半天 后面还是没想出来 哪知道是dp啊!!!
然后这个就很像背包了 不同的是第二层是直接枚举约数装进去 写法上也很讲究 我指的是初始化 没有初始化!只有边做边初初始化 为什么呢 因为对于所有的数而言 是取max 然后加上本身 如果一开始所有人都是 做的时候取max是啥意思! 对吧
所以我们只需要写个On\(\sqrt{n}\)的程序
sort(a + 1, a + 1 + n);
if(a[i]%j==0)
{
if(j==1)add=dp[a[i]/(a[i]/j)];
else
add=max(max(add,dp[a[i]/(a[i]/j)]),dp[a[i]/j]);
cout<<j<<" "<<add<<endl;
}
这就是为什么dpa[i]为什么后面++
for (int i = 1; i <= n; i++) {
for (int j = 1; j * j <= a[i]; j++) {
if (a[i] % j == 0) {
dp[a[i]] = max(max(dp[a[i]], dp[a[i] / (a[i] / j)]), dp[a[i] / j]);
}
}
dp[a[i]] ++;
ans = min(ans, n - dp[a[i]]);
}
但是! 时间还可以优化 联想埃氏筛 对于任何一个数 可以构成倍数的化 它只对自己的倍数产生贡献于是 我们就可以写一个ONlogN的代码
给这样一个代码
for (int i = 1; i <= 2e5 + 10; i++) {
for (int j = i + i; j <= 2e5 + 10; j += i) {
// 内层循环体
}
}
外层循环2e5 我10下面都不打了 我当时随便写的
内层分析
减1是减去初始的比如我们当i=2时 0一直加到2e5 是2e5/2
i=1:2e5/1-1
i=2:2e5/2-1
i=3:2e5/3-1
i=k:2e5/k-1
于是得出\(\sum\limits_{i=1}^n\dfrac{2e5}{i}-1\)
把2e5拖出来 里面就是一个调和级数的表达式
Hn=\(\sum\limits_{i=1}^n\dfrac{1}{k}\)=\(ln(n)+0.577\)
那个0.577直接省略
再来说下为什么老是明明是ln又变成log
\(lnx\)=\(loge^X\)=\(\dfrac{log2^x}{log2^e}\)
所以\(lnx\)=\(log2^X*loge^2\)
后面那个是常数直接不管了
所以回到上面
这个的时间复杂度就是ONlnN
然后直接变成Onlogn了 没区别的其实 对于复杂度没区别
不过埃氏筛氏是基于质数的调和级数 多一个log
回到原题
那么代码就可以动手写了 注意这里是随机给数据 所以我们必须要从1-n枚举 而不是1-n 枚举Ai 否则n个2的数据可以给我们卡的天上去
for(int i=1;i<=2e5;i++)
{
dp[i]+=cnt[i];
//cout<<dp[i]<<endl;
for(int j=i+i;j<=2e5;j+=i)
{
dp[j]=max(dp[j],dp[i]);
}
ans=max(ans,dp[i]);
}

这题4月做的 重新写了一遍
是一个线性dp的好题 噢,我昨天晚上做了一个计数dp的题目 做了很久 看题解看来一个多小时还是没看懂 于是这题被我扔了
题目
回到这里
这题要怎么写?
首先得明确知道这个只好用dp去写了
如果写呢?
注意到数据1e9 可以发现最多用30把坏钥匙 再用了都是0
我们可以发现可以用二维数组记录钥匙使用数量 进行转移即可 于是朴素得写法就是dp[2e5][30]这样就行 然后转移方程式
max:
dp[i][j]=dp[i-1][j-1]+a[i]>>j
dp[i][j]=dp[i-1][j]+a[i]>>j-k
然后就可以去做了
不过这里其实还是可以优化的 进行降维 让我们回顾一下降维的原则
为什么在01背包逆序可以做到降维呢
因为j是逆序循环的
所以dp[j]会优先于dp[j-a[i]]更新
也就是说dp[j-a[i]]就相当于dp[i-1][j-a[i]
于是就相当于dp[i-1][j-a[i]+w[i]
相当于用上一行的dp[j-w[i]]去更新dp[j]
dp[i][j]=max(dp[i-1][j],dp[i-1][j-a[i]+w[i])
dp[j]=max(dp[j],dp[j-a[i]+w[i])
好好对比下就明白了
所以我们对这个题进行降维书写
然后一定要注意到 当n>30时 我们一定要多加一句
if (i >= 30)dp[i][30]
= max(dp[i - 1][30] + 0, dp[i][30]);
为什么呢 因为你会发现 他这个30如果只是在for循环更新永远不能从dp[i-1][]30]就行更新 都是29
而在后面的那个代码
dp[i - 1][j] + (a[i] >> j) - k)
它是指此刻用的好钥匙 而我们其实是想用30多把坏的呢
for(int i=1;i<=n;i++)
{int maxn=0;int flag;
for(int j=30;j>=0;j--)
{
if(j>=1)dp[j]=max(dp[j]+(a[i]>>j)-k,dp[j-1]+(a[i]>>j));
else dp[j]=dp[0]+a[i]-k;
if(dp[j]>maxn){
maxn=dp[j];
flag=j;
}
}
}
这个题我没想到是DP
你会发现很多题 我都想不到是dp
因为我不会dp
再者是这道题真的很难 四维背包dp
这个数据很小的 应该考虑dp的
好了 让我们来思考下做法吧
首先看到一般元素我们可以思考到其中一维应该表示选取元素 在看到是倍数 想到取模对吧!
于是这个四维就诞生了
这道题真的很有意思 你会发现这种不同层之间有关联的 如何进行转移呢
官方代码给了一个很有创意的办法
下面一起讲到
我们假设第三维是选取的个数c
第四维是余数r然后为了防止初始化
对于这种多维的我以后都是从0开始的 省得产生不必要的麻烦
然后考虑转移公式
我们思考下对于i,j他来源于前一个i,j-1对吧
那么它可以怎么转移呢
第一种可能 我们可以不选
\(a_{i,j}\)这个元素 那么
转移中可以这样写
dp[i][j][c][r]=dp[i][j-1][c][r]
但是一定要注意了 对于dp[i][j][c][r]而言 他不仅仅是只由dp[i][j-1][c][r]转移过来的 比如说此时的c是2表示选了两个元素
那我们由j-1的选了2个的元素转过来了 也可以是j-1-1-1的选了两个元素转移过来 当然了这里都是一样的
所以这里是要取max处理的
我当时这里琢磨了半天
我是对代码每一个细节都不许放过的!
然后我们再思考 如果要用这个元素的
话
我们该怎么推导这个状态转移方程呢
很明显一旦选取了元素 那么注定会导致余数的改变
int t=r+\(a_{i,j}\)%k
转移方程应该是这样的
我们该思考转移前这二者的关系
dp[i][j][c+1][t]
dp[i][j-1][c][r]+\(a_{i,j}\)
对吧
很明显 我如果选了这个元素他太是这个转移过来的
然后大家肯定会想到 我们是取max的
为什么呢 而不是直接等于他呢
因为dp[i][j-1][c+1][t]可能也很大 我们还是要做一个对比的 如果很大的话就取他了
然后我们可以得出(就在我写这话的时候我还是错误的理解,突然开窍了,也可以看出我做这个题也不是全懂的 这也是写题解的好处)
这个c是表示整行的选取!表示本行已经选取了c个元素了,不是这个人做第c个选取(这个人做第c个的结尾)的意思,我之前一直这么认为!
那么我们总结得出
dp[i][j][c+1][t]=max(dp[i][j-1][c][r]+\(a_{i,j}\),dp[i][j-1][c+1][t])
写错了,知道哪里吗
dp[i][j-1][c+1][t]
这里错了 为什么?
我们是说来到j的时候表示现在取了c个 但是你能不能保证之前的j-1没有取到c+1个吗 并且余数还不等于t?对吧
然后供上我的错解
我是这么随便的认为可能
整个for循环0-k-1
+\(a_{i,j}\)会导致余数重复为某个值了 实际上是不会的
\(a_{i,j}\)+x=t 那这个t是不会说
会重复的
简单证明下
(0+x)%k
(1+x)%k
....
会重复吗?不会 只是所有人都+了个x%k而已 你可以理解为整体右移动!
所以说我的理解是站不住脚的
所以这里是
dp[i][j][c+1][t]=max(dp[i][j-1][c][r]+\(a_{i,j}\),dp[i][j][c+1][t]
你以为就结束了吗?
不是的
终于写完了----单行的情况了
接下来介绍本题的trick
int newi = (j == m - 1 ? i + 1 : i);
int newj = (j == m - 1 ? 0 : j + 1);
然后在不选这个元素的时候
进行分类讨论
如果此时是最后一个元素了 j为m
那么不选的话
对于下一行的第一个元素选0个就有影响的 当然了第二个不选可以由前一个推导 所以就不用想什么我下一行的第二行怎么也不初始化下这种想法了
所以有
dp[i+1][0][0][r]=max(dp[i+1][0][0][r],dp[i][m-1][c][r])
m-1就是m的意思 只是从0开始了
然后为什么取max 就是m-1这个for循环接下来还有两层r,c嘛 我们要取最大的
然后再来考虑取的时候换行如何书写
首先
int t=(\(a_{i,j}\)+r)%k
dp[i+1][0][0][t]
dp[i][m-1][c][r]+a[i][j],dp[i+1][0][0][t]
#include <bits/stdc++.h>
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 3e5 + 10;
int n;
int m;
int k;
int a[100][100];
int dp[80][80][80][80];
//你妈的 怎么这么难 卧槽卧槽我草草草草
// 卧槽卧槽我草草草草
// 卧槽卧槽我草草草草
void solve() {
cin >> n >> m >> k;
//做dp题 日后必须从0开始读
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
cin >> a[i][j];
memset(dp, -1, sizeof dp);
dp[0][0][0][0] = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
for (int c = 0; c < m / 2 + 1; c++) {
for (int r = 0; r < k; r++) {
if (dp[i][j][c][r] == -1)continue;
int newi = (j == m - 1 ? i + 1 : i);
int newj = (j == m - 1 ? 0 : j + 1);
if (newi != i) {
dp[i + 1][0][0][r] = max(dp[i + 1][0][0][r], dp[i][m - 1][c][r]);
} else {
dp[i][j + 1][c][r] = max(dp[i][j + 1][c][r], dp[i][j][c][r]);
}
if (c <= m / 2 - 1) {
int w = (r + a[i][j]) % k;
if (newi != i) {
dp[i + 1][0][0][w] = max(dp[i + 1][0][0][w], dp[i][m - 1][c][r] + a[i][j]);
} else {
dp[i][j + 1][c + 1][w] = max(dp[i][j + 1][c + 1][w], dp[i][j][c][r] + a[i][j]);
}
}
}
}
}
}
cout << dp[n][0][0][0] << endl;
}
signed main() {
ios::sync_with_stdio();
cin.tie(0);
cout.tie(0);
solve();
return 0;
}
终于写完了 你以为就结束了吗
没有
这题还有记忆化搜索的写法
我们还要补充这题的记忆化搜索写法
记忆化写起来非常简单
真的很简单
if (x == n ) {
if(r==0)return 0;
else return -1e9;
}
这个注意返回1e9 是因为对于那些最终没有用的路线 我们不能让他认为有用 直接返回-1e9让他取不了max就行了
#include <bits/stdc++.h>
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 3e5 + 10;
int n;
int m;
int k;
int a[100][100];
int dp[80][80][80][80];
int cal(int x, int y, int c, int r) {
if (x == n ) {
if(r==0)return 0;
else return -1e9;
}
if (y == m || c == m / 2) {
return cal(x + 1, 0, 0, r);
}
if(dp[x][y][c][r]!=-1){
return dp[x][y][c][r];
}
dp[x][y][c][r]=max(cal(x,y+1,c,r),cal(x,y+1,c+1,(r+a[x][y])%k)+a[x][y]);
// debug
//cout<<dp[x][y][c][r]<<endl;
// cout<<x<<" "<<y<<" "<<c<<" "<<r<<endl;
return dp[x][y][c][r];
}
void solve() {
cin >> n >> m >> k;
memset(dp,-1,sizeof dp);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++)cin >> a[i][j];
}
cout << cal(0, 0, 0, 0);
}
signed main() {
ios::sync_with_stdio();
cin.tie(0);
cout.tie(0);
solve();
return 0;
}
别的就没什么好说的了 记忆化真是yyds
第二个题

int dp[range][range];
void solve()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=n;i++)
{
a[i+n]=a[i];
}
int maxn=0;
for(int len=3;len<=n+1;len++)
{
for(int l=1;l+len-1<=2*n;l++)
{
int r=l+len-1;
for(int k=l+1;k<r;k++)
{
dp[l][r]=max(dp[l][r],dp[l][k]+dp[k][r]+a[l]*a[k]*a[r]);
maxn=max(dp[l][r],maxn);
}
}
}
cout<<maxn<<endl;
return ;
}
7.15我在看牛客的dp 顺手写的
第三个

听雨巨讲的 这个题
做了蛮久的 对于田忌来说 他只有两个选择 要么拿最好的马
要么拿最差的马 中间的马是没用的
对于
田鸡 2 3
齐王 1 3
并不是说最大打不赢就一定上早少的 不然上面那个就是平的 所以我们其实可以观察到
这个状态方程式只跟首尾有关
dp[l][r]=max(dp[l+1][r],dp[l][r-1]分别表示选l和r的情况
所以这题实际上需要对田鸡从大到小排序 对齐王从小到大排序 这样才满足我们的想法
我测试了齐王从小到大也行 他顺序没用影响 这个排序因人而异
然后就可以做出来了
//#include <bits/stdc++.h>
//#define int long long
//#define endl '\n'
//#define debug cout<<endl<<"----------"<<endl;
//using namespace std;
//const int range = 4e3 + 10;
//int n;
//int a[range];
//int tian[range];
//int qi[range];
//int dp[range][range];
//int calc(int x,int y)
//{
// if(tian[x]>qi[y])return 200;
// else if(tian[x]==qi[y])return 0;
// else return -200;
//}
//void solve() {
// cin >> n;
// for (int i = 1; i <= n; i++)cin >> tian[i];
// for (int i = 1; i <= n; i++)cin >> qi[i];
// sort(tian + 1, tian + 1 + n);
// sort(qi + 1, qi + 1 + n);
// //92 83 71
// //85 87 74
// for (int len = 1; len <= n; len++) {
// for (int l = 1; l + len - 1 <= n; l++) {
// int r=l+len-1;
// dp[l][r]=max(dp[l+1][r]+calc(l,len),dp[l][r-1]+calc(r,len));
//// debug
//// cout<<dp[l][r]<<" "<<l<<" "<<r<<endl;
//// cout<<calc(l,len)<<" "<<calc(r,len)<<endl;
////牛魔 洛谷竟然能过
// }
// //r-l+1=n-k+1
// //k=n-len+1
// }
// cout<<dp[1][n];
//}
//signed main() {
// ios::sync_with_stdio();
// cin.tie(0);
// cout.tie(0);
// solve();
// return 0;
//
//
//}
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 4e3 + 10;
int n;
int a[range];
int tian[range];
int qi[range];
int dp[range][range];
int calc(int x,int y)
{
if(tian[x]>qi[y])return 200;
else if(tian[x]==qi[y])return 0;
else return -200;
}
void solve() {
cin >> n;
for (int i = 1; i <= n; i++)cin >> tian[i];
for (int i = 1; i <= n; i++)cin >> qi[i];
for(int i=1;i<=3100;i++)
{
for(int j=1;j<=3090;j++)dp[i][j]=-1e9;
}
sort(tian + 1, tian + 1 + n, greater<int>());
sort(qi + 1, qi + 1 + n);
for(int i=1;i<=n;i++)
{
dp[i][i]=calc(i,1);
}
// 10 3 3 2 2 1
// 10 9 9 8 7 6
for (int len = 2; len <= n; len++) {
for (int l = 1; l + len - 1 <= n; l++) {
int r=l+len-1;
// debug
// cout<<dp[l][r]<<endl;
dp[l][r]=max(dp[l][r],max(dp[l+1][r]+calc(l,len),dp[l][r-1]+calc(r,len)));
// cout<<dp[l][r]<<" "<<l<<" "<<r<<endl;
// cout<<calc(l,len)<<" "<<calc(r,len)<<endl;
// cout<<len<<" ";
}
//r-l+1=n-k+1
//k=n-len+1
}
//cout<<endl;
cout<<dp[1][n];
}
signed main() {
ios::sync_with_stdio();
cin.tie(0);
cout.tie(0);
solve();
return 0;
}
第四个

这道题蛮有意思的 我一开始的写法
是错的 只考虑了单向转移
比如说 1 5 4 5这个数据 我一开始最大是5 然后假设对1 5 转移 我认为现在差距是5-4=1
这很明显是错的 所以说我的想法有缺陷 只对了三个测试点
真正的做法 是有思维难度的
我发现现在很多题 我做的话都是只能看到狭窄的一面 不能看到全部 换句话说 不能以
上帝视角一般看透这个题目 从而做出半对或者错的思路 我打多校开最难的铜牌题也发现了这个现象 我不知道咋回事
就比如这个题来说 第二层循环直接开到-5000到5000就可以涵盖所有情况
再来说下这个dp数组的含义
dp i j i表示第几个物品 j的话指上减下的值 于是直接枚举-5000到5000即可
然后加个5010防止负数 这个j我没有捕捉到 导致没写出来
#include<bits/stdc++.h>
#define debug cout<<endl<<"--------"<<endl;
using namespace std;
const int range=1e3+10;
int n;
int up[range];
int down[range];
int dp[range][10110];
void solve()
{
cin>>n;
int sum=0;
int ssum=0;
for(int i=1;i<=n;i++)
cin>>up[i]>>down[i];
memset(dp,0x3f,sizeof dp);
int w=dp[0][0];
dp[0][0+5010]=0;
// for(int i=1;i<=n;i++)
// {
// dp[0][up[i]-down[i]+5010]=0;
// }
for(int i=1;i<=n;i++)
{
for(int j=-5000;j<=5000;j++)
{
dp[i][j+5010]=min(dp[i-1][j+(up[i]-down[i])+5010],dp[i][j+5010]);
dp[i][j+5010]=min(dp[i-1][j-(up[i]-down[i])+5010]+1,dp[i][j+5010]);
}
}
int ans=2147483647;
for(int j=5010;j<=5010*2;j++)
{
if(dp[n][j]!=w)
{
ans=min(ans,dp[n][j]);
break;
}
}
for(int j=5010;j>=0;j--)
{
if(dp[n][j]!=w)
{
ans=min(ans,dp[n][j]);
break;
}
}
cout<<ans<<endl;
return ;
}
第五个

这个题需要好好读下 意思是说有些地方有石头 尽力不去跳它
然后一看数据会发现太大了 数组根本模拟不了
即使是用map存 也存不下1e9的数据 因为st很小 其实1e9的点基本都可以走到 而且map顶多
存1e8个左右数据
这里得运用到一个数学知识 路径压缩
假设我们每次走p或者p+1。。。。。证明不来
反正是这样的 只要两个石头之间的距离大于s*t-s-t 以后的值都可以随便到
int s, t;
int m;
int a[range];
int x[range];
int b[range];
int flag[range];
int dp[range];
void solve() {
cin >> n;
cin >> s >> t >> m;
for (int i = 1; i <= m; i++) {
cin >> x[i];
}
int dis=s*t-s-t+1+10;
// cout<<dis<<endl;
sort(x+1,x+1+m);
int len=0;
if(s==t)
{
for(int i=1;i<=m;i++)
{
b[i]=(x[i]-x[i-1])%s;
len+=b[i];
flag[len]+=1;
}
b[m+1]=(n-x[m])%s;
len+=b[m+1];
}
else {
for(int i=1;i<=m;i++)
{
b[i]=min(x[i]-x[i-1],dis);
// cout<<b[i]<<endl;
len+=b[i];flag[len]=1;
}
b[m+1]=min(n-x[m],dis);
len+=b[m+1];
}
memset(dp,0x3f,sizeof dp);
dp[0]=flag[0];
for(int i=1;i<=len+11;i++)
{
for(int j=s;j<=t;j++)
{
if(i-j>=0)
dp[i]=min(dp[i-j]+flag[i],dp[i]);
}
//如果在i处我们有石子 我们要尽可能降低他
//这样就不用纠结min的问题了 如果后面i+1可以取到不包含石头的
//就会取
}
int ans=2147483647;
for(int i=len;i<=len-1+t;i++)
{
ans=min(dp[i],ans);
}
if(ans==2147483647)cout<<0<<endl;
else cout<<ans<<endl;
return ;
}
signed main() {
solve();
}
参考题目小凯的疑惑
所以这个结论蛮重要的
然后知道这个结论就简单了 路径直接压缩成100就行 然后记录下总长度
状态方程是min dp[i]=dp[i-j]+flag[i],dp[i]
然后一定要注意s=t的情况是不适用这个数学结论的 因为他只能跳s的倍数
第六个

这个题有难度的 一定要意识到我们最终可以跳0-d步
但不是说可以往回跳 于是直接枚举到某一个地方时 我是从上一步是什么跳过来的
但是请注意 并不是说对于任何一个点来说 它可以来自于上一步0-d中的任何一步 这是不可能的
再着开一维时某一个点-j得到的值最大 如果这一个点不可以从上一步走j转移过来呢 你怎么
保证上一个人是走j j-1 j+1中的一个呢 所以不可以这么理想应当
我们二维记录某一个点上次走的步数 就是i-j走了j到了i
于是转移方程就是
dp[i][j]=max(dp[i-(j+d)][j-1],dp[i-(j+d)][j+1],dp[i-(j+d])[j],dp[i][j])
别问我为什么要max dp[i][j] 以后写dp 一定要写上 成为习惯 虽然这个题不写也没事
然后就是一堆细节 要加400 防止负数 再然后是d+1开始循环
还有这个
bool check(int j,int d)
{
if(j<0){
return j+d>0;
}
return 1;
}
if (i-(j+d)>=0&&check(j,d))
int maxn = 0;
memset(dp, -0x3f, sizeof dp);
//一定要赋值负无穷 不然就要出错 因为对于没发到的为0就会直接转移
for (int i = 1; i <= n; i++)cin >> a[i], flag[a[i]] += 1, maxn = max(a[i], maxn);
dp[d][400] = flag[0] + flag[d];
int ans = dp[d][400];
for (int i = d + 1; i <= maxn; i++) {
for (int j = -350; j <= 350; j++) {
if (i - (j + d) >= 0 && check(j, d)) {
dp[i][j + 400] = max( dp[i - (j + d)][j + 400] + flag[i], max(dp[i - (d + j)][400 + j - 1] + flag[i], dp[i - (d + j)][400 + j + 1] + flag[i]));
if (dp[i][j + 400] > ans) {
ans = dp[i][j + 400];
// cout<<dp[i][j+400]<<" "<<i<<" "<<j<<" "<<i-(j+d)<<endl;
//cout<<dp[i-(j+d)][400+j+1]<<" "<<dp[i-(j+d)][400+j-1]<<" "<<dp[i-(j+d)][400+j]<<endl;
}
}
else continue;
}
}
第九题

这是树的最小支配 是模板题了
但是挺难的
对于儿子与父亲有三种关系
父亲选 儿子随便
父亲不选 靠儿子
父亲不选 靠爷爷
应该开dp[i][3]表示
对于父亲选的话 初始值是1
转移方程式
dp[i][1]+=min(dp[j][1],dp[j][2],dp[j][3])
对应儿子的选 不选三个情况
dp[i][3]+=min(dp[j][1],dp[j][2])
对于dp[i][2]最麻烦了
父亲不选 靠儿子 儿子就必须要选一个
那是不是说 我只需要选一个mini的dp[j][1]?
不是的
dp[j][1]:89 10
dp[j][2]:88 6
这种情况如果我们选10+88 显然不是最优的 最优的应该是
89+6
所以对于我们全选dp[j][2]的时候 不存在选dp[j][1]的情况
我们需要让其中一个dp[j][2]变成dp[j][1] 这个就是inc了
如果我们已经选了dp[j][1]那就无所谓了
那么这个inc怎么处理呢 很简单
inc=min(inc,dp[j][1]-dp[j][2])
如果成负数就证明了 肯定选了dp[j][1] 如果是正数 选最小的即可
于是
dp[i][2]+=min(dp[j][1],dp[j][2]);
if(inc)dp[i][2]+=inc;
对于dp[i][2]初始值是0
然后这题就写完了
第十题

这题有意思
其实树形dp结合背包来考是很正常的
这道题设立dp数组 不要想多开一维状态表示这个枝条有没有被剪
这个dp数组
dp[i][j]表示i这个点还剩多少个枝条
联想背包 j就像体积一样
那这个转移方程式该怎么思考呢
很明显j可以枚举0-Q
然后又由于他有很多个儿子 (假设题目变成多叉)
我们就得思考到 对一个儿子k而言
可以选多少个呢 假设父亲选了j个体积 分配到儿子的体积又是多少呢
很明显是j-父亲 父亲连接儿子的这一个代价是1
所以是j-1
这个for循环就是k=0;k<j这样写的 于是我们就可以开始写代码了
void dfs(int x, int fa)
{
dp[x][0]=0;
for (auto v : e[x]) {
if (v == fa)continue;
dfs(v, x);
for (int j = q; j >= 0; j--) {
for (int k = 0; k < j; k++) {
dp[x][j] = max(dp[x][j], dp[x][k] + dp[v][j - k - 1] + a[x][v]);
// ans = max(ans, dp[x][j]);//树枝也要算一条的
}
}
}
}
然后还有一个细节 就是我们对于j要倒着遍历为什么呢?
假设我们正着遍历 对于
dp[i][5] k=3
dp[i][5]=max(dp[i][3]....)
试想下这个dp[i][3]是哪里来的呢 这个3表示留给x自己别的儿子的 如果正着遍历 3这个状态早就被修改了 轮到5的时候 有可能这个3就是此时这个儿子的状态得来的 因为取得max啊 我们倒着就可以确保5比3早更新
第十一题

来到状态压缩的题目
啊 还有好多别的平台的题没弄呀
下午又多校
这题用的是二进制的思想 先提前预处理同一行可以放的那种情况 使用二进制就行思考 因为n比较小
比如1001 这种就可以放 1100就不行 因为互相会攻击到 于是我们可以通过预处理 处理得到在1<<n都行的那种 因为n列于是有1<<n-1种二进制
然后开一个num数组记录每一种方式需要几个国王
for循环需要枚举上一层所选的种类
然后a>>1&b!=1 a&b!=1 a<<1&b!=1
肯定还有就是体积这一块了 肯定也是要for循环枚举的
还有就是num[a]<=j
最终转移方程式就是
dp[i][j][a]+=dp[i-1][j-num[a][b]
表示以a为状态 上一行以b为状态 此时可以放j个的dp方程式
然后这边要注意初始时0也要算一个可行的状态不然没法进行初始状态1 2 4这种的可行状态的dp[1][j][a]的转移 可以这么理解0就是上一行啥也没放 这也算啊
第十二题

下午多校 又是坐牢
这道题其实和上一题很像 只不过多一个状态而已 多一个上上行而已
但是少了一个q 所以我们可以试着确定dp数组
dp[i][a][b]表示此行a上一行b 于是和dp[i-1][b][c]有关
然后提前预处理同行即可 别的注意事项都很正常了 个人认为题目都很好
建议重做
第十三个

数位dp
对于数位dp一定要有dp[b]-dp[a-1]这种思想
然后考虑预处理
dp[i][j]表示i位数是j 此时若 abs(k-j)>=2就要+上dp[i-1][k]
要考虑前导0因为 我们计算答案要用到02 036.。。。这种 只需要
calc函数的时候 首位从1开始即可
然后在写calc函数一定要注意 我们计算两种情况
一种是位数小于这个a的和位数等于a的
对于位数等于a为我们只需要一位位计算 last=now不断更新即可
还要if i==1 的判断 表示a自己就是
还有很多题啊啊啊
位数小于a 直接for开始加
接上一篇博客
第一题
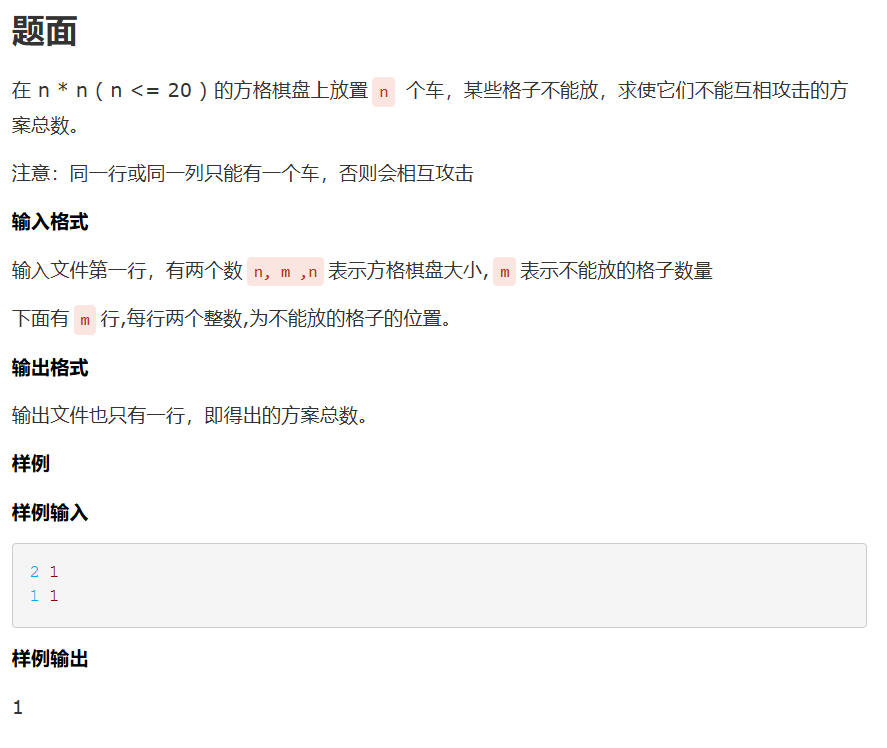
对于一列来说 只能放一个 一行也是同理 形成一个十字
又因为某些格子不能放 于是我们可以让不能放的格子如同炮兵阵地一样
不能放的位置为0
然后其实可以发现 每一行和上一行有关 可以让上一行承接之前所有
行的状态 类似一个前缀和
懒得写滚动了 反正n小
于是我们可以写出一个表达式
dp[i][j]表示第行的第j个列
对于转移方程式
如果j没有
则有dp[i][j]=max(dp[i-1][j]+1,dp[i][j]);这是错的理解!
j不能是列 j是列的话 转移状态很麻烦 某一列j是没有放的
可以放 那么这次放上了 其实我们也可以选择不放 那还要开个维[2]
表示放没放 那太麻烦了 转移起来 这也是状态压缩的出现意义
但是!!!j到底是什么呢 j是列是错的 因为是承接前面的 这个i-1行会有很多“1” 分别对应了i-1 i-2 的状态 所以这里其实就是1<<n-1种状态了 对于某一个i 1的个数不能大于i 对吧
所以这个二维你可以理解为1<<n的某种状态 而不是列
然后呢 我之前说了是承接上面的行
比如 10010101
可以由10000101的来 也可以是00010101的来所以是个+
所以这个dp转移就出来了
我们想想该如何开展循环
for(1-20)for(0-1<<20)应该是这样的 如果1的个数大于i直接continue
然后用lowbit函数进行转移
看了下代码 发现第一层循环其实不用。。加上的话我算了下
20 * 5e5 * 15 估摸可能要超时。。。。这个是往多了算。。。
好吧 直接上代码
for(int j=i;j>=1;j-=lowbit(j))
{
if((a[cnt]|lowbit(j))>a[cnt])
{
// debug
// cout<<i<<" "<<j<<" "<<lowbit(j)<<endl;
//a[cnt]&j==0
int temp=i^(lowbit(j));
dp[i]+=dp[temp];
// cout<<dp[i]<<" "<<i<<" "<<temp<<endl;
//我直接 dp[cnt]+=dp[lowbit(j)了 错了
}
}
下一个

是个区间dp 括号匹配
然后记住 像这种转移的方程是很正常的
一头一尾
dp[l][r]=dp[l+1][r],dp[l][r-1];
#include <iostream>
#include<map>
#include<algorithm>
#include<cstring>
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 3e5 + 10;
int n;
int a[range];
string s;
int dp[1000][1000];
void solve() {
while (cin >> s) {
for(int i=0;i<=s.size()+10;i++)
{
for(int j=0;j<=s.size()+10;j++)
dp[i][j]=0;
}
if (s == "end")return ;
n = s.size() ;
map<char, int>ma;
map<char, int>num;
num['('] = 1;
num['['] = 1;
num[')'] = 0;
num[']'] = 0;
ma['('] = 1;
ma[')'] = 1;
ma['['] = 2;
ma[']'] = 2;
s = ' ' + s;
int ans = 0;
for (int len = 2; len <= n; len++) {
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
for (int k = l + 1; k < r; k++) {
if (ma[s[l]] == ma[s[k]] && s[l] != s[k] && num[s[l]] == 1)
dp[l][r] = max(dp[l+1][k-1] + dp[k + 1][r] + 1, dp[l][r]);
}
if (ma[s[l]] == ma[s[r]] && s[l] != s[r] && num[s[l]] == 1)
dp[l][r] = max(dp[l+1][r-1] + 1, dp[l][r]);
dp[l][r] = max(dp[l + 1][r], max(dp[l][r - 1], dp[l][r]));
ans = max(dp[l][r], ans);
// debug
// cout << len << endl;
// cout << ans << " " << dp[l][r] << " " << l << " " << r << endl;
}
}
cout << ans * 2 << endl;
}
}
下一个
和能量项链很像这一道题 肯定是要断环为链的
然后注意二层循环肯定是要更新到l+len-1<=2n
为什么呢 比如n+1想和n+3连一块儿 也是可以的呀 所以也要更新的
然后一层循环和项链不同的是 我们只需要到n即可 而那个题是因为要计算尾巴 答案区间长度是n+1 我一开始写的是n+1
别的就没什么了 一开始固定长度为3 就行了
ICPC2023网络赛

这个题是2023网络赛的 状态压缩的dp
可以分析到dp需要存到7个状态 分别表示小写 大写 大小写
小数字 大数字 大小数字 啥都没有
其实就是000 001 011 ----111这样
那么我们该思考如何书写转移方程式呢
dp数组很明显就是dp[i][x][7]了 表示此时i个以x结尾
因为不能相邻所以弄个结尾
转移方程该如何书写呢
假设我么当前字符是小写字母 是不是之前无小写的都可以通过转移对吧
然后对于之前含有小写的意味着我们也可以把答案转移过来
我们可以认为|1就是把1带上了 |2就是把大写带上了 |4就是数字带上了
我在写这一篇题解都在口胡上次的做法 能说多少算多少
假设此时是小写 直接外面枚举一层for循环从0到7
里层是for从小写a到数字结束中间有个小写会排斥要continue
然后dp[i][x][j|1]+=dp[i-1][k][j]
然后题目说了可以当大写 没关系同样的写法再来一遍
dp[i][x][j|2]+=dp[i-1][k][j]
此时x是大写了
对于大写的话 dp[i][x][j|1]+=dp[i-1][k][j]就这样
是数字的话 dp[i][x][j|4]+=dp[i-1][k][j]就这样
如果是“?”
他可以充当任何对吧
for(int i=0-7)
for(j=0;j-62)直接枚举每一位的可能性
比如这一位是数字 那么就当数字处理了 那么此时这个的答案转移
也是开一层循环进行叠加
是小写字母 由于可以当大写 于是可以 写两个转移 如果是大写再写一个
这样程序就写完了 然后输出答案的话就是dp[n][k][7]哪个大用哪个
应该是这样的吧
卧槽 什么 前缀和 淦
用前缀和 是个好办法 我那个估摸着不会超时吧?
我算算n762*62 我多算了一层循环
我这里指的是?字符时 要计算x目前是什么 然后还要知道上一个
选的什么
因为那个累计答案 我还要考虑上一个具体选了什么 就是那个k。。。
要超时了 用前缀和确实可以诶
前缀和数组记录上一层的7个状态
然后一减去当前的同样的的就肯定是上一层的所有答案了 我去
不错不错不错。。。。 重新思考果然更有体会了
要开滚动 这没话说
总体思路没问题 就是没想起要开前缀和优化 然后对于每个状态我都提到了要开for(0-7)其实开外面 大家一起用就行了 代码更简洁
很好的一道状态压缩题!
至此 应该是所有题目整理完了 当然那些场切的 我觉得没啥的 就没写了
#include <bits/stdc++.h>
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int mod = 998244353;
const int range = 1e5 + 10;
int n;
int dp[10][70][10];
char s[range];
long long sum[10];
void solve() {
scanf("%d",&n);
scanf("%s",s+1);
dp[0][63][0] = 1;
//1 小写 2大写 3大小写 4 数字 5数字+小写 6 数字+大写 7什么都有
//j表示选的东西 此时
for (int i = 0; i <= n - 1; i++) {
for (int j = 1; j <= 63; j++)
for (int k = 0; k <= 7; k++)
dp[(i + 1) & 1][j][k] = 0;
//必须清空 不然会重叠
for (int j = 0; j <= 7; j++)
sum[j] = 0;
for (int k = 0; k <= 7; k++)
for (int j = 1; j <= 63; j++)
sum[k] += dp[i & 1][j][k], sum[k] %= mod;
for (int k = 0; k <= 7; k++) {
if (s[i + 1] == '?') {
for (int j = 1; j <= 26; j++) {
dp[(i + 1) & 1][j][k | 1] =( ((sum[k] - dp[i & 1][j][k]) % mod) + dp[(i + 1) & 1][j][k | 1]+mod)%mod;
dp[(i + 1) & 1][j][k | 1] %= mod;
//k=5 25 + 9=34
}
for (int j = 27; j <= 52; j++) {
dp[(i + 1) & 1][j][k | 2] =( ((sum[k] - dp[i & 1][j][k]) % mod) + dp[(i + 1) & 1][j][k | 2]+mod)%mod;
dp[(i + 1) & 1][j][k | 2] %= mod;
}
for (int j = 53; j <= 62; j++) {
dp[(i + 1) & 1][j][k | 4] =( ((sum[k] - dp[i & 1][j][k]) % mod) + dp[(i + 1) & 1][j][k | 4]+mod)%mod;
dp[(i + 1) & 1][j][k | 4] %= mod;
}
} else {
if (s[i + 1] >= 'a' && s[i + 1] <= 'z') {
int x = s[i + 1] - 'a' + 1;
dp[(i + 1) & 1][x][k | 1] =( ((sum[k] - dp[i & 1][x][k]) % mod) + dp[(i + 1) & 1][x][k | 1]+mod)%mod;
dp[(i + 1) & 1][x][k | 1] %= mod;
x = x + 26;
dp[(i + 1) & 1][x][k | 2] = (((sum[k] - dp[i & 1][x][k]) % mod) + dp[(i + 1) & 1][x][k | 2]+mod)%mod;
dp[(i + 1) & 1][x][k | 2] %= mod;
} else if (s[i + 1] >= 'A' && s[i + 1] <= 'Z') {
int x = s[i + 1] + 32 - 'a' + 1 + 26;
dp[(i + 1) & 1][x][k | 2] = (((sum[k] - dp[i & 1][x][k]) % mod) + dp[(i + 1) & 1][x][k | 2] +mod)% mod;
dp[(i + 1) & 1][x][k | 2] %= mod;
} else if (s[i + 1] >= '0' && s[i + 1] <= '9') {
int x = 53 + s[i + 1] - '0';
dp[(i + 1) & 1][x][k | 4] = ((((sum[k] - dp[i & 1][x][k]) + mod) % mod + dp[(i + 1) & 1][x][k | 4]+mod)) % mod;
dp[(i + 1) & 1][x][k | 4] %= mod;
}
}
}
}
int ans = 0;
for (int j = 1; j <= 62; j++) {
ans += dp[n & 1][j][7];
ans %= mod;
}
cout << ans << endl;
}
int main() {
solve();
return 0;
}
第一个

开了个二维数组表示删除不删除
然后去重了下 如果前后相差为1的话 ,就可以进行删除的思考 此时i要删除
的话 i-1必须要不删除 如果i不删除的话 存一个前面的max即可
这边注意下可能有重复的数
如果前后相差不为1的话 我们就可以肆无忌惮 怎么搞都行
此题结束
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 3e5 + 10;
int n;
int a[range];
map<int,int>ma;
int dp[range][3];
int b[range];
int cnt=0;
void solve() {
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
if(ma[a[i]]){ma[a[i]]++;continue;}
else b[++cnt]=a[i],ma[a[i]]++;
}
sort(b + 1, b +1 + cnt, greater<int>());
for (int i = 1; i <= cnt; i++) {
if (b[i - 1] - b[i] == 1) {
dp[i][0]=max(dp[i][0],max(dp[i-1][1],dp[i-1][0]));
dp[i][1]=max(dp[i][1]+(b[i]*ma[b[i]]),dp[i-1][0]+(b[i]*ma[b[i]]));
} else {
dp[i][0]=max(dp[i-1][1],dp[i-1][0]);
dp[i][1]=max(dp[i-1][1],dp[i-1][0])+(b[i]*ma[b[i]]);
}
}
cout<<max(dp[cnt][1],dp[cnt][0])<<endl;
}
第二题
这题和上一题相对比起来更难了

int dp[range][4][10];
dp[1][0][0] = 0; 不动
dp[1][1][1] = 1; //左
dp[1][1][2] = 0; //右边
我这边默认左可删的 如果在距离够的情况下 但是右边可以不可以删除取决于后面的距离够不够
dp[i][0][0] = max(max(dp[i - 1][0][0], dp[i][0][0]), max(dp[i - 1][1][1], dp[i - 1][1][2]));
if (x[i] - x[i - 1] > h[i] && x[i] - x[i - 1] <= h[i] + h[i - 1]) {
dp[i][1][1] = max(max(dp[i - 1][0][0] + 1, dp[i][1][1]), max(dp[i - 1][1][2], dp[i - 1][1][1] + 1));
} else if (x[i] - x[i - 1] > h[i] + h[i - 1]) {
dp[i][1][1] = max(max(dp[i - 1][0][0] + 1, dp[i][1][1]), max(dp[i - 1][1][2] + 1, dp[i - 1][1][1] + 1));
}
if (x[i + 1] - x[i] > h[i]) {
dp[i][1][2] = max(max(dp[i][1][2], dp[i - 1][0][0] + 1), max(dp[i - 1][1][2] + 1, dp[i - 1][1][1] + 1));
}
完整代码 逻辑很清晰
第三
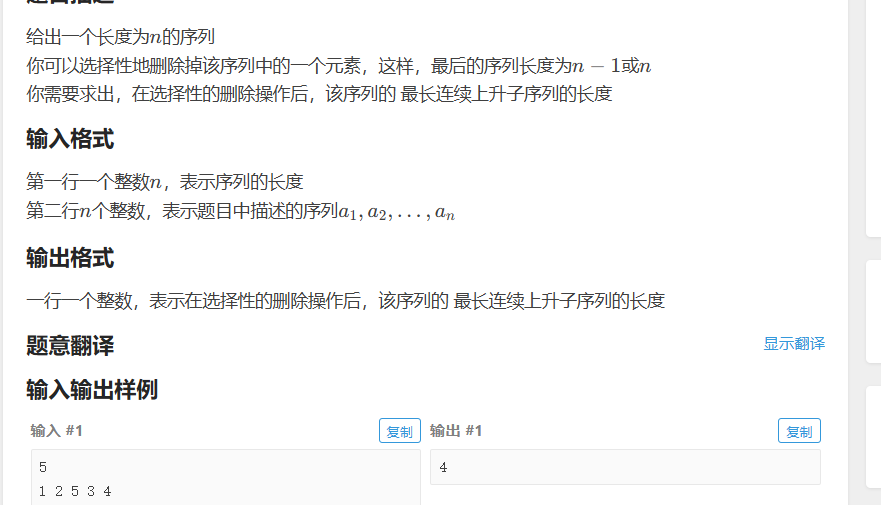
这题没做出来
我们要思考到 我们只有一次的操作机会
所以我们只能对那种中间夹了个没用的数进行删除
本来是上升的 由于这个数改变了
思考到这个就简单了 我们求一个后缀 二者拼在一块就是答案
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 3e5 + 10;
int n;
int a[range];
int dp[range];
int houzhui[range];
void solve() {
cin >> n;
int ans = 0;
for (int i = 1; i <= n; i++)cin >> a[i];
dp[1] = 1;
ans=1;
for (int i = 2; i <= n; i++) {
if (a[i - 1] < a[i]) {
dp[i] = dp[i - 1] + 1;
ans = max(ans, dp[i]);
} else dp[i] = 1;
}
houzhui[n]=1;
for (int i = n; i >= 1; i--) {
if (a[i] < a[i + 1]) {
houzhui[i] = houzhui[i + 1] + 1;
} else houzhui[i] = 1;
}
for (int i = 1; i <= n; i++) {
if ((a[i + 1] - a[i]) * (a[i + 2] - a[i + 1]) <= 0 && a[i] < a[i + 2] && i + 2 <= n) {
// debug
// cout << i << endl;
// cout << dp[i] << " " << houzhui[i + 2] << endl;
ans = max(ans, dp[i] + houzhui[i + 2]);
}
}
cout << ans << endl;
}
第四个题
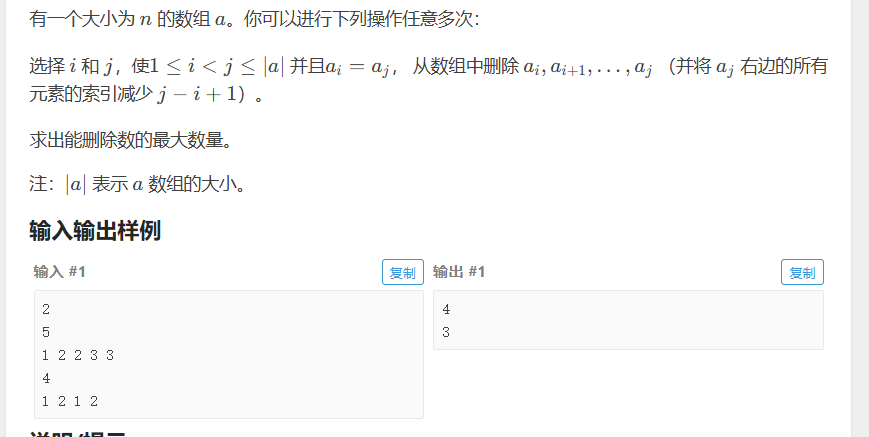
非常好的一个题
没做出来 这题蛮有意思的 真没想到
因为我没想到这个状态转移方程
fi=max(fi-1,fj-1+i-j+1)
如果暴力做 是个n方的写法
考虑优化 可以发现fj-1-j+1可以弄成一个东西
于是使用map代替下

for(int i=0;i<=n;i++)
{ dp[i]=0;cnt[i]=-1e9;}
//这题我不会
//dp[i]=dp[i-1],dp[j-1]+i-j+1
//做dp要先从n^2的情况下推转移方程 然后去优化
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)
{
dp[i]=max(dp[i-1],i+cnt[a[i]]+1);
cnt[a[i]]=max(cnt[a[i]],dp[i-1]-i);
}
cout<<dp[n]<<endl;
下一个概率dp

4 3
4 3 2 1
1 0.3
3 1
4 0.6
0.600000
很有意思的一道概率dp
我就讲正解思路了
给出这么多组操作 真正有用的其实就是第一个我们要一次到位的那个数
举个例子 4 2 1 3 5 就是那个4 能直接操作4的那个才有用
于是我们可以知道这个转移方程式就是ans=ans+(1-ans)*p
初始ans=0 我们假设第一次操作成功=p 后面就是说第一次不成功。。第二次也不成功。。。。。
很好一个题

题

这个题我的思路就是对于a分类
有两种a一个是做第一个位置的a 另一个是最后位置的
然后求一个后缀和对于第二类的a然后再for循环碰到a的话
dp[i][1] = dp[i - 1][1] + 1;
dp[i][2] = dp[i - 1][2];
dp[i][3] = max(dp[i-1][2] + asum[i],dp[i][3]);
这是b
dp[i][1] = dp[i - 1][1];
dp[i][2]=max(dp[i-1][1],dp[i-1][2])+1;
dp[i][3]=max(dp[i][2]+asum[i],dp[i][3]);
就这样了 就ac了 想的话 还好
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 3e5 + 10;
int n;
int a[range];
int dp[range][3];
string s;
int asum[range];
int bsum[range];
void solve() {
cin >> s;
n = s.size();
int ans=0;
s = ' ' + s;
for (int i = n; i >= 1; i--) {
if (s[i] == 'a')asum[i] = asum[i + 1] + 1;
else asum[i] = asum[i +1];
}
for (int i = 1; i <= n; i++) {
if (s[i] == 'a') {
dp[i][1] = dp[i - 1][1] + 1;
dp[i][2] = dp[i - 1][2];
dp[i][3] = max(dp[i-1][2] + asum[i],dp[i][3]);
} else {
dp[i][1] = dp[i - 1][1];
dp[i][2]=max(dp[i-1][1],dp[i-1][2])+1;
dp[i][3]=max(dp[i][2]+asum[i],dp[i][3]);
}
ans=max(dp[i][3],ans);
}
cout<<ans<<endl;
}
题

这是一个橙题 不过我觉得挺有意思的 很体现dp思想
对于一个正方形 我们就必须想到 一个点作为正方形的右下
那就必须满足他的左边 上面 对角 都要有值 而且这个值大家都要用 否则
无法构成正方形的 于是 状态转移就出来了 取一个min就可以了
int dp[105][105];
void solve()
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(a[i][j]==1)
{
dp[i][j]=min(dp[i-1][j],min(dp[i][j-1],dp[i-1][j-1]))+1;
ans=max(ans,dp[i][j]);
}
}
}
cout<<ans<<endl;
}
第一个

这道题考察了数论 但是很奇葩的是他只是要求前后gcd不是1就行了
所以 我们可以想到fi+1是可以直接继承fi的 如果他们俩gcd>1
然后观察了数据 这个暴力做不了的 不过牵涉到gcd不就两个做法
一个根号n的做法 求约束 另一个就是埃氏的loglog写法
本题考查后者 前者不适合 因为 我们两者如果gcd大于1 但是
数列可能不会出现我们两都有的那个约数 就无法从那个f约数进行转移了
数列给出的值完全随机呗
所以用后者就行了 对于一个ai包括他的所有质数 也就是他的约数 然后在所有的约数取一个最大值并且修改所有f值就行了 因为我们说了只要二者有gcd就可以进行继承 所以可以修改f值 然后开一个dp数组来记录最大的答案即可
for (int i = 1; i <= cnt; i++) {
for (int j = prime[i]; j <= 100005; j += prime[i]) {
v[j].push_back(prime[i]);
}
}
for (int i = 1; i <= n; i++) {
int temp = 0;
// int w=v[a[i]].size();
for (auto j : v[a[i]]) {
temp=max(temp,f[j]);
}
dp[i]=temp+1;
for(auto j:v[a[i]])
{
f[j]=max(f[j],dp[i]);
}
}
下一个

这也是一个很好的dp题 考察了离散思想
非常good 给了我新的dp建立数组的思路 因为n比较小
还有从题目推出格位这个也有的思考的 我还没想到呢
这个q是一个定值 我当时就是在想是不是
然后dp数组是这样的 dp[i][a[j]=dp[j][a[i]]+1
需要离散
哇咔咔真是好题一道
离散后的aj ai就是一个下标 刚好n很好小 于是n^2可做 同时数组也存的下 +1是因为我们每次没有包括i作为序列的尾巴
cin>>n;int ans=0;
for(int i=1;i<=n;i++)cin>>a[i];
memcpy(b,a,sizeof a);
sort(b+1,b+1+n);
int len=unique(b+1,b+1+n)-(b+1);
for(int i=1;i<=n;i++)
a[i]=lower_bound(b+1,b+1+len,a[i])-b;
for(int i=1;i<=n;i++)
{
for(int j=1;j<i;j++)
{
dp[i][a[j]]=dp[j][a[i]]+1;
ans=max(dp[i][a[j]],ans);
}
}
cout<<ans+1<<endl;
下一个dp好题

这也是一个很好的dp 我第二次看还是没发现思路出来
牵扯到一个变形
如果sumj-sumi-1=j-i+1符合式子
变形下得到sumj-j=sumi-i
于是就可以了
开一个桶记录 非常好的一个题 牵涉到一点换算 很适合我
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range=3e5+10;
int n;
int a[range];
int sum[range];
//CF93 DIV2 C
void solve()
{
cin>>n;
map<int,int>ma;
string s;
cin>>s;
s=' '+s;
for(int i=1;i<=n;i++)
{
// cin>>a[i];
int w=s[i]-'0';
a[i]=w;
}
for(int i=1;i<=n;i++){
sum[i]=sum[i-1]+a[i];
}
int ans=0;
ma[0]=1;
for(int i=1;i<=n;i++)
{
ans+=ma[sum[i]-i];
ma[sum[i]-i]++;
}
cout<<ans<<endl;
for(int i=1;i<=n;i++)sum[i]=0;
}
下一个

我当时写了一个约数还是什么的做法 反正超时了
for(int i=1;i<=n;i++)cin>>a[i],maxn=max(a[i],maxn);
sort(a+1,a+1+n);
for(int i=1;i<=n;i++)
{
for(int k=1;k*k<=a[i];k++)
{
if(a[i]%k==0)
{
v[i].push_back(k);
if(a[i]/k!=k)
v[i].push_back(a[i]/k);
}
}
}
int ans=0;
for(int i=1;i<=n;i++)
{
int w=0;
for(auto j:v[i])
{
w=max(w,dp[j]);
}
dp[a[i]]=w+1;
ans=max(ans,dp[a[i]]);
}
这题是不允许根号的 因为n=1e6 约数不行 考虑埃氏写法
于是就写出来了 采取一种A[I]只对倍数有贡献的思想 即可
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
dp[a[i]]+=1;
for(int x=2;x*a[i]<=1e6;x++)
{
// dp[x*a[i]]=dp[a[i]];写错了
dp[x*a[i]]=max(dp[a[i]],dp[x*a[i]]);
ans=max(ans,dp[x*a[i]]);
}
ans=max(ans,dp[a[i]]);
}

第一个

这道题 主要思考到一个不可以连续两步 以及最大往左移动5位 就像背包一样
所以我们开个二维的dp数组表示
for (int j = 1; j <=z ; j++) {
if (i + j *2<= k + 1 &&i-1>=1) {
dp[i][j] = max(dp[i][j - 1] + a[i - 1] + a[i], max(dp[i][j],dp[i-1][j]+a[i]));
}
}
注意到往左j步 产生回来的话就是j*2 然后这个就是一个边界条件判断
别的就没啥了 挺好的一道题目
int n;
int k;
int z;
int a[range];
int dp[range][30];
int sum[range];
void init()
{
for(int i=1;i<=n+5;i++){
for(int j=0;j<=z+5;j++)
{ a[i]=0;
dp[i][j]=0;
}
}
}
void solve() {
cin >> n >> k >> z;
for (int i = 1; i <= n; i++)cin >> a[i];
for(int i=1;i<=n;i++){
sum[i]=sum[i-1]+a[i];
}
// cout<<sum[35]<<endl;
// dp[1][0]=a[1];
for (int i = 1; i <= min(n, k + 1); i++) {
if (i <= k + 1) {
dp[i][0] = max(dp[i - 1][0] + a[i], dp[i][0]);
} else break;
// for(int j=1;j<=z;j++)
// {
// dp[i][j]=max(dp[i-1][j]+a[i],dp[i];
// }
//起始位置不算步数
for (int j = 1; j <=z ; j++) {
if (i + j *2<= k + 1 &&i-1>=1) {
// cout << i << " " << j << " " << i + j - 1 + 2 << endl;
dp[i][j] = max(dp[i][j - 1] + a[i - 1] + a[i], max(dp[i][j],dp[i-1][j]+a[i]));
}
//没有左移两次 有也没事
}
for(int j=1;j<=z;j++)
{
if(i+j*2<=k+1&&i+1<=n)
{
dp[i][j]=max(dp[i][j-1]+a[i+1]+a[i],max(dp[i][j],dp[i-1][j]+a[i]));
}
}
}
int ans = 0;
for (int i = 1; i <= min(n, k + 1); i++) {
for (int j = 0; j <= z; j++)
if (i + j == k + 1 && j == 0) {
ans = max(ans, dp[i][j]);
} else if (j > 0 && j * 2 + i == k + 1) {
ans = max(ans, dp[i][j]);
}
}init();
cout << ans << endl;
}
题目-字符串蓝题(现在是黄了)
这个题有点狗屎 要求挺多的 又要连着头尾 又要最后一样
不过我没想到最后一样这个其实不就是只输出dp[i][i]就行了
然后头尾其实就是二维表示下即可 dp[i][j]表示i开头j结尾的
然后就是一个状态转移方程
提取这个字符串的头尾
dp[i][j]=max(dp[i][j],dp[i][newt]+len)即可 这个j也是新的字符串的尾巴
然后注意dp[newt][neww]=len 记得赋值下就可以了
for(int i=1;i<=n;i++)
{
cin>>x;
int g=x[0]-'a'+1;
int gg=x[x.size()-1]-'a'+1;
int w=x.size();
for(int j=1;j<=26;j++)
{
if(dp[j][g])
dp[j][gg]=max(dp[j][gg],dp[j][g]+w);
}
dp[g][gg]=max(dp[g][gg],w);
}
for(int i=1;i<=26;i++)
{
ans=max(ans,dp[i][i]);
}
题

这个题 一开始题目读错了 后面才知道 翻转就行
我还以为是这样的操作 只能对位反转 给我思考了半天
然后其实就没什么了 四个情况 一一对应就好了 这边不列举了
int cost[range];
int a[range];
string s[range];
int dp[range][5];
string temp[range];
void solve() {
cin >> n;
for (int i = 1; i <= n; i++)cin >> cost[i];
for (int i = 1; i <= n; i++) {
cin >> s[i];
temp[i] = s[i];
reverse(temp[i].begin(), temp[i].end());
}
memset(dp, 0x3f, sizeof dp);
int ini = dp[0][0];
dp[1][0] = 0;
dp[1][1] = cost[1];
for (int i = 2; i <= n; i++) {
if (s[i] >= s[i - 1]) {
dp[i][0] = min(dp[i - 1][0], dp[i][0]);
} if (temp[i - 1] <= s[i]) {
dp[i][0] = min(dp[i - 1][1], dp[i][0]);
} if (temp[i] >= s[i - 1]) {
dp[i][1] = min(dp[i - 1][0] + cost[i], dp[i][1]);
} if (temp[i - 1] <= temp[i]) {
dp[i][1] = min(dp[i - 1][1] + cost[i], dp[i][1]);
}
}
int ans = min(dp[n][1], dp[n][0]);
if (ans == ini)cout << -1 << endl;
else
cout << min(dp[n][1], dp[n][0]) << endl;
}
树形

不错的一道好题
我写了个dfs。。。直接t飞了 我知道会t的。。。
后面思考正解 考虑dp二维表示可行不可行
反正最终答案一定是n对吧
我老是想说一件事情 就是写dp题要有一种大局观 就是上帝视角一样
有一种不拘泥小节的思想 看事情看的很远的视野
这个题就体现的很好
就像背包一样
我们开一层循环1-n 第二层表示 走到i的方式当然要取min k
其实就是个背包这个题。。。。
然后可行的就是j>=d的
状态转移
j>=d:
对于可行可以由可行与不可行转移过来
j<d
不可行呢 不可行不是说我不能从可行转移过来 那如果我之前选了d 此次我选的挺小的 就必须保存答案呀
for(int i=1;i<=n;i++)
{
for(int j=1;j<=min(k,i);j++)
{
if(j>=d)
{
dp[i][1]+=dp[i-j][0]+dp[i-j][1];
dp[i][1]%=mod;
}
else {
dp[i][1]+=dp[i-j][1];
dp[i][1]%=mod;
dp[i][0]+=dp[i-j][0];
dp[i][0]%=mod;
}
}
}
好题

for (int i = 1; i <= 1e3 + 10; i++) {
for (int j = 1; j <= i; j++) {
dp[i + i / j] = min(dp[i + i / j], dp[i] + 1);
}
}
你可以最多进行 k 次如下的操作:选择两个正整数i,x,使 ai 变成 ai+ai/x
这一步很帅 观察到n只有1000
考虑n方dp 当然你问我n大了怎么办
我也不会。。。这个dp也是很有技巧的 非常的帅
如果n大了其实你会发现到很多的j都是无用的 我想 优化的话应该要用到整除分块的思想 具体我就不知道怎么了 毕竟整除分块都是蓝模板了
跑最短路做不了的 边都建不了
然后dp写完之后 最主要还是要发现k是诈骗 实际上1e3的数据撑不了几十次 所以k多了就是浪费 所以我们太大的k直接输出就行
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 1e6 + 10;
int n;
int b[range];
int cost[range];
int dp[5000];
int k;
int ans[range];
void solve() {
//妈的 诈骗题 好坑啊 值得总结
memset(ans, 0, sizeof ans);
cin >> n >> k;
int tot = 0;
for (int i = 1; i <= n; i++)cin >> b[i];
for (int i = 1; i <= n; i++)cin >> cost[i], tot += cost[i];
//花费的价值
int sum = 0;
for (int i = 1; i <= n; i++) {
sum += dp[b[i]];
}
if (k >= sum) {
cout << tot << endl;
return ;
}
int maxn=0;
for (int i = 1; i <= n; i++) {
for (int j = k; j >= dp[b[i]]; j--) {
ans[j] = max(ans[j - dp[b[i]]] + cost[i], ans[j]);
maxn=max(maxn,ans[j]);
}
}
cout<<maxn<<endl;
// cout << ans[k] << endl;
}
signed main()
{
ios::sync_with_stdio();
cin.tie(0);
cout.tie(0);
memset(dp, 0x3f, sizeof dp);
dp[1] = 0;
for (int i = 1; i <= 1e3 + 10; i++) {
for (int j = 1; j <= i; j++) {
dp[i + i / j] = min(dp[i + i / j], dp[i] + 1);
}
}
int t;
cin >> t;
while (t--)
solve();
return 0;
}
状态压缩dp
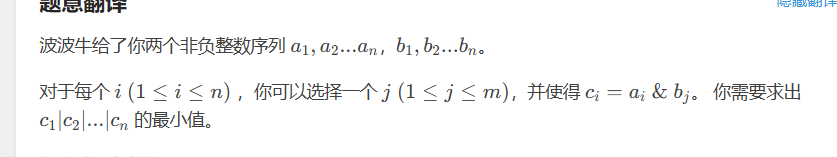
这个题 我思考错了 我也想了一个512*n的做法 不过 我后面就思考到了
还是那句话 没有全局观 其实dp数组交代不清楚
/ for (int i = 3; i <= n; i++) {
// int temp = now;
// bool flag = 0;
// for (int k = 0; k <= 520; k++) {
// if ( dp[i][k] && !flag) {
// now = k | temp;
// flag = 1;
// }
// else if (dp[i][k] && flag)
// now = min(now, k | temp);
// }
这里的dp数组是那个到i可以成多少的意思 然后就可以了
这种dp开法也是很常见的 说实话
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
int w=a[i]&b[j];
for(int k=0;k<=512;k++)
dp[i][k|w]|=dp[i-1][k];
}
}
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range=1000+10;
int n;int m;
int b[range];
int a[range];
int dp[300][range];
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=m;i++)cin>>b[i];
dp[0][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
int w=a[i]&b[j];
for(int k=0;k<=512;k++)
dp[i][k|w]|=dp[i-1][k];
}
}
for(int i=0;i<=512;i++)
{
if(dp[n][i]){
cout<<i<<endl;return ;
}
}
}
signed main()
{
ios::sync_with_stdio();
cin.tie(0);
cout.tie(0);
solve();
return 0;
}
第一个

我按dp找 结果是个二分 我还想半天 这怎么dp
不过 这题目 也很有意义
首先我一直以为vector的low或者upp下标只能用distance求
现在看来是错的 不要再写auto 迭代器写法 用int就行 减初始指针就行
然后二分的话 思路也很好
先存进去 然后在跑t的时候 先开一个指针 然后对于一个字符判断当前指针与他的下标对比 发现够用更新指针 不够用ans++ 更新指针即可
非常好的一道二分
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 3e5 + 10;
int n;
int m;
//这题一定要写题解 总结 主要我一直以为vector只能用distance
string s;
string b;
vector<int>v[30];
void solve() {
for(int i=1;i<=26;i++){
v[i].clear();
}
cin >> s;
cin >> b;
n = s.size();
m = b.size();
s = ' ' + s;
b = ' ' + b;
map<char,bool>ma;
for (int i = 1; i <= n; i++) {
int temp = s[i] - 'a' + 1;
v[temp].push_back(i);
ma[s[i]]=1;
}
for(int i=1;i<=m;i++){
if(ma[b[i]]==0){
cout<<-1<<endl;return;
}
}
int ans = 1;
int now = 0;
for (int i = 1; i <= m; i++) {
int temp = b[i] - 'a' + 1;
int it = upper_bound(v[temp].begin(), v[temp].end(), now) - v[temp].begin();
if (it >= (v[temp].size())) {
ans++;
now = v[temp][0];
continue;
} else now = v[temp][it];
}
cout << ans << endl;
}
树形dp

这是我自己想出来的 ac了感觉很开心
首先这是一颗二叉树
然后思考dp如何建立
对于一个节点而言
如果他有两个孩子 那么我们要算出他和孩子的总数
还要算出最大儿子子树的数量 还要算出如果切这个枝条那他的贡献(记住-1)
一个孩子的话 没得选
所以我们开二维表示
//0 自己子树的所有节点数
//1 表示其中某个节点的最大儿子数
//2 表示选择了一颗子树后,
//另一颗子树选了其中一颗最大子树后的值
dp[u][0]=1;
dp[u][1]=0;
dp[u][2]=0;
for(auto v:e[u])
{
if(v==fa)continue;
dfs(v,u);
dp[u][0]+=dp[v][0];
dp[u][1]=max(dp[u][1],dp[v][0]);//删的是u 不是儿子
}
下面就开始分析孩子 一个孩子的话 就只好选下去了
int w;if(u==1)w=e[u].size();
else w=e[u].size()-1;
if(w==1){
int one=0;
for(auto i:e[u]){
if(i!=fa)one =i;
}
dp[u][2]=dp[one][0]-1;
}
这边细节蛮多的
if(i!=fa)one =i;一开始没想到 后面看答案有问题才调出来
两个的
else if(w==2){
int one=0,two=0;
for(auto i:e[u]){
if(i!=fa&&!one)one=i;
else if(i!=fa&&one)two=i;
}
感觉自己太牛逼了
if(dp[one][0]+dp[two][2]>dp[two][0]+dp[one][2]){
dp[u][2]=dp[one][0]+dp[two][2]-1;
}
else {
dp[u][2]=dp[two][0]+dp[one][2]-1;
}
}
压轴登场
神题

首先给出我的思路 我开了个三维dp
二维表示此时a选的 三维表示此时b选的
发现要4个for循环吧 反正肯定要超时 然后我也没想优化
主要是脑子也没优化的概念 看了题解才知道可以优化
for (jt=1;jt<=n;jt++)
for (j2=n;j2>=jt;j2--)
for (j3=1;j3<=jt;j3++)
for (j4=max(j3,j2);j4<=n;j4++)
f[i][jt][j2]+=f[i-1][j3][j4];
那么我们该怎么优化呢 我们可以使用二维前缀和的思想
我们令sum[n][i][j]表示小于等于i 大于等于j的所有方案
那么可以怎么转移呢 很明显 我们可以由i-1 j ,i j+1 转移过来
其实二维前缀和转移 为什么j+1是因为我们毕竟算大于等于j
和j-1无关 然后你会发现重复了一段 i-1 j+1 因为二者都包含了这个
所以减去 然后呢 我们还要加上此前就有的n-1 i j 因为可以等于嘛
提前预处理1的值 后续转移要用
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=n;j>=i;j--)
{
//i是a j是b j必须大于i
e[1][i][j]=(e[1][i-1][j]+e[1][i][j+1]+mod-e[1][i-1][j+1]+1+mod)%mod;
//二维前缀和
dp[1][i][j]=1; //n=1 就不怕了
}
}
for(int i=2;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
for(int k=n;k>=j;k--)
{
//这一步很重要
dp[i][j][k]=e[i-1][j][k];
e[i][j][k]=(((e[i][j-1][k]+e[i][j][k+1])%mod-e[i][j-1][k+1]+mod)%mod+e[i-1][j][k]+mod)%mod;
要累加 所以是i
}
}
}
int ans=0;
for(int i=1;i<=n;i++){
for(int j=n;j>=i;j--){
ans=(ans+dp[m][i][j])%mod;
}
}
cout<<ans<<endl;
第二种 固定长度不下降序列的写法
可以观察到其实就是一个
写要怎么写呢
先m*2
dp数组表示第i位以j结尾
加上选j 那么j-1我们是要知道 j也是要知道
所以开一个sum记录 i-1以j结尾的 i-1以j结尾的答案 当然此时dp是等于
i-1 j-1 因为此时选的j嘛 不过sum要加上去 毕竟是前缀和
int n;int m;
int a[range];
int mod=1e9+7;
int dp[1005][1005];
int sum[1005][1005];
void solve()
{
//open my eyes in morning rain
//Clouds are slowly drifting by who is crying under the sky
cin>>n>>m;
m=2*m;
sum[0][0]=1;
int ans=0;
for(int i=1;i<=n;i++){
dp[1][i]=1;
sum[1][i]=sum[1][i-1]+1;
}
for(int i=2;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
dp[i][j]=sum[i-1][j];
//i-1以j结尾
sum[i][j]=(dp[i][j]+sum[i][j-1])%mod;
//表示i位时所有小于等于j的方案数
}
}
//跟我第一个写法好像啊 这个写法 不过更简便了
// cout<<m<<endl;
for(int i=1;i<=n;i++){
// cout<<dp[m][i]<<endl;
ans=(ans+dp[m][i])%mod;
}
cout<<ans<<endl;
}
写完了 休息下吧
第一个

这道题 我衷心觉得难的 考察递推
首先说下题目 要求你最终放慢 就是每列都要有 每一行也是 否则
那不叫满
考虑如何放置的问题 首先假设我们已经放了x个了 那么x可以由什么推来呢 x你可以理解成现在是边长为x的正方形 那么我们可以由x-1的正方形推过来 就是此时放对角线y=x 推来
然后就是难点了 还能怎么推
还有就是不放对角线 那放这两个棋子可导致直接少了两行两列 对吧
相当于从fx-2的答案推过来 然后我们又要想到此时我们有多少可以这样放的位置
首先一定要明确好这个f数组的含义 表示n边长正方形全部填满的方案数
于是就有fi-2*多少呢

我们只能在最外围那除了第一个不能放 只能放2*n-1个 你可能会问 为什么下面的3 2 这种为什么不放 注意我们这里f数组的定义 是放满n正方形! 所以只能对最外有贡献 这也是此题的难点和突破点 想清楚这个就能做出来
于是 就可以开心码了
void solve()
{
cin>>n>>k;
f[0]=1;
for(int i=1;i<=n;i++){
f[i]=f[i-1];
if(i>=2)f[i]=(f[i]+(f[i-2]*(2*i-2))%mod)%mod;
}
for(int i=1;i<=k;i++){
int x,y;cin>>x>>y;
if(x==y)n--;
else n-=2;
}
cout<<f[n]<<endl;
}
MEX好题 下一题

这题可以用最短路 去写 ONlogn的写法 也可以用ON^2的写法 也可以On的写法 神题一道了
这个题是很经典的
首先我们讲述下 思路 观察到数据范围很小
mex的概念不再细讲 求所有操作后的最小值 某一步操作谁不清楚 不确定
这种情况 一般都是这样的for循环
for(int i=1;i<=n;i++){for(int j=1;j<i;j++) do}
考虑dp方程 操作的代价可以推导出来 对于一个数 此时的mex假设是x 操作他的次数应该是cnt-1 则代价是cnt-1*x+这个数 最后一次操作mex变成这个数了
于是 dp就完整推出来了
dp[mex]=0;
for(int i=mex;i>=0;i--){
for(int j=0;j<i;j++){
dp[j]=min(dp[j],dp[i]+(ma[j]-1)*i+j);
}
}
讲下优化吧 写到这里 你一定会发现 转移的过程有太多无用的状态了
比如说 次数比你少 值也比你小 肯定先删除前者对吧
所以我们要找到这个值 从他开始 然后证明下这个复杂度吧
最坏的情况就是说 n=16 你会发现 最坏的情况就是
值从小到大排序 但是次数从大到小排序 这样的话公差为1
那有多少个数呢 一个求和公式 (n+1)*n/2=16 n是根号级别的
然后两个循环就是On的 于是优化就出来了 至少怎么优化 用栈的思想就可以了
循环从小到大 然后用cnt作为条件
给出我的写法 个人认为题解更好
stack<int>s;
s.push(0);
for(int i=1;i<=mex;i++){
if(cnt[i]>=cnt[s.top()])continue;
if(cnt[s.top()]>cnt[i])s.pop();
s.push(i);
}
mex=s.top();
题解写法
a[++top]=0;
for(int i=1;i<=mex;i++)
if(cnt[i]<cnt[a[top]])
a[++top]=i;
最后给出最短路的写法 Onlogn 神奇吧 还能最短路
我以前一直纠结于跑最短路一定要连边 没边不能跑最短路 这个题给了我例子
并不是最短路一定要连边题做得少了
我们找到mex 放进队列里 对于他访问的每一个值都连一条边 用min保存好 这样就可以更新了 每一个点都能跑比他小的点
map<int,int>ma;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
ma[a[i]]++;
}
int mex=0;
while(ma[mex])mex++;
priority_queue<node>q;
for(int i=0;i<=mex;i++)dis[i]=1e10;
q.push({mex,0});
dis[mex]=0;
while(q.size()){
int u=q.top().u;
q.pop();
for(int i=u-1;i>=0;i--){
if(dis[i]>dis[u]+(ma[i]-1)*u+i){
dis[i]=dis[u]+(ma[i]-1)*u+i;
q.push({i,dis[i]});
}
}
}
cout<<dis[0]<<endl;
最后一个题

这题不可以背包 我一开始想了半天完全背包 就是存不下 我当时想不用把他的体积一定用2^i-1 用i-1代替 比如所5就是2^5的 但是呢 这个5要怎么转移?跟背包一样写法 明确不显示2^5=32 不可以从2^3 + 2^2转移过来 于是卡壳了 写完了跑完才知道错 我也是服了
这题也充分展现了cf的人类智慧
对于一个物品的价格 他很明显可以由前面的买两个得到
如果两个的价格大于他 那就更新他的价格
然后我们要意识到可以L会远远大于这个n的 先对L拆分嘛 对于他含有1的部分 是肯定要买的 具体价格 就是前面这样定 就行了
cin>>n>>l;
cin>>a[1];
for(int i=2;i<=n;i++){
cin>>a[i];
a[i]=min(a[i-1]*2,a[i]);
}
int cnt=1;
while(l){
num[cnt++]=l%2;l/=2;
}
cnt--;
for(int i=n+1;i<=cnt;i++){
a[i]=a[i-1]*2;
}
int ans=0;
for(int i=1;i<=max(n,cnt);i++){
ans=min(ans,a[i]);
if(num[i])ans+=a[i];
}
cout<<ans<<endl;
讲下细节
while(l){
num[cnt++]=l%2;l/=2;
}
cnt--;
这一步写的非常好 求一个数的二进制 其实也是基础吧 2024.9.1更新摆烂玩金铲铲开始复健ing
ans=min(ans,a[i]);
这一步很重要 我们知道的二进制的话某位可以前面所有位相加-1
所以某一时刻ans>a[i]我们就可以更新掉
好了 写完了 中间摆烂两天 一直等手表((( 心不在焉 加油!
8.17 早
很久没写题了 大概有半个月吧 中间有许多忙事
然后这几天开学也是 手机坏掉了 电脑坏掉了 然后又要招新
最重要的是 复健 ccpc今年去不了了 因为报名没注意过时间了
第一道错排题目

做了这道题 我才知道错排的 首先错排是什么
就是说 a b c d....这么多个人 没有一个人可以站在各自的位置上
这个方案书 可以通过数学公式求出来
假设现在我们有n个元素 第n个元素放在一个位置上有n-1种放法对吧
对于这个位置k来说 这个元素k可以放在n 也可以不放 想象以下 你吃我的
我可以吃回 也可以不吃回对吧
于是有fn=(n-1)*(fn-2+fn-1) 特别的 f1=0 f2=1
下面是改编 我差点以为也是错排了
这题


第二个
当时看来一眼题目数据范围 以为dp d了半天做不出来
猜猜是什么算法

一道很好的数学dp题

这道题蛮难的
对于一个ax的拆分 他可以给前一个人的x或者y进行配对
所以有4种配对方式 我们每次都要取出最小的情况
还要考虑一个事情 就是这个拆分的数字是多少
一个数x 拆分相乘最大就是拆分的两个数字相差最小,反之,则最小
于是 我们就可以知道拆分的数字了
那么问题来了 怎么求拆分的数字 题目说了
(x-s)*(y-s)>=0 要求了 必须 两个人必须都大于或者小于s 或者至少有一个等于s
我们要对这个ax进行枚举分析
如果说这个ax很大的话 我们要拆分出极差最大的两个数 肯定是一个为s 一个为ax-s
如果ax很小的话 注意都是非负整数 两个数极差最大 肯定是一个为0 一个直接为ax了
那如果说ax恰好处于中间呢 那这个中间是什么意思呢 其实就是说大于s小于2s这种情况
这种拆分我们不能让一个数大于s 一个数小于的 这种时候想让他满足条件 我们只能让一方为s 另一方取差值 这是最优分配了 两个人都小于s 肯定不是最优的极差
于是就写出来了
for(int i=2;i<=n-1;i++){
cin>>a[i];
if(a[i]>=2*s){
mini[i]=s;maxn[i]=a[i]-s;
}
else {
mini[i]=max(0*1LL,a[i]-s);
//不可以直接定义maxn=s
maxn[i]=a[i]-mini[i];
}
}
然后注意一个dp书写 由于有4种配对方式
分别是前一个大配小大 或者前一个小配小大 于是开二维就行了
dp[i][0]=min(dp[i-1][0]+maxn[i-1]*mini[i],dp[i-1][1]+mini[i-1]*mini[i]);
dp[i][1]=min(dp[i-1][0]+maxn[i-1]*maxn[i],dp[i-1][1]+mini[i-1]*maxn[i]);
于是这题就写出来了 真有点难的
https://www.luogu.com.cn/problem/CF1829H

9.11补
DP 好题
首先一定要观察数据范围 ai的取值仅仅到63 还有k也只是6而已
如果数据打了这题就没法做了
所以我们完全可以第二维暴力存数值就行了 然后等会把第二维单独
抽出来看满足k就行了
开一个二维dp
对于任何一个ai来说 我可以继承上一个 也可以不继承
不继承那就是从他这边重新开 然后这个也可以继承之前的数值
f[i][a[i]] = 1;
f[i][j] = (1ll * f[i][j] + f[i - 1][j]) % mod;
f[i][j & a[i]] = (1ll * f[i][j & a[i]] + f[i - 1][j]) % mod;****
然后本题结束
cin>>n;cin>>k;
int ans=0;
for(int i=1;i<=n;i++){cin>>a[i];}
for(int i=1;i<=n;i++)
{
dp[i][a[i]]=1;
for(int j=0;j<=63;j++)
{
dp[i][j]=(dp[i-1][j]+dp[i][j])%mod;
// dp[i][j&a[i]]=dp[i-1][j&a[i]]+dp[i][j&a[i]]%mod;
dp[i][j&a[i]]=(dp[i-1][j]+dp[i][j&a[i]])%mod;
}
}
for(int i=0;i<=63;i++)
{ int cnt=0;
for(int j=0;j<=6;j++)
{
if(i>>j&1){
cnt++;
}
}
if(cnt==k){
ans+=dp[n][i]%mod;
}
}
for(int i=1;i<=n;i++)
{
for(int j=0;j<=63;j++)
{
dp[i][j]=0;
}
}
cout<<ans%mod<<endl;
https://www.luogu.com.cn/problem/CF1829H

DP 好题
首先一定要观察数据范围 ai的取值仅仅到63 还有k也只是6而已
如果数据打了这题就没法做了
所以我们完全可以第二维暴力存数值就行了 然后等会把第二维单独
抽出来看满足k就行了
开一个二维dp
对于任何一个ai来说 我可以继承上一个 也可以不继承
不继承那就是从他这边重新开 然后这个也可以继承之前的数值
f[i][a[i]] = 1;
f[i][j] = (1ll * f[i][j] + f[i - 1][j]) % mod;
f[i][j & a[i]] = (1ll * f[i][j & a[i]] + f[i - 1][j]) % mod;
cin>>n;cin>>k;
int ans=0;
for(int i=1;i<=n;i++){cin>>a[i];}
for(int i=1;i<=n;i++)
{
dp[i][a[i]]=1;
for(int j=0;j<=63;j++)
{
dp[i][j]=(dp[i-1][j]+dp[i][j])%mod;
// dp[i][j&a[i]]=dp[i-1][j&a[i]]+dp[i][j&a[i]]%mod;
dp[i][j&a[i]]=(dp[i-1][j]+dp[i][j&a[i]])%mod;
}
}
for(int i=0;i<=63;i++)
{ int cnt=0;
for(int j=0;j<=6;j++)
{
if(i>>j&1){
cnt++;
}
}
if(cnt==k){
ans+=dp[n][i]%mod;
}
}
for(int i=1;i<=n;i++)
{
for(int j=0;j<=63;j++)
{
dp[i][j]=0;
}
}
cout<<ans%mod<<endl;
https://www.luogu.com.cn/problem/P1130

一道橙dp 还挺有意思的 不过逻辑就那么多 没啥说的
就是题目不要理解错了 然后 注意+a[j][i]因为第i个步骤 适合新生练手
int n;int m;
int a[2005][2005];
int f[2560][2005];
void solve()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
cin>>a[i][j];
}
for(int i=1;i<=n;i++)
{
f[0][i-1]=f[m][i-1];
for(int j=1;j<=m;j++)
{
f[j][i]=min(f[j-1][i-1],f[j][i-1])+a[j][i];
}
}
// for(LL i=1;i<=n;i++){//循环n个步骤
// dp[0][i-1]=dp[m][i-1];//本题重点就在这里了!上一步的第零位,其实就是上一位的最后一位,因为最后一个小组是可以更换到1的
// for(LL j=1;j<=m;j++)//循环m个人,每一个步骤都有m个人可以完成,挨个儿决策
// dp[j][i]=min(dp[j-1][i-1],dp[j][i-1])+gay[j][i];//第i个人做第j步,可以由它的第j-1个步骤的第i-1个人或者第i个人转移过来
// }
int mini=1e8;
for(int i=1;i<=m;i++)
{
mini=min(mini,f[i][n]);
}
cout<<mini;
}
https://www.luogu.com.cn/problem/P8742

砝码称重 非常好一道题
可以两个加起来称某一个东西 也可以相减
那么代码书写 就是要前后扫一次dp 总共两次dp 我喜欢称这个为扫
然后 注意相减的那种要写成 dp[j]|=dp[j+a[i]]; 为什么呢
自己思考吧
int dp[range];
void solve()
{
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i],sum+=a[i];
dp[0]=1;
for(int i=1;i<=n;i++)
{
for(int j=sum;j>=a[i];j--)
{
dp[j]|=dp[j-a[i]];
}
}//xiangjiade
for(int i=1;i<=n;i++)
{
for(int j=1;j<=sum-a[i];j++)
{
//不能用两者相加造出来的砝码当作现有的
dp[j]|=dp[j+a[i]];
}
}
int ans=0;
for(int i=1;i<=sum;i++){
if(dp[i])ans++;
}
cout<<ans;
//
}
https://www.luogu.com.cn/problem/P1569

有点像刚才上面单调队列的前缀和问题 很像那个最大子序列
一般涉及到连续又要最大啥的 很难不dp
然后 这题 比如说 我们调了一个i就可以往前倒着找 看看最多构成几组 但是大于0的情况下
其实就是最大子序列 我都想删掉这个题了
void solve()
{
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
sum[i]=sum[i-1]+a[i];
if(sum[i]>=0)f[i]=1;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<i;j++)
{
if(f[j]>0&&sum[i]-sum[j]>=0)
{
f[i]=max(f[i],f[j]+1);
}
}
}
if(f[n]==0)cout<<"Impossible";
else cout<<f[n];
}
https://www.luogu.com.cn/problem/P1719
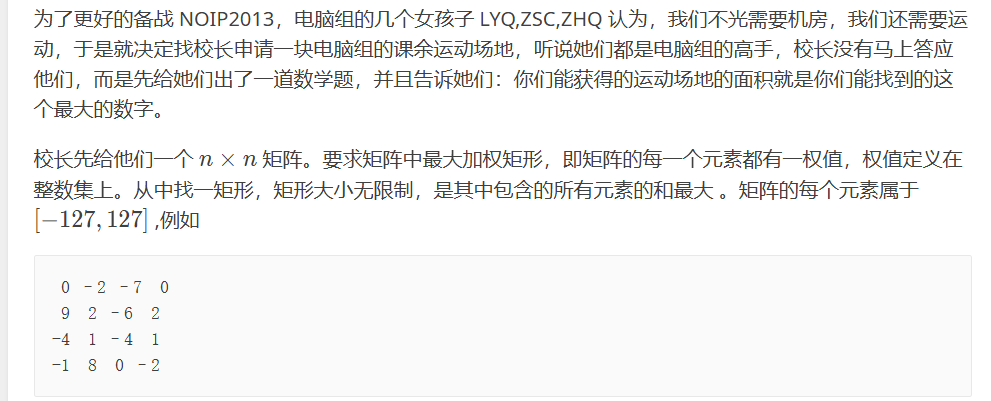
最大加权矩阵
非常好一道题 可以暴力用二位前缀和做 竟然不超时 我会讲复杂度分析
但是最关键还是要学会矩阵压缩
首先对于代码
void check() {
memset(dp, 0, sizeof dp);
for (int i = 1; i <= n; i++) {
dp[i] = max(dp[i - 1] + temp[i], dp[i]);
ans = max(ans, dp[i]);
}
}
void solve() {
for (int i = 1; i <= n; i++) {
memset(temp, 0, sizeof temp);
for (int j = i; j <= n; j++) {
for (int k = 1; k <= n; k++) {
temp[k] += a[j][k];
}
check();
}
}
}
对于solve函数 而言 注意到有三层循环
第一次 我们 会从第一行一直取到最后一行
第二次则是从第二行取到最后一行 每一次i变了 temp清空
然后temp是记载列的 不是行 注意
0 –2 –7 0
9 2 –6 2
-4 1 –4 1
-1 8 0 –2
比如 0+9 -2+2 这样的 列相加
然后我们 每次一个行的列统计完都会check一次 比如 一开始的
0 -2 -7 0
check函数里 dp[i] = max(dp[i - 1] + temp[i], dp[i]);
然后就是dpi-1如果说是小于0的 我们从第一列开始统计嘛 第一列小于0那dp1就是0
如果dp2+dp1反而小于0的 那第二列断开 默认dp2=0 dp1计入ans里去了
很灵活的
很好的模板
再来讲下On^4的做法 但是此题不会超时 数据小
for(int x1=1;x1<=n;x1++){
for(int y1=1;y1<=n;y1++){
for(int x2=1;x2<=n;x2++){
for(int y2=1;y2<=n;y2++){
if(x2<x1 || y2<y1) continue;//如果左上角比右下角还要大,就不用求了,下一个
mx=max(mx,sum[x2][y2]+sum[x1-1][y1-1]-sum[x2][y1-1]-sum[x1-1][y2]);//求最大值
}
}
}
}
分析这个复杂度才是我想说明的

等于这个
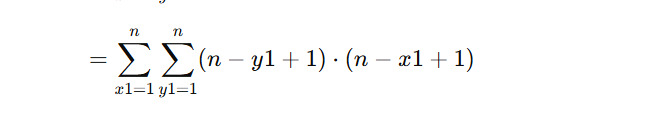
对于∑n-y1+1拆开就是


于是就是两个相乘 下面底数是4 肯定超不了的 这个复杂度计算很有意思
https://www.luogu.com.cn/problem/P1877

首先做dp一定要观察数据范围
优先考虑存数组表示 于是 转移就简单多了
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int range=2e5+5;
int n;
int beg;
int maxf;
int c[200005];
int dp[55][1005];
void solve()
{
//你可以看到我那个dp00=1
///不该这么写的 我老是忘记 dp[i][j]|=dp[i-1][j+c[i]]
//这个就是对是否取到j=0的情况呀 我老是忘
//老是以为这里j不是0 以为是c【i】
//
//切记
//切记 我老是这么认为
cin>>n;
cin>>beg>>maxf;
for(int i=1;i<=n;i++)cin>>c[i];
dp[0][beg]=1;
for(int i=1;i<=n;i++)
{
bool flag=0;
for(int j=0;j<=maxf;j++)
{
if(j>=c[i])
{
dp[i][j]|=dp[i-1][j-c[i]];//,flag=1;
}
if(j+c[i]<=maxf){
dp[i][j]|=dp[i-1][j+c[i]];//,flag=1;
}
//我这样思考还是周到 不是j+c小于就更新flag这不对
//我下面那个样例就说明了
if(dp[i][j])flag=1;
}
if(flag==0){
cout<<-1;
return ;
}
}
for(int i=maxf;i>=0;i--)
{
if(dp[n][i]){
cout<<i;
return ;
}
}
}
https://www.luogu.com.cn/problem/P9325

不可以考虑暴力做法
要体会到区间合并的概念
又大区间从小区间得到
观察以下 不难发现 5可以由3的来
4可以由2的来 于是此题做出来了

#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int range = 2e5 + 5;
int n;
int a[200005];
int h[range];
int b[range];
void solve() {
cin >> n;
for (int i = 1; i <= n; i++)cin >> h[i];
cout<<"0"<<" ";
for (int len = 2; len <= n; len++) {
int ans = 1e9;
if (len % 2 == 1) {
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
a[l] = a[l + 1] + abs(h[r] - h[l]);
ans = min(a[l], ans);
}
} else {
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
b[l] = b[l + 1] + abs(h[l] - h[r]);
ans = min(b[l], ans);
}
}
cout<<ans<<" ";
}
}
https://www.luogu.com.cn/problem/P2858

想了一下 就写出来了
观察好数据范围 发现完全可以用数组直接记录
于是考虑n n记录就行
然后 发现第t天 总共选了 多少个有两种可能
for(register int i=1;i<=n;i++)
for(register int j=0;j<=i;j++)
{
register int l=i-j;//推出右边取了多少个
dp[i][j]=max(dp[i-1][j]+in[n-l+1]*i,dp[i-1][j-1]+in[j]*i);//状态转移
//n-l+1就是从右边数第l个在in数组中的下标
}
翻到一个题解
dp[i][j]表示已经取了i个数,左边取了j个数的最优解
和我一样的思路 不过我以前做的话的思路是
for(int len=2;len<=n;len++)
{
for(int l=1;l+len-1<=n;l++)
{
int r=l+len-1;
dp[l][r]=max(dp[l+1][r]+v[l]*(n-len+1),dp[l][r-1]+v[r]*(n-len+1));
就是倒着思考了 反而是l或者r是最后才取到的意思 比如说2 - 7 我假设2是现在才取到 或者7现在才取到 我现在的思路反而不是这样的
不过没啥 没啥大区别 dp方程开对了就行
https://www.luogu.com.cn/problem/P3146

这个题不难想到区间dp 数据这么小
if(dp[l][k]==dp[k+1][r]&&>0)
对于l r 中间的值有大的尽量更新 我觉得是没后效性的 因为dp[l][r]
限定了只有l-r才有这个值 更别的也不冲突
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int range = 2e5 + 5;
int n;
int a[200005];
int dp[2004][2004];
void solve() {
cin >> n;
int ans = -1;
for (int i = 1; i <= n; i++)cin >> a[i],ans=max(a[i],ans);
for (int i = 1; i <= n; i++) dp[i][i] = a[i];
for (int len = 2; len <= n; len++) {
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
if (len == 2) {
for (int k = l; k < r; k++) {
if (dp[l][k] == dp[k + 1][r])
dp[l][r] = max(dp[l][r], dp[l][k] + 1);
ans = max(ans, dp[l][r]);
}
} else {
for (int k = l; k < r; k++) {
if (dp[l][k] == dp[k + 1][r]&&dp[l][k]!=0) {
dp[l][r] = max(dp[l][r], dp[l][k] + 1);
ans = max(ans, dp[l][r]);
}
}
}
}
}
cout<<ans<<endl;
}
https://www.luogu.com.cn/problem/P3205

首先这个题 给我的赶紧很熟悉
暑假好像做过类似的 不过不知道是不是区间dp
然后 这个题一定要搞清楚进来的顺序 以及大小
我自己打了一遍草稿才知道的
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int range=2e5+5;
const int mod=19650827;
int n;
int f[2005][2005][2];
int a[200005];
void solve()
{
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)f[i][i][0]=1;
for(int len=2;len<=n;len++)
{
for(int i=1;i+len-1<=n;i++)
{
int j=i+len-1;
if(a[i]<a[i+1])
{
f[i][j][0]+=f[i+1][j][0];
}
if(a[i]<a[j]){
f[i][j][0]+=f[i+1][j][1];
}
if(a[j]>a[j-1])
{
f[i][j][1]+=f[i][j-1][1];
}
if(a[j]>a[i]){
f[i][j][1]+=f[i][j-1][0];
//f[i][j-1][0] j在最右 i刚好弄进来 然后比不过 去了右边
}
f[i][j][0]%=mod;
f[i][j][1] %=mod;
}
}
//第i个人从左边来,他既然从左边来,
//要么第i+1人从左边来且h[i+1]>h[i];
//要么第j个人从右边来且h[j]>h[i];
//第j个人从右边来,他既然从右边来,
//要么第j-1人从右边来且h[j]>h[j-1];
//要么第i个人从左边来且h[j]>h[i];这样你i就该去右边
int hslte=(f[1][n][0]+f[1][n][1])%mod;
cout<<hslte;
}
https://www.luogu.com.cn/problem/CF1703G

首先这个题一定要意识到 他是一个折半的操作
1e9最多被操作30次 所以我么完全dp第二维可以放这个次数
然后 dp数组就开出来了 时间复杂度也就明确了
对于某一个箱子 可以使用好钥匙打开也可以不用 用坏钥匙
好钥匙打开就是
dp i j=dp[i-1][j]-k+a[i]>>j 坏钥匙 dp[i-1][j-1]+a[i]>>j
不过还需要思考到 如果我已经超过了30把钥匙的情况 dp[i][30]=max(dp[i-1][30]+0,dp[i][30]) 可能自己是第31把了
https://www.luogu.com.cn/problem/AT_abc375_e

观察数据范围 发现数据还是很小的 明显是背包类的DP 直接动手思考DP转移
第一维开N 第二维开什么好呢 注意到所有的b加起来才1500
评价没人才500 于是我们就知道了
DP N 500 500 500
但是这样会炸 mle 其实最后一个500 可以省略
还是挺有意思的 不是黄的题目 考虑的细节蛮多的 滚动数组也不行

pair<int,int>p[range];
int dp[105][range][range];
void solve()
{
cin>>n;
int sum=0;
for(int i=1;i<=n;i++)
{
int x,y;
cin>>x>>y;
p[i]={x,y};
sum+=y;
}
// cout<<sum<<endl;
if(sum%3){
cout<<-1<<endl;return ;
}
for(int i=0;i<=n;i++)
{
for(int j=0;j<=500;j++)
{
for(int k=0;k<=500;k++)dp[i][j][k]=1e14;
}
}
dp[0][0][0]=0;
//初始化非常重要 不是0的地方不能随便给0
//否则 1从0转移的时候 就会出现很多不能有的状态都给转移过来了
//比如dp[1][5][5]->dp[0][5][5]+1;
for(int i=1;i<=n;i++)
{
int x=p[i].first;
int y=p[i].second;
if(y>sum/3){
// cout<<":ssdsd"<<endl;
cout<<-1<<endl;return ;
}
for(int j=y;j<=500;j++)
{
for(int k=0;k<=500;k++)
{
dp[i][j][k]=min(dp[i][j][k],dp[i-1][j-y][k]+(x!=1));
// cout<<dp][]
}
}
for(int j=0;j<=500;j++)
{
for(int k=y;k<=500;k++)
{
dp[i][j][k]=min(dp[i][j][k],dp[i-1][j][k-y]+(x!=2));
}
}
for(int j=0;j<=500;j++)
{
for(int k=0;k<=500;k++)
{
dp[i][j][k]=min(dp[i][j][k],dp[i-1][j][k]+(x!=3));
}
}
}
if(dp[n][sum/3][sum/3]==1e14){
cout<<-1<<endl;
}
else {cout<<dp[n][sum/3][sum/3]<<endl;return ;}
https://www.luogu.com.cn/problem/CF2027C

草 实在没想到 自己现在菜的离谱了 黄题都切不出来 以前切绿就跟切菜一样。。
退役老年选手 太卑微
当时思考到了做法这些 奈何思维退化 码力变弱
第一个做法 其实就是记忆化搜索 其实改改就是一个dfs图
这个挺好的一个思路
map<int, vector<int >> ma;
map<int, int>dp;
int dfs(int x)
{
if(dp[x])return dp[x];
int ans=x;
dp[x]=ans;
for(auto i:ma[x]){
ans=max(ans,dfs(i+x));
}
dp[x]=ans;
return dp[x];
}
void solve(int t ) { //多测
cin >> n ;
dp.clear();
ma.clear();
for (int i = 1; i <= n; i++) {
cin >> a[i];
if(i==1)continue;//防止死循环
if(a[i]+i-1-n>=0)
ma[a[i] + i - 1 - n].push_back(i - 1);
}
cout<<dfs(0)+n<<endl;
第二个是 朴素写法
用set记录重复出现的 如果出现了 就把贡献加上去
(我认为的朴素写法)
set<int>s;
pair<int, int>p[range];
bool cmp(pair<int, int>x, pair<int, int>y) {
if (x.first == y.first)return x.second < y.second;
return x.first < y.first;
}
void solve(int t ) { //多测
cin >> n ;
s.clear();
for (int i = 1; i <= n; i++) {
cin >> a[i];
p[i].first = a[i] + i - 1;
p[i].second = i - 1;
}
s.insert(n);
sort(p + 1, p + 1 + n, cmp);
for (int i = 1; i <= n; i++) {
if (s.count(p[i].first)) {
s.insert(p[i].first + p[i].second);
}
}
cout << *s.rbegin() << endl;
通过这道题 也学到了东西
https://codeforces.com/contest/1903/problem/C

这个题 我二次做只能想到要倒着做了 但是还是想不清楚怎么分段
又看了代码 才知道是一个dp 还记得第一次做这个题的心情 这个题 这个怎么分块
其实不重要 我们把它理解为再加一次后缀和就行 于是这个题的状态转移就出来了
i:n->1
dp[i]max(dp[i+1]+a[i],dp[i+1]+sum+a[i])
sum+=a[i];
很好的一题
https://codeforces.com/contest/1847/problem/C

可以发现其实本题就是求最大子段异或和 01tire
介绍下dp写法 其实就是一个背包 不过这里可以优化成滚动 不过数据都是放过的
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= (1 << 8); j++) {
dp[i%2][j]=0;
}
for (int j = 0; j <= (1 << 8); j++) {
if (dp[(i - 1) % 2][j ^ a[i]]) {
dp[i % 2][j] |= dp[(i - 1) % 2][j^a[i]];
ans = max(ans, j);
}
}
dp[i % 2][a[i]] = 1;
ans = max(ans, a[i]);
}
https://codeforces.com/contest/2075/problem/D

一道dp题 我还录制了视频讲解hh 一次操作时是2的k次方 然后每次可以对x或者y进程除2^K 下取整
那么怎么思考这个题呢 我们可以二进制进行拆 就60次的事情
我们把x y拆成二进制 他们肯定是有一个公共前缀的 那么这个前缀是要留的后面都是不要的
后面不同的数字是留不下来的 这个除2的k次方相当于左移k位
那么左移k位有几种方式呢 可以直接移k位 也可以分批次移动 比如5=2+3
他的操作代价明显比一次操作5更好的 所以可以看出其实移动就是一个01背包
题目也说了只能用一次一个k
然后说一下状态转移怎么来的
我们可以开三维来表示i x y 目前状态
最终答案就是x1=y1
然后每一次i移动 两个数都是能移的 所以
可以写dpixy=dpi-1 x-i y+代价
for (int i = 1; i <= 59; i++) {
for (int u = 0; u <= 59; u++) {
for (int v = 0; v <= 59; v++) {
dp[i & 1][u][v] = min(dp[i & 1][u][v], dp[(i & 1) ^ 1][u][v]);
if (u >= i) {
dp[i & 1][u][v] = min(dp[i & 1][u][v], dp[(i & 1) ^ 1][u - i][v] + (qpow(2, i)));
}
if (v >= i) {
dp[i & 1][u][v] = min(dp[i & 1][u][v], dp[(i & 1) ^ 1][u][v - i] + (qpow(2, i)));
}
}
}
}
for (int i = 0; i <= 59; i++) {
for (int j = 0; j <= 59; j++) {
if ((x >> i) == (y >> j)) {
ans = min(ans, dp[0][i][j]);
}
}
}
预处理下即可 这里是滚动数组写法 (i&1)^1 i=8那么结果就是9
https://codeforces.com/contest/2091/problem/F

是个dp 不过这个dp是一个前缀和的优化dp 先考虑转移吧
我们可以拆分成上下两行 与同一行之间的转移
上下两行的转移书写该怎么想呢 他转移距离范围是多少呢
题目给了一个d 如果同一行转移那么 i-d i+d 一定可以的
如果是上下 那么就y相差1 那么!! 我转移就要多考虑一个1带来的影响
那么这一行最多就只能到i+d-1了 d-1的平方+1肯定是不超过d平方的
然后我们先思考处理同行的转移吧
先初始化最后一行 X全为1 计算一个前缀和 然后我们再计算每一个点有多少个点可以来到他这一边
然后就知道每个点的同行转移pretot
pre[n][j] = ( ((pre[n][j - 1] + now[n][j])) % mod) % mod;
pretot[n][j]= (( pre[n][min(j + d, m)] - pre[n][max(j - d-1, 0 * 1LL)])+mod)%mod;
这个pretot只是求了单点的 并不能涵盖一个段内的所有总和
现在我们思考上下两行的转移
假设我在i行 那么i+1行可以转移过来的
很明显我需要快速知道我在j列 i+1有多少个点可以过来的 (这i个点也包含了同行转移到他自己的)
于是我们就需要求出一个一行的tot的前缀和 我们管他叫ans
ans[n][j] = ans[n][j - 1] + pretot[n][j];
预处理完毕
接下来
开始处理上下两行的转移
首先进行一次转移对于当前行的可行点 将上一行的所有可行答案先加上来
然后做一个前缀和 知道每个点的上下转移情况 然后再做一次前缀和 此时这个前缀和就是同行之间的转移了
最终就知道一个点包含上下同层的情况 再做一个ans的前缀和拿来存答案
for (int i = n - 1; i >= 1; i--) {
for (int j = 1; j <= m; j++) {
if (ma[i][j] == 'X') {
now[i][j] =( ans[i + 1][min(j + d-1, m)] - ans[i + 1][max(j - d+1-1, 0 * 1LL)]+mod)%mod;
// now[i][j] %= mod;
}
}
for (int j = 1; j <= m; j++) {
pre[i][j] = pre[i][j - 1] + now[i][j];
pre[i][j] %= mod;
}
for (int j = 1; j <= m; j++) {
if (ma[i][j] == 'X')
pretot[i][j] = (pre[i][min(j + d, m)] - pre[i][max(j - d-1, 0 * 1LL)]+mod) % mod;
}
for (int j = 1; j <= m; j++) {
ans[i][j] = (ans[i][j - 1] + pretot[i][j]) % mod;
}
}
https://codeforces.com/contest/1954/problem/D

dp 此题的trick 就是关于这种集合类型的 比如说
1 2 3 分 1 2 13 2 3 的这种算贡献的 可以排序
然后按照数量排序 那么子集的最后一个数绝对是数量最大的 那么 计算贡献可以围绕这个数来展开 称为绝对众数
这题题目其实是很绕的 来解释下题目意思吧
其实 就是说给你2^n个集合 比如 1 2 3 问你把集合内的颜色的都放进去要多少个袋子 每一个袋子只能装两个球 比如说 我现在
3
1 1 2
放1 3 要多少个袋子 答案是2 因为 1 3 然后再3单独放
此题又为什么是dp呢 因为他其实是一个01背包 因为可以放可以不放 才有2^n种集合嘛
然后我们知道贡献怎么算 比如说 你此时是j个球 你绝对众数如果大于他 那很明显需要ai个袋子 否则是多少呢 其实 ai+j/2 (上) 多出来的
然后我们定义fj是放j个球的方案 然后 每次计算就好了
const int mod = 998244353;
int f[range];
void solve(int t) {
cin >> n;
int m=0;
//真的是阅读理解题 读懂就已经很费事了
for (int i = 1; i <= n; i++) {
cin >> a[i];
m+=a[i];
}
sort(a+1,a+1+n);
int ans = 0;
f[0]=1;
for (int i = 1; i <= n; i++) {
for(int j=0;j<=m-a[i];j++)
{
ans=(ans+(j>a[i]?(j+a[i]+1)/2:a[i])*f[j]%mod)%mod;
}
for(int j=m;j>=a[i];j--)
{
f[j]=f[j]+f[j-a[i]]%mod;
}
}
cout<<ans<<endl;



 浙公网安备 33010602011771号
浙公网安备 33010602011771号