做题小结
呼 昨晚10号晚上装了一晚上终于弄好
今天下午本来搞oj 尝试了个把小时一下 感觉还是算了吧 现在没时间弄
然后学轮廓线dp 挺有意思的 真的很不错 难确实难
https://www.luogu.com.cn/problem/CF2021C2

这个题 别人说是个板子平衡树 不过不会的就换别的写法
关键做这个题要晓得 一个数字最小出现位置 后面重复出现其实都不用管的 因为第一个满足后面就可以随便插了
那么我们最做的时候就必须时刻知道这个数字的最小位置 并且需要动态更新 那么我可以开一个set数组
下标存1-n来表示每个数 然后set里面就是出现的所有位置
只要保证每个数都是有序 不插队就行
什么意思 就是i要比i-1晚出现就行或者i-1没有出现i也不行
这是简单判断不带删除操作的时候
如果要牵扯到删除
那么 我就必须要明白删的那个数字走了以后 会产生的影响是什么 以及新来的那个数字会产生什么影响?
删的影响 好处
可能我这个数字 i 他所在位置太前了导致了i-1比他后面 如果删了i 那么我们开始释放这个数字
坏处 可能我这一删除 你把我最前的删了后面次前来了比i+1还晚 那么我们会把i+1放进坏位置里
新来的影响 好处 我们不会把i+1给影响进坏位置 因为一个位置的更改只会影响最小的那个 所以细细一想就知道了
如果不影响最早位置 i+1不变 影响比之前更前了 还是不影响i+1
可能我这个数字 i 他现在所在位置比较前了然后原先i+1在他前面 那么我们释放i+1
坏处
太前了比i-1还前 给i整进坏位置了
整体代码比较难写 细节比较多
#include<bits/stdc++.h>
#define int long long
#define debug cout<<endl<<"----------"<<endl;
const int range = 2e5+10;
using namespace std;
int n, k;
int a[range];
//int s[range];
//int lowbit(int x) {
// return x & -x;
//}
//void change(int x, int k) {
// while (x <= n)s[x] += k, x = x + lowbit(x);
//}
//int query(int x) {
// int t = 0;
// while (x)t += s[x], x = x - lowbit(x);
// return t;
//}
int b[range];
set<int>s[range];
set<int>st;
int m, q;
void solve() { //多测
cin >> n >> m >> q;
map<int, int>ma;
st.clear();
ma.clear();
for (int i = 1; i <= n; i++) {
cin >> a[i];
ma[a[i]] = i;
s[i].clear();
}
for (int i = 1; i <= m; i++) {
cin >> b[i];
b[i] = ma[b[i]]; //映射到n的下标去
s[b[i]].insert(i);
}
for (int i = 2; i <= n; i++) {
if (s[i].size() && (!s[i - 1].size() || (*s[i - 1].begin() > *s[i].begin()))) {
st.insert(i);//3 4 2
}
}
//我控制不来 动态更新最小值 用set开二维是一个好办法
//导致一堆特判做的也不想写了
//前面那个人只看他的前面 不看后面 后面改变只会影响自己和后面
if (!st.size())
cout << "YA" << endl;
else cout << "TIDAK" << endl;
// for(int i=1;i<=n;i++)
// {
// cout<<i<<endl;
// for(auto j:s[i]){
// cout<<j<<" ";
// }
// cout<<endl;
// }
// cout<<"-----------"<<endl;
for (int i = 1; i <= q; i++) {
int x, y;
cin >> x >> y;
s[b[x]].erase(x);
if (b[x] < n && s[b[x] + 1].size() && ((*s[b[x] + 1].begin() < *s[b[x]].begin()) || !s[b[x]].size())) {
st.insert(b[x] + 1);
}
if ((s[b[x] - 1].size() && *s[b[x] - 1].begin() < *s[b[x]].begin()) || !s[b[x]].size()) {
st.erase(b[x]);
}
y = ma[y]; //得到初始位置
b[x] = y;
// cout<<"y:"<<y<<endl;
// s[b[x]].insert(y);
s[b[x]].insert(x);
//初始位置可能不变或者变得更前
//y的加入会带入新的问题 后面的 前面的
if (b[x] > 1 && ((s[b[x] - 1].size() && *s[b[x] - 1].begin() > *s[b[x]].begin()) || !s[b[x] - 1].size())) {
st.insert(b[x]);//
}//变的太前
// cout<<*s[b[x]-1].begin()<<" "<<*s[b[x]].begin()<<endl;
// cout<<endl;
// for(auto j:st){
// cout<<j<<" ";
// }
// cout<<endl;
//可能初始太后面了 我们变前了 让后面的得以变正确 不用特判后面空集
if ((b[x] < n && s[b[x] + 1].size() && *s[b[x] + 1].begin() > *s[b[x]].begin())) {
st.erase(b[x] + 1);
}
if (st.size()) {
cout << "TIDAK" << endl;
} else cout << "YA" << endl;
}
}
signed main() {
ios::sync_with_stdio();
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while (t--)
solve();
}
噢 我记起来了 我8 9号应该是装机去了 特别是9号晚上和wzz他们玩lol 结果晚上一个人玩了很多大乱斗都是输 直接卸载了 没意思
打个大乱斗要么你出收集者 要么他出 但是现在越来越不喜欢出这个了 k头没意思 但是现在是别人会出 你又没人头了 就玩不了
然后又一直输 输了一晚上 不想玩了 更别提排位和新的更新 不好玩 像手游
https://www.luogu.com.cn/problem/CF2022B

没做对
思路错了
#include<bits/stdc++.h>
#define int long long
#define debug cout<<endl<<"----------"<<endl;
const int range = 6e5+10;
using namespace std;
int n, k;
int a[range];
int s[range];
int lowbit(int x) {
return x & -x;
}
void change(int x, int k) {
while (x <= n)s[x] += k, x = x + lowbit(x);
}
int query(int x) {
int t = 0;
while (x)t += s[x], x = x - lowbit(x);
return t;
}
void solve(int t) { //多测
cin >> n >>k;
priority_queue<int>q;
for(int i=1;i<=n;i++)
{
cin>>a[i];
q.push(a[i]);
}
if(t==294)
{
cout<<n<<","<<k<<"|";
for(int i=1;i<=n;i++){
cout<<a[i]<<",";
}
cout<<endl;return ;
}
int ans=0;
while(q.size())
{
vector<int>v;
int w=q.size();
int x=min(w,k);
for(int i=1;i<=x;i++)
{
v.push_back(q.top());
q.pop();
}
int small=v[x-1];
ans+=small;
for(int i=1;i<=x;i++)
{
v[i-1]-=small;
if(v[i-1]){
q.push(v[i-1]);
}
}
}
cout<<ans<<endl;
}
signed main() {
ios::sync_with_stdio();
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
for(int i=1;i<=t;i++)
{
solve(i);
}
}
一个
3 2
2 2 2就错了 思考少了 我认为要4次 其实3次 因为我存在浪费
那么正解是
for(int i=1;i<=n;i++)cin>>a[i],sum+=a[i];
sort(a+1,a+1+n);
cout<<max(a[n],(sum+k-1)/k)<<endl;
有点逆天 逆天在我没想到。。。。。
https://www.luogu.com.cn/problem/U204941

这个题两种解法
一个状态压缩 一个轮廓线dp(一开始没看懂) 后者我还是学了蛮久的 今天晚上和hfh玩了会手游 主要是这个新手机想体验下 不然我肯定不会这么晚写题解了
下午学轮廓线我由于装oj浪费时间心态急了没学懂都快崩溃了
状压没什么好说的 直接枚举两个行 就行 董老师的视频说的也很全 上下&=0
0表示竖 插头是垂直方向
1表示横着的 插头向水平方向
那么我们考虑转移 对于可以放 明天再写吧 早上要去亲戚家吃饭的
1.12 12:00
判断某一点能否放置 看上面和右边即可
如果上面是1表示横放 那么不影响 如果是0 那么必然要竖放 否则上面是空着的 如果左边是0上面是1 那么 我们可以选择不放或者横放
还有就是预处理的问题
试想一下 我们在枚举上一行和这一行的状态的时候 肯定 存在 不合法的状态 试问如果出现二行状态合并好了 出现0没用 那肯定不行 两行
之间一定要用完 当然可以是上面是1这一次是0 但不能上面是0 因为一定要用完 所以 我们提前预处理 奇数0的二进制 如果两个行合并了 (|)
是奇数0的那种 肯定不行 奇数0一定会存在 一个0用不完 就是|的时候会有奇数0
for (int i = 0; i <= (1 << n) -1; i++) {
cnt = 0;
flag[i] = 0;
for (int j = 0; j < n; j++) {
if ((i >> j) & 1) {
if (cnt % 2) {
flag[i] = 1;
break;
}
cnt = 0;
} else cnt++;
}
if (cnt % 2)flag[i] = 1;
cout<<i<<" "<<flag[i]<<endl;
后续转移代码
试想为什么是F 0 0 = 1
很明显就能转移的都可以转移 因为k-k=0
f[0][0] = 1;
for (int i = 1; i <= m; i++) {
for (int j = 0; j <= (1 << n) -1; j++) {
//上一列
for (int k = 0; k <= (1 << n) -1; k++) {
if (!flag[j | k] && (j & k) == 0) {
f[i][j] += f[i - 1][k];
cout<<f[i][j]<<endl;
}
}
}
}
状压就这么写了 下面介绍轮廓线DP
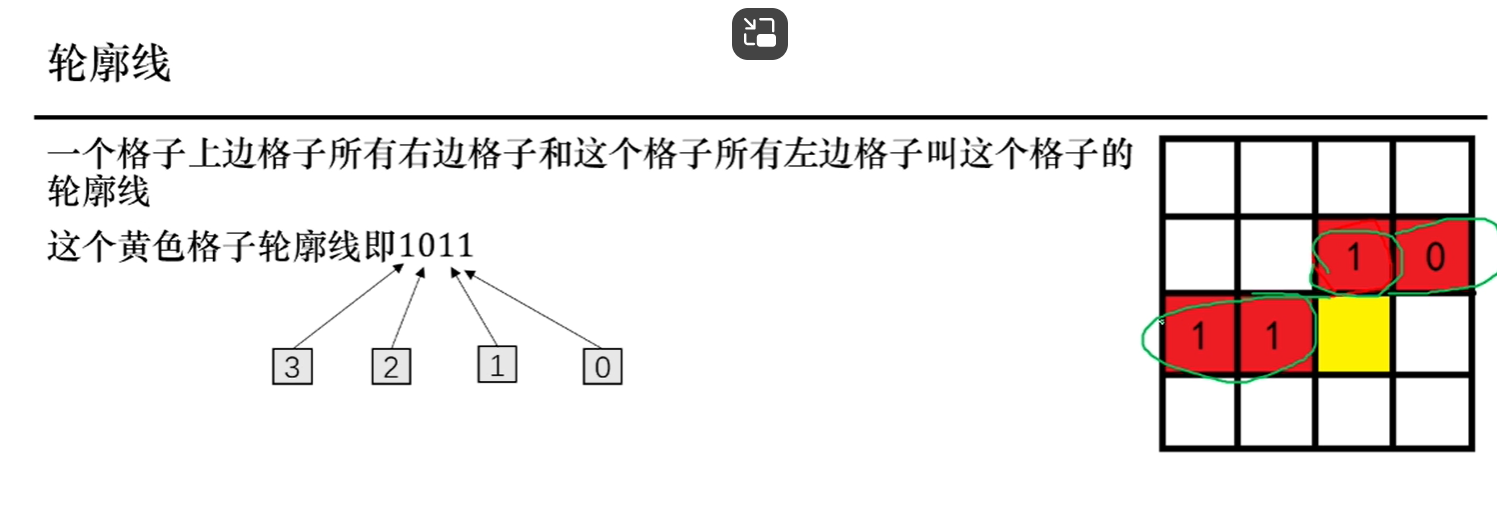
这个图很重要 二进制从右上->左边

下面是所有的情况 这个不再赘述
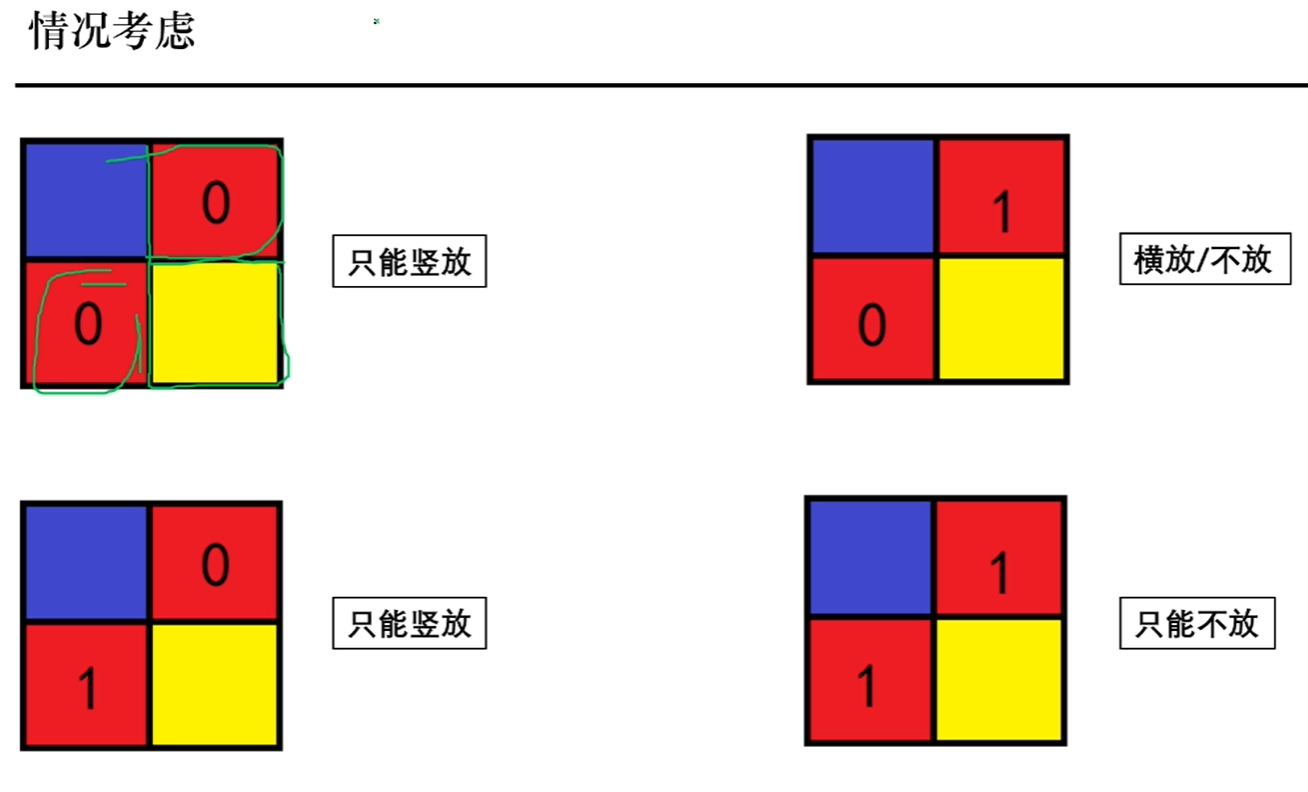
不放只需要左移1位多一个0即可 比如1011x 此时不放x为0 10110
竖放是左移加1 为什么呢 见下图 我们要把此时k5 pop掉 不管他是多少
因为都是要溢出的 我们毕竟要往右边推了 右边等会继承状态的是看x和k4
此时让k4为最高位才是真的
那么横放+3 很简单 两个1一放就行 xxx00 -> xxx11 等于+3


参考文章
https://www.cnblogs.com/caijiLYC/p/14358687.html
说下代码
f[0][(1<<m)-1]=1;//
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cur ^= 1;
memset(f[cur], 0, sizeof (f[cur]));
for (int k = 0; k < (1 << m); k++) {
if (k & (1 << (m - 1))) {
cal(k, k << 1);
}
if (i && !(k & (1 << (m - 1)))) {
cal(k, (k << 1) + 1);
}
if (j && (k & (1 << (m - 1))) && !(k & 1)) {
cal(k, (k << 1) + 3);
}
}
}
}
cout<<f[cur][(1<<m)-1]<<endl;
f[0][(1<<m)-1]=1;
if (k & (1 << (m - 1))) {
cal(k, k << 1);
}
这一步很巧妙
只有不放才能转移他 让后k<<1=2^M+1-2 再减去2^M就变成了
111111110如此表示 第一行第一个是0表示未放 符合我们的逻辑 后面就可以照常进行转移了
通过这一题大致理解了下轮廓线DP 感觉很有意思! 日后用的虽然少 但是不后悔花了时间去学
ps 今天早上肚子痛醒来 就睡了3个小时 然后中午下午在阿姨家吃饭 下午在睡觉 困死了 我当时趴着都能睡着 晚上回来补点题



 浙公网安备 33010602011771号
浙公网安备 33010602011771号