2024ICPC网络赛前总复习 2024.2.29复盘 30-40页
https://www.luogu.com.cn/problem/CF1934B

此题有完全背包写法 不再赘述
意识到我们不可能用3个1去换一个3 也不可能用2个3换一个6.。一次类推开几个for循环
void solve() {
int lte = 1e9;
cin >> n;
for (int i = 0; i <= 2; i++) {
for (int j = 0; j <= 1; j++) {
for (int h = 0; h <= 4; h++) {
for (int s = 0; s <= 2; s++) {
int now = i + j * 3 + h * 6 + s * 10;
int need = (n - now) % 15;
if (need != 0||n-now<0)continue;
else { //cout<<now<<endl;
int ans = i + j + h + s + (n - now) / 15;
lte = min(lte, ans);
}
}
}
}
}
cout<<lte<<endl;
}
https://www.luogu.com.cn/problem/CF1934C

考了一个曼哈顿距离 猜出其中一个地雷坐标
我们先查 1,1 查到了一条直线再查这两端点就行 这样就可以规避掉第二个点的影响了
也可以先查1 1 然后查n m 得到两条直线 后面查n 1 其中一个交点肯定是答案
很好的一道题
https://www.luogu.com.cn/problem/CF1873F

复习到了money trees 那就再讲清楚两种做法吧
第一种是二分长度做法 第二种是双指针做法
第一种二分长度 这种需要倒着for循环看最大延申长度 得到了最大长度然后使用前缀和
判断是否小于题目限制 后看是否满足二分的mid
bool check(int changdu)
{
for(int i=1;i<=n-changdu+1;i++)
{
if(sum[i+changdu-1]-sum[i-1]<=k)
{
if(c[i]-i+1>=changdu)return 1;
}
}
return 0;
}
第二种双指针 使用的最多的技巧
需要定义一个左指针l 然后不断延申出去 一旦大于题目限制就l++
int l=1;
int r;
for(int i=1;i<=n;i++)
{
if(h[i-1]%h[i]){
l=i;
}//题目另外的限制条件
while(sum[i]-sum[l-1]>k)
{
l++;
}
ans=max(ans,i-l+1);
}
https://www.luogu.com.cn/problem/CF1873H

tarjan抓捕问题 这个题讲了很多次了 深深印在我的脑子里 他很重要
我记得无向图tarjan我记得两个写法 一个是我的板子
还有就是说如果你碰到了更小的那个度数 此时那个点在stk里面 那就可以判断了
好像是这样 我有点忘记了 注意不是instk里
不过我这个板子的fa^1就已经够用了
然后注意多测情况 首先明白这是一个基环树 让我们复习一下他的性质
任意一个点有两条路径(就是完全是一个环) 并且和是n 有且只有一个环
对于环之外的树按照若干棵别的树做处理 再与环一起计算 这个后面会有题的 我没记错的话
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=400010;
int n;
int s,t;//s抓t
int low[maxn],dfn[maxn],tot;
int h[maxn],e[maxn],ne[maxn],idx;
int stk[maxn],scc[maxn],siz[maxn],top,cnt;
int vis[maxn];int instk[maxn];
int cntt[maxn][4];
int LTE[maxn];
vector<int>v[maxn];
void cclear()
{
top=0;cnt=0;idx=0;tot=0;
for(int i=0;i<=n;i++)h[i]=-1;
// cout<<h[2]<<endl;
for(int i=1;i<=n;i++)
{ v[i].clear();
LTE[i]=siz[i]=0;
instk[i]=ne[i]=e[i]=stk[i]=scc[i]=dfn[i]=low[i]=0;
cntt[i][1]=cntt[i][2]=0;
//wc wotm 服了 我在这里又初始h为0了 卧槽 卧槽 调一个小时
}
}
void add(int a,int b)
{ //cout<<a<<b<<" "<<h[a]<<"----------";
e[idx]=b;
ne[idx]=h[a];
// cout<<ne[idx]<<h[a]<<endl;
h[a]=idx++;
}//不能写正常的tarjan 因为这是无向图
//下面这个写法可以应对所有情况 但是instk不行
void tarjan(int x,int fa)
{
dfn[x]=low[x]=++tot;
stk[++top]=x;
// instk[x]=1;
for(int i=h[x];i!=-1;i=ne[i])
{
int j=e[i];
// cout<<"x: "<<x<<" J: "<<j<<endl;
if(!dfn[j]){
tarjan(j,i);
low[x]=min(low[x],low[j]);
}
else if(i!=(fa^1)){
low[x]=min(low[x],dfn[j]);
}
}
if(dfn[x]==low[x])
{
++cnt;
int y;
do{
y=stk[top--];
// instk[y]=0;
v[cnt].push_back(y);
// cout<<cnt<<" "<<y<<endl;
//不能不push因为 单个也会被tarjan视为一个强联通分量
scc[y]=cnt;
++siz[cnt];
}while(y!=x);
}
}
void bfs(int x)
{ queue<int>q;
int name;
for(int i=1;i<=n;i++)vis[i]=0;
if(x==s)name=1;
else name=2;
vis[x]=1;
q.push(x);
while(!q.empty())
{
int u=q.front();
// cout<<"母亲 "<<u<<endl;
q.pop();
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
if(!vis[j])
{
vis[j]=1;
cntt[j][name]=cntt[u][name]+1;
q.push(j);
}
}
}
}
void solve()
{
cin>>n;
cin>>s>>t;
cclear();
for(int i=1;i<=n;i++)
{
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
bfs(s);
bfs(t);
for(int i=1;i<=n;i++)
{
if(!dfn[i])tarjan(i,0);
}
for(int i=1;i<=cnt;i++)
{
if(siz[i]>=3)
{
for(auto hs:v[i])
{
LTE[hs]=1;
}
}
}
if(s==t){
cout<<"NO"<<endl;return ;
}
if(LTE[t]){
cout<<"YES"<<endl;return ;
}
for(int i=1;i<=n;i++)
{
if(LTE[i])
{
if(cntt[i][1]>cntt[i][2])
{
cout<<"YES"<<endl;
return;
}
}
}
cout<<"NO"<<endl;
return ;
}
signed main()
{
int tt;
cin>>tt;
while(tt--)solve();
return 0;
}
https://www.luogu.com.cn/problem/CF1850F

首先题目翻译有点傻逼
应该是每一秒对于的第i只青蛙跳ai 一眼就看出来了这是一个倍数有关的题目
很明显 暴力的话就是一个不是随机数的埃氏筛
这样会被全是1的毒瘤数据卡死了 导致n方 所以
我么只需要修改成整体埃氏筛即可
for(int i=1;i<=n;i++)
{
//if(ma[i]==0)continue;
for(int j=0;j<=n;j=j+i)
{
cnt[j]+=ma[i];
}
}
把j+=a[i]改成i就行了 这样就不会t 最终for扫一遍就行了
https://www.luogu.com.cn/problem/CF1850H

想了一会 没写出来 看了代码才发现是图论 当初自己写代码意识到了
。。。。写个递归就行了
非常好的一道题 如果某一时刻访问过却和以前冲突的 就是错的 直接输出
#include<bits/stdc++.h>
#define int long long
using namespace std;
struct node{
int v;
int w;
};
vector<node>e[200005];
int n;int m;
int a[200005];
int dis[200005];
map<int,int>mm;
bool flag=0;
void dfs(int ma,int q)
{
if(dis[ma])return ;//来到同一个点 如果是反向边没事 怕就怕重复
if(flag)return ;
//但是你q=0开始 dis就不会return 如果有那种重复情况
//但是特判这种情况 就很无语 因为你有反向边 一定会重复走到0
// 不过也有办法用那个from^1? 我不会
dis[ma]=q;
for(auto i:e[ma])
{
if(!dis[i.v])
//&&mm[dis[i.v]]<=1)
{
dfs(i.v,dis[ma]+i.w);
}
else {
if(dis[i.v]!=dis[ma]+i.w){
flag=1;
return ;
}
}
if(flag)return ;
}
}
void solve()
{
cin>>n;cin>>m;
mm.clear();
flag=0;
for(int i=1;i<=m;i++){
int a,b,c;
cin>>a>>b>>c;
e[a].push_back((node){b,c});
e[b].push_back((node){a,-c});
}
dis[1]=0;
for(int i=1;i<=n;i++)
{
if(!dis[i]){
dfs(i,1e15);
}
if(flag)break;
}
if(flag)cout<<"NO"<<endl;
else cout<<"YES"<<endl;
for(int i=1;i<=n;i++)
{
dis[i]=0;
e[i].clear();
}
return ;
}
https://www.luogu.com.cn/problem/CF1829F


雪花 说下我的口糊错误做法 我错在认为度数最高的一个点一定是根节点 这是错的
谁保证了那个纸条一定是3,4这样很小的 所以我们要抓住一个点
就是度数为1的那个叶子 知道了叶子的总数 然后也可以知道第二层的树 于是就做出来了
放我以前 直接秒了
void solve()
{
cin>>n;cin>>m;
set<int>s;
int ans=0;
for(int i=1;i<=m;i++)
{
cin>>a>>b;
v[a].push_back(b);
cnt[a]++;
v[b].push_back(a);
cnt[b]++;
}
for(int i=1;i<=n;i++)
{
if(cnt[i]==1)
{
ans++; s.insert(v[i][0]);
}
}
int x=ans/s.size();
cout<<s.size()<<" "<<x<<endl;
for(int i=1;i<=n;i++)
{
cnt[i]=0;
v[i].clear();
}
}
https://www.luogu.com.cn/problem/CF1829H

DP 好题
首先一定要观察数据范围 ai的取值仅仅到63 还有k也只是6而已
如果数据打了这题就没法做了
所以我们完全可以第二维暴力存数值就行了 然后等会把第二维单独
抽出来看满足k就行了
开一个二维dp
对于任何一个ai来说 我可以继承上一个 也可以不继承
不继承那就是从他这边重新开 然后这个也可以继承之前的数值
f[i][a[i]] = 1;
f[i][j] = (1ll * f[i][j] + f[i - 1][j]) % mod;
f[i][j & a[i]] = (1ll * f[i][j & a[i]] + f[i - 1][j]) % mod;
cin>>n;cin>>k;
int ans=0;
for(int i=1;i<=n;i++){cin>>a[i];}
for(int i=1;i<=n;i++)
{
dp[i][a[i]]=1;
for(int j=0;j<=63;j++)
{
dp[i][j]=(dp[i-1][j]+dp[i][j])%mod;
// dp[i][j&a[i]]=dp[i-1][j&a[i]]+dp[i][j&a[i]]%mod;
dp[i][j&a[i]]=(dp[i-1][j]+dp[i][j&a[i]])%mod;
}
}
for(int i=0;i<=63;i++)
{ int cnt=0;
for(int j=0;j<=6;j++)
{
if(i>>j&1){
cnt++;
}
}
if(cnt==k){
ans+=dp[n][i]%mod;
}
}
for(int i=1;i<=n;i++)
{
for(int j=0;j<=63;j++)
{
dp[i][j]=0;
}
}
cout<<ans%mod<<endl;
然后本题结束
https://www.luogu.com.cn/problem/CF1807E

一道可以拿来练手的交互二分 不难
https://www.luogu.com.cn/problem/CF1807F

很好的一道模拟题目 开dx dy模拟前进方向
if(s[0]=='D')dx=1;
else dx=-1;
if(s[1]=='L')dy=-1;
else dy=1;
x+=dx;
y+=dy
然后碰壁就是 x是否会是1 y是否会是m这样判断
cin>>n;
cin>>m;
cin>>x>>y;
cin>>tx>>ty;
string s;
int dx,dy;
cin>>s;
if(s[0]=='D')dx=1;
else dx=-1;
if(s[1]=='L')dy=-1;
else dy=1;
int lim=4*n*m;
int cnt=0;
while(lim--)
{
bool flag=0;
// cout<<x<<" "<<y<<" "<<dx<<" "<<dy<<endl;
if(x==tx&&y==ty){
cout<<cnt<<endl;
return ;
}
//shang
if(x==1&&dx==-1)
{
dx=1;//cnt++;
flag=1;
}//xia
if(x==n&&dx==1)
{ flag=1;
dx=-1;//cnt++;
}//zuo
if(y==1&&dy==-1)
{ flag=1;
dy=1;//cnt++;
}//you
if(y==m&&dy==1)
{ flag=1;
dy=-1;//cnt++;
}
if(flag)cnt++;
x+=dx;
y+=dy;
}
cout<<-1<<endl;
https://www.luogu.com.cn/problem/P1714

首先要明白我们是求一个m区间之内的连续和最大值 所以m就是一个窗口
然后求这个最大值 我么我们可以想到既然连续 前缀和很重要 于是可以单调队列一个前缀和最小值
那么我们就可以得到sumi-sum队头就是一个答案 然后不断刷新保存ans 最大就可以了
for(int i=1;i<=n;i++){
sum[i]=sum[i-1]+a[i];
}
// cout<<"ss"<<endl;
q[0]=0;
ans=sum[1];
sum[0]=0;
for(int i=1;i<=n;i++)
{
// cout<<sum[i]<<endl;
if(h<=t&&q[h]<i-k)h++;
ans=max(ans,sum[i]-sum[q[h]]);
//不是 sum[h]
while(h<=t&&sum[i]<=sum[q[t]])
{
t--;
}
q[++t]=i;
}
https://www.luogu.com.cn/problem/P1638

这题太典了 很明显一道单调队列
不过有点麻烦
队列保存的是一段队头不会重复的数字 队头一旦重复 就直接pop掉
那么对于此时如果达到了m 那么可以开始统计答案 a就是队头 那么 b就是 此时的i
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
const int range = 2e5 + 5;
int n;
int m;
int a[1000005];
int q[1000005];
set<int>s;
void solve() {
map<int, int>ma;
ma.clear();
int lte=1e9;
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
int h = 1;
int t = 0;
int x=1e9, b;
for (int i = 1; i <= n; i++) {
ma[a[i]]++;
//不能用if 否则就减一次 要找到只有一个的时候
while (h <= t && ma[a[q[h]]] > 1) {
ma[a[q[h]]]--;
h++ ;
}
q[++t] = i;
if (ma.size() == m) {
int ans=i-q[h];
if(ans<=lte)
{
if(h<x&&ans==lte)
{x = h;
lte=ans;
b = i;}
else if(ans<lte)
{
x = h;
lte=ans;
b = i;
}
}
}
}
cout<<x<<" "<<b;
}
signed main() {
ios::sync_with_stdio();
cin.tie(0);
cout.tie(0);
solve();
return 0;
}
https://www.luogu.com.cn/problem/CF1760G

这道题隔了好久再思考
思考了几分钟 少思考了一点东西 就是对b也要进行深搜 我一开始思考少了 你比如产生
断点的话 那a也搜不到b去
所以需要搜两次
然后答案很明显就是 某一时刻 a的map标记了 b搜的时候发现此时函数自身带的变量sum
ma[sum]有值的 那就有答案了
#include <bits/stdc++.h>
//hs lte
#define int long long
#define endl '\n'
using namespace std;
const int mod = 1e9 + 7;
int n;
int jc[200005];
struct node {
int v, w;
};
int a, b;
map<int, bool>ma;
bool flag = 0;
//队列清空
vector<node>e[100005];
int qpow(int a, int n) {
//a是模数 或者说的平方数
int ans = 1;
while (n) {
if (n & 1) ans = ans * a % mod;
a = a * a % mod;
n >>= 1;
}
return ans % mod;
}
int inv(int x) {
return qpow(x, mod - 2);
}
int C(int x, int m) {
// for (ll i = 1; i <= m; i++) {
// c[i] = c[i - 1] * (m - i + 1) % p * qpow(i, p - 2) % p;
// }
int g = (jc[x] * inv(jc[x - m]) % mod) * inv(jc[m]);
// cout<<endl<<"g "<<g<<endl;
return g % mod;
}
void adfs(int st, int fa, int sum) {
for (auto i : e[st]) {
if (i.v == fa || i.v == b)continue;
ma[sum ^ i.w] = 1;
adfs(i.v, st, sum ^ i.w);
}
return ;
}
void bdfs(int st, int fa, int sum) {
if (flag)return ;
for (auto i : e[st]) {
if (i.v == fa)continue;
if (ma[sum ^ i.w] == 1) {
flag = 1;
return ;
}
bdfs(i.v, st, sum ^ i.w);
//日了狗的 这里写了个adfs我草草草草
}
return ;
}
void solve(int t) {
int x, y, z;
cin >> n >> a >> b;
for(int i=1;i<=n;i++)
{
e[i].clear();
}
ma.clear();
flag=0;
for (int i = 1; i <= n - 1; i++) {
cin >> x >> y >> z;
e[x].push_back((node) {
y, z
});
e[y].push_back((node) {
x, z
});
}
ma[0]=1;
adfs(a, 0, 0);
bdfs(b, 0, 0);
//直接tp
if (flag) {
cout << "YES " << endl;
return ;
} else {
cout << "NO" << endl;
return ;
}
}
https://www.luogu.com.cn/problem/CF1722G

再回头只觉得简单 空出3个位置 统计好sum 别的就随便了
void solve()
{
cin>>n;
int sum=0;
for(int i=1;i<=n-3;i++)
{cout<<i<<" ";
sum^=i;
}
int a=1<<18;
int b=1<<19;
int x=sum^a^b;
cout<<a<<" "<<b<<" "<<x<<endl;
}
当时理解半天的题目呢
https://www.luogu.com.cn/problem/CF1703E

矩阵旋转问题 要学会公式怎么推就行了 别的就没什么了

只需要知道90度就行的 180不就90+90嘛
公式
https://www.luogu.com.cn/problem/P1130

一道橙dp 还挺有意思的 不过逻辑就那么多 没啥说的
就是题目不要理解错了 然后 注意+a[j][i]因为第i个步骤 适合新生练手
int n;int m;
int a[2005][2005];
int f[2560][2005];
void solve()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
cin>>a[i][j];
}
for(int i=1;i<=n;i++)
{
f[0][i-1]=f[m][i-1];
for(int j=1;j<=m;j++)
{
f[j][i]=min(f[j-1][i-1],f[j][i-1])+a[j][i];
}
}
// for(LL i=1;i<=n;i++){//循环n个步骤
// dp[0][i-1]=dp[m][i-1];//本题重点就在这里了!上一步的第零位,其实就是上一位的最后一位,因为最后一个小组是可以更换到1的
// for(LL j=1;j<=m;j++)//循环m个人,每一个步骤都有m个人可以完成,挨个儿决策
// dp[j][i]=min(dp[j-1][i-1],dp[j][i-1])+gay[j][i];//第i个人做第j步,可以由它的第j-1个步骤的第i-1个人或者第i个人转移过来
// }
int mini=1e8;
for(int i=1;i<=m;i++)
{
mini=min(mini,f[i][n]);
}
cout<<mini;
}
https://www.luogu.com.cn/problem/P8742

砝码称重 非常好一道题
可以两个加起来称某一个东西 也可以相减
那么代码书写 就是要前后扫一次dp 总共两次dp 我喜欢称这个为扫
然后 注意相减的那种要写成 dp[j]|=dp[j+a[i]]; 为什么呢
自己思考吧
int dp[range];
void solve()
{
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i],sum+=a[i];
dp[0]=1;
for(int i=1;i<=n;i++)
{
for(int j=sum;j>=a[i];j--)
{
dp[j]|=dp[j-a[i]];
}
}//xiangjiade
for(int i=1;i<=n;i++)
{
for(int j=1;j<=sum-a[i];j++)
{
//不能用两者相加造出来的砝码当作现有的
dp[j]|=dp[j+a[i]];
}
}
int ans=0;
for(int i=1;i<=sum;i++){
if(dp[i])ans++;
}
cout<<ans;
//
}
https://www.luogu.com.cn/problem/P1569

有点像刚才上面单调队列的前缀和问题 很像那个最大子序列
一般涉及到连续又要最大啥的 很难不dp
然后 这题 比如说 我们调了一个i就可以往前倒着找 看看最多构成几组 但是大于0的情况下
其实就是最大子序列 我都想删掉这个题了
void solve()
{
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
sum[i]=sum[i-1]+a[i];
if(sum[i]>=0)f[i]=1;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<i;j++)
{
if(f[j]>0&&sum[i]-sum[j]>=0)
{
f[i]=max(f[i],f[j]+1);
}
}
}
if(f[n]==0)cout<<"Impossible";
else cout<<f[n];
}
https://www.luogu.com.cn/problem/P1719
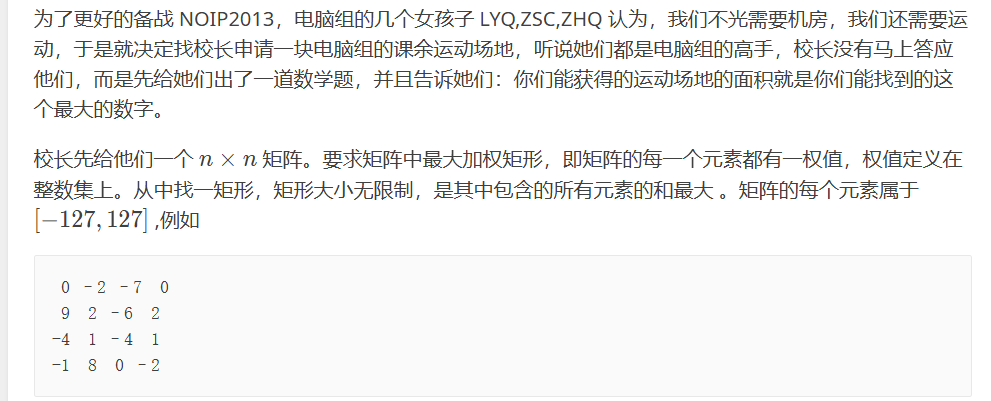
最大加权矩阵
非常好一道题 可以暴力用二位前缀和做 竟然不超时 我会讲复杂度分析
但是最关键还是要学会矩阵压缩
首先对于代码
void check() {
memset(dp, 0, sizeof dp);
for (int i = 1; i <= n; i++) {
dp[i] = max(dp[i - 1] + temp[i], dp[i]);
ans = max(ans, dp[i]);
}
}
void solve() {
for (int i = 1; i <= n; i++) {
memset(temp, 0, sizeof temp);
for (int j = i; j <= n; j++) {
for (int k = 1; k <= n; k++) {
temp[k] += a[j][k];
}
check();
}
}
}
对于solve函数 而言 注意到有三层循环
第一次 我们 会从第一行一直取到最后一行
第二次则是从第二行取到最后一行 每一次i变了 temp清空
然后temp是记载列的 不是行 注意
0 –2 –7 0
9 2 –6 2
-4 1 –4 1
-1 8 0 –2
比如 0+9 -2+2 这样的 列相加
然后我们 每次一个行的列统计完都会check一次 比如 一开始的
0 -2 -7 0
check函数里 dp[i] = max(dp[i - 1] + temp[i], dp[i]);
然后就是dpi-1如果说是小于0的 我们从第一列开始统计嘛 第一列小于0那dp1就是0
如果dp2+dp1反而小于0的 那第二列断开 默认dp2=0 dp1计入ans里去了
很灵活的
很好的模板
再来讲下On^4的做法 但是此题不会超时 数据小
for(int x1=1;x1<=n;x1++){
for(int y1=1;y1<=n;y1++){
for(int x2=1;x2<=n;x2++){
for(int y2=1;y2<=n;y2++){
if(x2<x1 || y2<y1) continue;//如果左上角比右下角还要大,就不用求了,下一个
mx=max(mx,sum[x2][y2]+sum[x1-1][y1-1]-sum[x2][y1-1]-sum[x1-1][y2]);//求最大值
}
}
}
}
分析这个复杂度才是我想说明的

等于这个
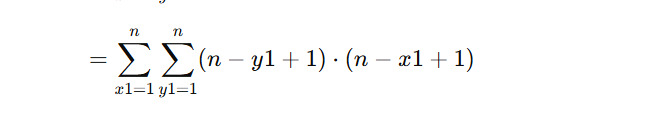
对于∑n-y1+1拆开就是


于是就是两个相乘 下面底数是4 肯定超不了的 这个复杂度计算很有意思
https://www.luogu.com.cn/problem/P1877

首先做dp一定要观察数据范围
优先考虑存数组表示 于是 转移就简单多了
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int range=2e5+5;
int n;
int beg;
int maxf;
int c[200005];
int dp[55][1005];
void solve()
{
//你可以看到我那个dp00=1
///不该这么写的 我老是忘记 dp[i][j]|=dp[i-1][j+c[i]]
//这个就是对是否取到j=0的情况呀 我老是忘
//老是以为这里j不是0 以为是c【i】
//
//切记
//切记 我老是这么认为
cin>>n;
cin>>beg>>maxf;
for(int i=1;i<=n;i++)cin>>c[i];
dp[0][beg]=1;
for(int i=1;i<=n;i++)
{
bool flag=0;
for(int j=0;j<=maxf;j++)
{
if(j>=c[i])
{
dp[i][j]|=dp[i-1][j-c[i]];//,flag=1;
}
if(j+c[i]<=maxf){
dp[i][j]|=dp[i-1][j+c[i]];//,flag=1;
}
//我这样思考还是周到 不是j+c小于就更新flag这不对
//我下面那个样例就说明了
if(dp[i][j])flag=1;
}
if(flag==0){
cout<<-1;
return ;
}
}
for(int i=maxf;i>=0;i--)
{
if(dp[n][i]){
cout<<i;
return ;
}
}
}
https://www.luogu.com.cn/problem/P9325

不可以考虑暴力做法
要体会到区间合并的概念
又大区间从小区间得到
观察以下 不难发现 5可以由3的来
4可以由2的来 于是此题做出来了

#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int range = 2e5 + 5;
int n;
int a[200005];
int h[range];
int b[range];
void solve() {
cin >> n;
for (int i = 1; i <= n; i++)cin >> h[i];
cout<<"0"<<" ";
for (int len = 2; len <= n; len++) {
int ans = 1e9;
if (len % 2 == 1) {
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
a[l] = a[l + 1] + abs(h[r] - h[l]);
ans = min(a[l], ans);
}
} else {
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
b[l] = b[l + 1] + abs(h[l] - h[r]);
ans = min(b[l], ans);
}
}
cout<<ans<<" ";
}
}
https://www.luogu.com.cn/problem/P2858

想了一下 就写出来了
观察好数据范围 发现完全可以用数组直接记录
于是考虑n n记录就行
然后 发现第t天 总共选了 多少个有两种可能
for(register int i=1;i<=n;i++)
for(register int j=0;j<=i;j++)
{
register int l=i-j;//推出右边取了多少个
dp[i][j]=max(dp[i-1][j]+in[n-l+1]*i,dp[i-1][j-1]+in[j]*i);//状态转移
//n-l+1就是从右边数第l个在in数组中的下标
}
翻到一个题解
dp[i][j]表示已经取了i个数,左边取了j个数的最优解
和我一样的思路 不过我以前做的话的思路是
for(int len=2;len<=n;len++)
{
for(int l=1;l+len-1<=n;l++)
{
int r=l+len-1;
dp[l][r]=max(dp[l+1][r]+v[l]*(n-len+1),dp[l][r-1]+v[r]*(n-len+1));
就是倒着思考了 反而是l或者r是最后才取到的意思 比如说2 - 7 我假设2是现在才取到 或者7现在才取到 我现在的思路反而不是这样的
不过没啥 没啥大区别 dp方程开对了就行
https://www.luogu.com.cn/problem/P3146

这个题不难想到区间dp 数据这么小
if(dp[l][k]==dp[k+1][r]&&>0)
对于l r 中间的值有大的尽量更新 我觉得是没后效性的 因为dp[l][r]
限定了只有l-r才有这个值 更别的也不冲突
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int range = 2e5 + 5;
int n;
int a[200005];
int dp[2004][2004];
void solve() {
cin >> n;
int ans = -1;
for (int i = 1; i <= n; i++)cin >> a[i],ans=max(a[i],ans);
for (int i = 1; i <= n; i++) dp[i][i] = a[i];
for (int len = 2; len <= n; len++) {
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
if (len == 2) {
for (int k = l; k < r; k++) {
if (dp[l][k] == dp[k + 1][r])
dp[l][r] = max(dp[l][r], dp[l][k] + 1);
ans = max(ans, dp[l][r]);
}
} else {
for (int k = l; k < r; k++) {
if (dp[l][k] == dp[k + 1][r]&&dp[l][k]!=0) {
dp[l][r] = max(dp[l][r], dp[l][k] + 1);
ans = max(ans, dp[l][r]);
}
}
}
}
}
cout<<ans<<endl;
}
https://www.luogu.com.cn/problem/P3205

首先这个题 给我的赶紧很熟悉
暑假好像做过类似的 不过不知道是不是区间dp
然后 这个题一定要搞清楚进来的顺序 以及大小
我自己打了一遍草稿才知道的
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int range=2e5+5;
const int mod=19650827;
int n;
int f[2005][2005][2];
int a[200005];
void solve()
{
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)f[i][i][0]=1;
for(int len=2;len<=n;len++)
{
for(int i=1;i+len-1<=n;i++)
{
int j=i+len-1;
if(a[i]<a[i+1])
{
f[i][j][0]+=f[i+1][j][0];
}
if(a[i]<a[j]){
f[i][j][0]+=f[i+1][j][1];
}
if(a[j]>a[j-1])
{
f[i][j][1]+=f[i][j-1][1];
}
if(a[j]>a[i]){
f[i][j][1]+=f[i][j-1][0];
//f[i][j-1][0] j在最右 i刚好弄进来 然后比不过 去了右边
}
f[i][j][0]%=mod;
f[i][j][1] %=mod;
}
}
//第i个人从左边来,他既然从左边来,
//要么第i+1人从左边来且h[i+1]>h[i];
//要么第j个人从右边来且h[j]>h[i];
//第j个人从右边来,他既然从右边来,
//要么第j-1人从右边来且h[j]>h[j-1];
//要么第i个人从左边来且h[j]>h[i];这样你i就该去右边
int hslte=(f[1][n][0]+f[1][n][1])%mod;
cout<<hslte;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号