做题小结 dp训练3
第一个

这道题 主要思考到一个不可以连续两步 以及最大往左移动5位 就像背包一样
所以我们开个二维的dp数组表示
for (int j = 1; j <=z ; j++) {
if (i + j *2<= k + 1 &&i-1>=1) {
dp[i][j] = max(dp[i][j - 1] + a[i - 1] + a[i], max(dp[i][j],dp[i-1][j]+a[i]));
}
}
注意到往左j步 产生回来的话就是j*2 然后这个就是一个边界条件判断
别的就没啥了 挺好的一道题目
int n;
int k;
int z;
int a[range];
int dp[range][30];
int sum[range];
void init()
{
for(int i=1;i<=n+5;i++){
for(int j=0;j<=z+5;j++)
{ a[i]=0;
dp[i][j]=0;
}
}
}
void solve() {
cin >> n >> k >> z;
for (int i = 1; i <= n; i++)cin >> a[i];
for(int i=1;i<=n;i++){
sum[i]=sum[i-1]+a[i];
}
// cout<<sum[35]<<endl;
// dp[1][0]=a[1];
for (int i = 1; i <= min(n, k + 1); i++) {
if (i <= k + 1) {
dp[i][0] = max(dp[i - 1][0] + a[i], dp[i][0]);
} else break;
// for(int j=1;j<=z;j++)
// {
// dp[i][j]=max(dp[i-1][j]+a[i],dp[i];
// }
//起始位置不算步数
for (int j = 1; j <=z ; j++) {
if (i + j *2<= k + 1 &&i-1>=1) {
// cout << i << " " << j << " " << i + j - 1 + 2 << endl;
dp[i][j] = max(dp[i][j - 1] + a[i - 1] + a[i], max(dp[i][j],dp[i-1][j]+a[i]));
}
//没有左移两次 有也没事
}
for(int j=1;j<=z;j++)
{
if(i+j*2<=k+1&&i+1<=n)
{
dp[i][j]=max(dp[i][j-1]+a[i+1]+a[i],max(dp[i][j],dp[i-1][j]+a[i]));
}
}
}
int ans = 0;
for (int i = 1; i <= min(n, k + 1); i++) {
for (int j = 0; j <= z; j++)
if (i + j == k + 1 && j == 0) {
ans = max(ans, dp[i][j]);
} else if (j > 0 && j * 2 + i == k + 1) {
ans = max(ans, dp[i][j]);
}
}init();
cout << ans << endl;
}
题目-字符串蓝题(现在是黄了)
这个题有点狗屎 要求挺多的 又要连着头尾 又要最后一样
不过我没想到最后一样这个其实不就是只输出dp[i][i]就行了
然后头尾其实就是二维表示下即可 dp[i][j]表示i开头j结尾的
然后就是一个状态转移方程
提取这个字符串的头尾
dp[i][j]=max(dp[i][j],dp[i][newt]+len)即可 这个j也是新的字符串的尾巴
然后注意dp[newt][neww]=len 记得赋值下就可以了
for(int i=1;i<=n;i++)
{
cin>>x;
int g=x[0]-'a'+1;
int gg=x[x.size()-1]-'a'+1;
int w=x.size();
for(int j=1;j<=26;j++)
{
if(dp[j][g])
dp[j][gg]=max(dp[j][gg],dp[j][g]+w);
}
dp[g][gg]=max(dp[g][gg],w);
}
for(int i=1;i<=26;i++)
{
ans=max(ans,dp[i][i]);
}
题

这个题 一开始题目读错了 后面才知道 翻转就行
我还以为是这样的操作 只能对位反转 给我思考了半天
然后其实就没什么了 四个情况 一一对应就好了 这边不列举了
int cost[range];
int a[range];
string s[range];
int dp[range][5];
string temp[range];
void solve() {
cin >> n;
for (int i = 1; i <= n; i++)cin >> cost[i];
for (int i = 1; i <= n; i++) {
cin >> s[i];
temp[i] = s[i];
reverse(temp[i].begin(), temp[i].end());
}
memset(dp, 0x3f, sizeof dp);
int ini = dp[0][0];
dp[1][0] = 0;
dp[1][1] = cost[1];
for (int i = 2; i <= n; i++) {
if (s[i] >= s[i - 1]) {
dp[i][0] = min(dp[i - 1][0], dp[i][0]);
} if (temp[i - 1] <= s[i]) {
dp[i][0] = min(dp[i - 1][1], dp[i][0]);
} if (temp[i] >= s[i - 1]) {
dp[i][1] = min(dp[i - 1][0] + cost[i], dp[i][1]);
} if (temp[i - 1] <= temp[i]) {
dp[i][1] = min(dp[i - 1][1] + cost[i], dp[i][1]);
}
}
int ans = min(dp[n][1], dp[n][0]);
if (ans == ini)cout << -1 << endl;
else
cout << min(dp[n][1], dp[n][0]) << endl;
}
树形

不错的一道好题
我写了个dfs。。。直接t飞了 我知道会t的。。。
后面思考正解 考虑dp二维表示可行不可行
反正最终答案一定是n对吧
我老是想说一件事情 就是写dp题要有一种大局观 就是上帝视角一样
有一种不拘泥小节的思想 看事情看的很远的视野
这个题就体现的很好
就像背包一样
我们开一层循环1-n 第二层表示 走到i的方式当然要取min k
其实就是个背包这个题。。。。
然后可行的就是j>=d的
状态转移
j>=d:
对于可行可以由可行与不可行转移过来
j<d
不可行呢 不可行不是说我不能从可行转移过来 那如果我之前选了d 此次我选的挺小的 就必须保存答案呀
for(int i=1;i<=n;i++)
{
for(int j=1;j<=min(k,i);j++)
{
if(j>=d)
{
dp[i][1]+=dp[i-j][0]+dp[i-j][1];
dp[i][1]%=mod;
}
else {
dp[i][1]+=dp[i-j][1];
dp[i][1]%=mod;
dp[i][0]+=dp[i-j][0];
dp[i][0]%=mod;
}
}
}
好题

for (int i = 1; i <= 1e3 + 10; i++) {
for (int j = 1; j <= i; j++) {
dp[i + i / j] = min(dp[i + i / j], dp[i] + 1);
}
}
你可以最多进行 k 次如下的操作:选择两个正整数i,x,使 ai 变成 ai+ai/x
这一步很帅 观察到n只有1000
考虑n方dp 当然你问我n大了怎么办
我也不会。。。这个dp也是很有技巧的 非常的帅
如果n大了其实你会发现到很多的j都是无用的 我想 优化的话应该要用到整除分块的思想 具体我就不知道怎么了 毕竟整除分块都是蓝模板了
跑最短路做不了的 边都建不了
然后dp写完之后 最主要还是要发现k是诈骗 实际上1e3的数据撑不了几十次 所以k多了就是浪费 所以我们太大的k直接输出就行
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 1e6 + 10;
int n;
int b[range];
int cost[range];
int dp[5000];
int k;
int ans[range];
void solve() {
//妈的 诈骗题 好坑啊 值得总结
memset(ans, 0, sizeof ans);
cin >> n >> k;
int tot = 0;
for (int i = 1; i <= n; i++)cin >> b[i];
for (int i = 1; i <= n; i++)cin >> cost[i], tot += cost[i];
//花费的价值
int sum = 0;
for (int i = 1; i <= n; i++) {
sum += dp[b[i]];
}
if (k >= sum) {
cout << tot << endl;
return ;
}
int maxn=0;
for (int i = 1; i <= n; i++) {
for (int j = k; j >= dp[b[i]]; j--) {
ans[j] = max(ans[j - dp[b[i]]] + cost[i], ans[j]);
maxn=max(maxn,ans[j]);
}
}
cout<<maxn<<endl;
// cout << ans[k] << endl;
}
signed main()
{
ios::sync_with_stdio();
cin.tie(0);
cout.tie(0);
memset(dp, 0x3f, sizeof dp);
dp[1] = 0;
for (int i = 1; i <= 1e3 + 10; i++) {
for (int j = 1; j <= i; j++) {
dp[i + i / j] = min(dp[i + i / j], dp[i] + 1);
}
}
int t;
cin >> t;
while (t--)
solve();
return 0;
}
状态压缩dp
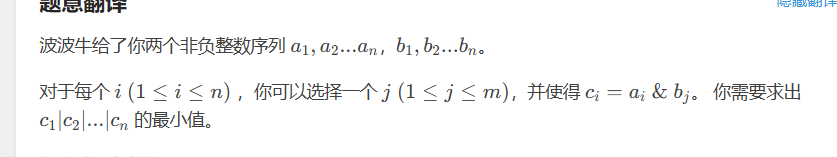
这个题 我思考错了 我也想了一个512*n的做法 不过 我后面就思考到了
还是那句话 没有全局观 其实dp数组交代不清楚
/ for (int i = 3; i <= n; i++) {
// int temp = now;
// bool flag = 0;
// for (int k = 0; k <= 520; k++) {
// if ( dp[i][k] && !flag) {
// now = k | temp;
// flag = 1;
// }
// else if (dp[i][k] && flag)
// now = min(now, k | temp);
// }
这里的dp数组是那个到i可以成多少的意思 然后就可以了
这种dp开法也是很常见的 说实话
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
int w=a[i]&b[j];
for(int k=0;k<=512;k++)
dp[i][k|w]|=dp[i-1][k];
}
}
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range=1000+10;
int n;int m;
int b[range];
int a[range];
int dp[300][range];
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=m;i++)cin>>b[i];
dp[0][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
int w=a[i]&b[j];
for(int k=0;k<=512;k++)
dp[i][k|w]|=dp[i-1][k];
}
}
for(int i=0;i<=512;i++)
{
if(dp[n][i]){
cout<<i<<endl;return ;
}
}
}
signed main()
{
ios::sync_with_stdio();
cin.tie(0);
cout.tie(0);
solve();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号