做题小结 DP训练1
第一个

开了个二维数组表示删除不删除
然后去重了下 如果前后相差为1的话 ,就可以进行删除的思考 此时i要删除
的话 i-1必须要不删除 如果i不删除的话 存一个前面的max即可
这边注意下可能有重复的数
如果前后相差不为1的话 我们就可以肆无忌惮 怎么搞都行
此题结束
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 3e5 + 10;
int n;
int a[range];
map<int,int>ma;
int dp[range][3];
int b[range];
int cnt=0;
void solve() {
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
if(ma[a[i]]){ma[a[i]]++;continue;}
else b[++cnt]=a[i],ma[a[i]]++;
}
sort(b + 1, b +1 + cnt, greater<int>());
for (int i = 1; i <= cnt; i++) {
if (b[i - 1] - b[i] == 1) {
dp[i][0]=max(dp[i][0],max(dp[i-1][1],dp[i-1][0]));
dp[i][1]=max(dp[i][1]+(b[i]*ma[b[i]]),dp[i-1][0]+(b[i]*ma[b[i]]));
} else {
dp[i][0]=max(dp[i-1][1],dp[i-1][0]);
dp[i][1]=max(dp[i-1][1],dp[i-1][0])+(b[i]*ma[b[i]]);
}
}
cout<<max(dp[cnt][1],dp[cnt][0])<<endl;
}
第二题
这题和上一题相对比起来更难了

int dp[range][4][10];
dp[1][0][0] = 0; 不动
dp[1][1][1] = 1; //左
dp[1][1][2] = 0; //右边
我这边默认左可删的 如果在距离够的情况下 但是右边可以不可以删除取决于后面的距离够不够
dp[i][0][0] = max(max(dp[i - 1][0][0], dp[i][0][0]), max(dp[i - 1][1][1], dp[i - 1][1][2]));
if (x[i] - x[i - 1] > h[i] && x[i] - x[i - 1] <= h[i] + h[i - 1]) {
dp[i][1][1] = max(max(dp[i - 1][0][0] + 1, dp[i][1][1]), max(dp[i - 1][1][2], dp[i - 1][1][1] + 1));
} else if (x[i] - x[i - 1] > h[i] + h[i - 1]) {
dp[i][1][1] = max(max(dp[i - 1][0][0] + 1, dp[i][1][1]), max(dp[i - 1][1][2] + 1, dp[i - 1][1][1] + 1));
}
if (x[i + 1] - x[i] > h[i]) {
dp[i][1][2] = max(max(dp[i][1][2], dp[i - 1][0][0] + 1), max(dp[i - 1][1][2] + 1, dp[i - 1][1][1] + 1));
}
完整代码 逻辑很清晰
第三
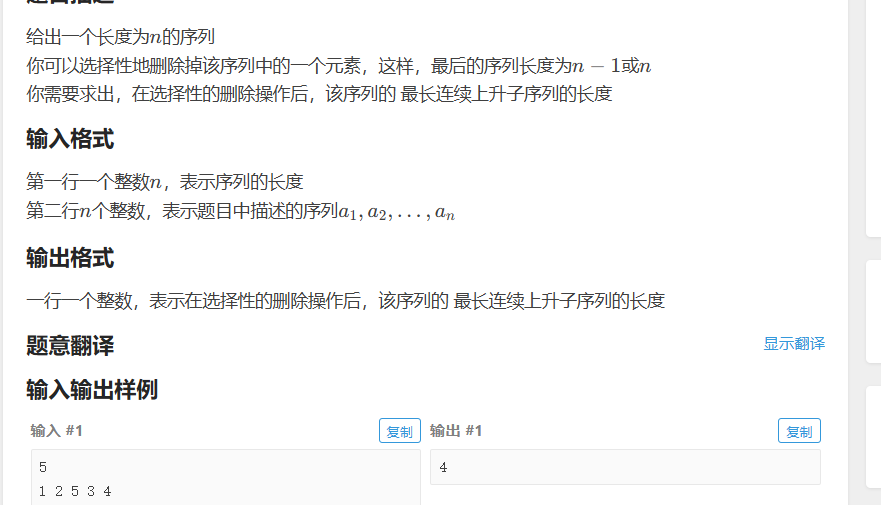
这题没做出来
我们要思考到 我们只有一次的操作机会
所以我们只能对那种中间夹了个没用的数进行删除
本来是上升的 由于这个数改变了
思考到这个就简单了 我们求一个后缀 二者拼在一块就是答案
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 3e5 + 10;
int n;
int a[range];
int dp[range];
int houzhui[range];
void solve() {
cin >> n;
int ans = 0;
for (int i = 1; i <= n; i++)cin >> a[i];
dp[1] = 1;
ans=1;
for (int i = 2; i <= n; i++) {
if (a[i - 1] < a[i]) {
dp[i] = dp[i - 1] + 1;
ans = max(ans, dp[i]);
} else dp[i] = 1;
}
houzhui[n]=1;
for (int i = n; i >= 1; i--) {
if (a[i] < a[i + 1]) {
houzhui[i] = houzhui[i + 1] + 1;
} else houzhui[i] = 1;
}
for (int i = 1; i <= n; i++) {
if ((a[i + 1] - a[i]) * (a[i + 2] - a[i + 1]) <= 0 && a[i] < a[i + 2] && i + 2 <= n) {
// debug
// cout << i << endl;
// cout << dp[i] << " " << houzhui[i + 2] << endl;
ans = max(ans, dp[i] + houzhui[i + 2]);
}
}
cout << ans << endl;
}
第四个题
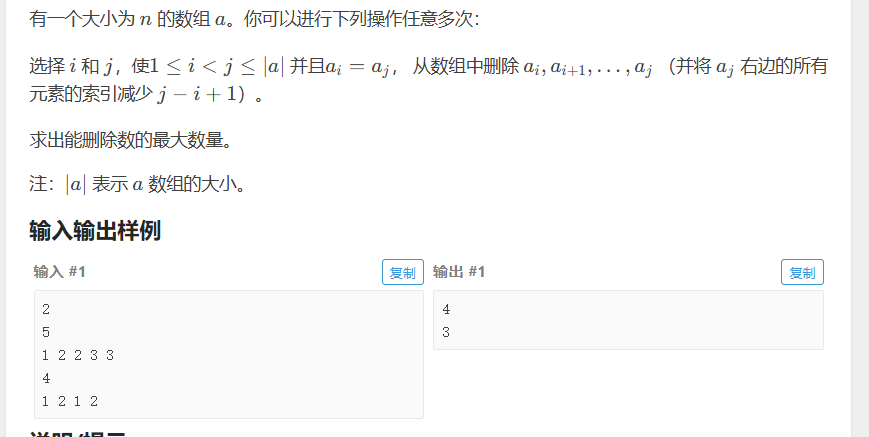
非常好的一个题
没做出来 这题蛮有意思的 真没想到
因为我没想到这个状态转移方程
fi=max(fi-1,fj-1+i-j+1)
如果暴力做 是个n方的写法
考虑优化 可以发现fj-1-j+1可以弄成一个东西
于是使用map代替下

for(int i=0;i<=n;i++)
{ dp[i]=0;cnt[i]=-1e9;}
//这题我不会
//dp[i]=dp[i-1],dp[j-1]+i-j+1
//做dp要先从n^2的情况下推转移方程 然后去优化
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)
{
dp[i]=max(dp[i-1],i+cnt[a[i]]+1);
cnt[a[i]]=max(cnt[a[i]],dp[i-1]-i);
}
cout<<dp[n]<<endl;
下一个概率dp

4 3
4 3 2 1
1 0.3
3 1
4 0.6
0.600000
很有意思的一道概率dp
我就讲正解思路了
给出这么多组操作 真正有用的其实就是第一个我们要一次到位的那个数
举个例子 4 2 1 3 5 就是那个4 能直接操作4的那个才有用
于是我们可以知道这个转移方程式就是ans=ans+(1-ans)*p
初始ans=0 我们假设第一次操作成功=p 后面就是说第一次不成功。。第二次也不成功。。。。。
很好一个题

题

这个题我的思路就是对于a分类
有两种a一个是做第一个位置的a 另一个是最后位置的
然后求一个后缀和对于第二类的a然后再for循环碰到a的话
dp[i][1] = dp[i - 1][1] + 1;
dp[i][2] = dp[i - 1][2];
dp[i][3] = max(dp[i-1][2] + asum[i],dp[i][3]);
这是b
dp[i][1] = dp[i - 1][1];
dp[i][2]=max(dp[i-1][1],dp[i-1][2])+1;
dp[i][3]=max(dp[i][2]+asum[i],dp[i][3]);
就这样了 就ac了 想的话 还好
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 3e5 + 10;
int n;
int a[range];
int dp[range][3];
string s;
int asum[range];
int bsum[range];
void solve() {
cin >> s;
n = s.size();
int ans=0;
s = ' ' + s;
for (int i = n; i >= 1; i--) {
if (s[i] == 'a')asum[i] = asum[i + 1] + 1;
else asum[i] = asum[i +1];
}
for (int i = 1; i <= n; i++) {
if (s[i] == 'a') {
dp[i][1] = dp[i - 1][1] + 1;
dp[i][2] = dp[i - 1][2];
dp[i][3] = max(dp[i-1][2] + asum[i],dp[i][3]);
} else {
dp[i][1] = dp[i - 1][1];
dp[i][2]=max(dp[i-1][1],dp[i-1][2])+1;
dp[i][3]=max(dp[i][2]+asum[i],dp[i][3]);
}
ans=max(dp[i][3],ans);
}
cout<<ans<<endl;
}
题

这是一个橙题 不过我觉得挺有意思的 很体现dp思想
对于一个正方形 我们就必须想到 一个点作为正方形的右下
那就必须满足他的左边 上面 对角 都要有值 而且这个值大家都要用 否则
无法构成正方形的 于是 状态转移就出来了 取一个min就可以了
int dp[105][105];
void solve()
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(a[i][j]==1)
{
dp[i][j]=min(dp[i-1][j],min(dp[i][j-1],dp[i-1][j-1]))+1;
ans=max(ans,dp[i][j]);
}
}
}
cout<<ans<<endl;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号