做题小结
接上一篇博客
第一题
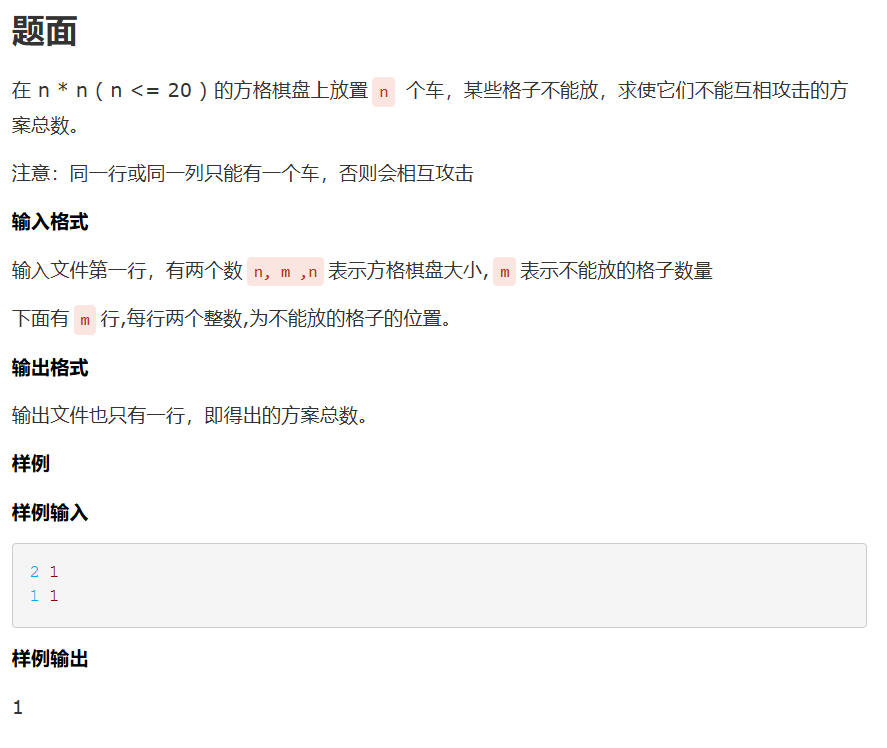
对于一列来说 只能放一个 一行也是同理 形成一个十字
又因为某些格子不能放 于是我们可以让不能放的格子如同炮兵阵地一样
不能放的位置为0
然后其实可以发现 每一行和上一行有关 可以让上一行承接之前所有
行的状态 类似一个前缀和
懒得写滚动了 反正n小
于是我们可以写出一个表达式
dp[i][j]表示第行的第j个列
对于转移方程式
如果j没有
则有dp[i][j]=max(dp[i-1][j]+1,dp[i][j]);这是错的理解!
j不能是列 j是列的话 转移状态很麻烦 某一列j是没有放的
可以放 那么这次放上了 其实我们也可以选择不放 那还要开个维[2]
表示放没放 那太麻烦了 转移起来 这也是状态压缩的出现意义
但是!!!j到底是什么呢 j是列是错的 因为是承接前面的 这个i-1行会有很多“1” 分别对应了i-1 i-2 的状态 所以这里其实就是1<<n-1种状态了 对于某一个i 1的个数不能大于i 对吧
所以这个二维你可以理解为1<<n的某种状态 而不是列
然后呢 我之前说了是承接上面的行
比如 10010101
可以由10000101的来 也可以是00010101的来所以是个+
所以这个dp转移就出来了
我们想想该如何开展循环
for(1-20)for(0-1<<20)应该是这样的 如果1的个数大于i直接continue
然后用lowbit函数进行转移
看了下代码 发现第一层循环其实不用。。加上的话我算了下
20 * 5e5 * 15 估摸可能要超时。。。。这个是往多了算。。。
好吧 直接上代码
for(int j=i;j>=1;j-=lowbit(j))
{
if((a[cnt]|lowbit(j))>a[cnt])
{
// debug
// cout<<i<<" "<<j<<" "<<lowbit(j)<<endl;
//a[cnt]&j==0
int temp=i^(lowbit(j));
dp[i]+=dp[temp];
// cout<<dp[i]<<" "<<i<<" "<<temp<<endl;
//我直接 dp[cnt]+=dp[lowbit(j)了 错了
}
}
下一个

是个区间dp 括号匹配
然后记住 像这种转移的方程是很正常的
一头一尾
dp[l][r]=dp[l+1][r],dp[l][r-1];
#include <iostream>
#include<map>
#include<algorithm>
#include<cstring>
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int range = 3e5 + 10;
int n;
int a[range];
string s;
int dp[1000][1000];
void solve() {
while (cin >> s) {
for(int i=0;i<=s.size()+10;i++)
{
for(int j=0;j<=s.size()+10;j++)
dp[i][j]=0;
}
if (s == "end")return ;
n = s.size() ;
map<char, int>ma;
map<char, int>num;
num['('] = 1;
num['['] = 1;
num[')'] = 0;
num[']'] = 0;
ma['('] = 1;
ma[')'] = 1;
ma['['] = 2;
ma[']'] = 2;
s = ' ' + s;
int ans = 0;
for (int len = 2; len <= n; len++) {
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
for (int k = l + 1; k < r; k++) {
if (ma[s[l]] == ma[s[k]] && s[l] != s[k] && num[s[l]] == 1)
dp[l][r] = max(dp[l+1][k-1] + dp[k + 1][r] + 1, dp[l][r]);
}
if (ma[s[l]] == ma[s[r]] && s[l] != s[r] && num[s[l]] == 1)
dp[l][r] = max(dp[l+1][r-1] + 1, dp[l][r]);
dp[l][r] = max(dp[l + 1][r], max(dp[l][r - 1], dp[l][r]));
ans = max(dp[l][r], ans);
// debug
// cout << len << endl;
// cout << ans << " " << dp[l][r] << " " << l << " " << r << endl;
}
}
cout << ans * 2 << endl;
}
}
下一个
和能量项链很像这一道题 肯定是要断环为链的
然后注意二层循环肯定是要更新到l+len-1<=2n
为什么呢 比如n+1想和n+3连一块儿 也是可以的呀 所以也要更新的
然后一层循环和项链不同的是 我们只需要到n即可 而那个题是因为要计算尾巴 答案区间长度是n+1 我一开始写的是n+1
别的就没什么了 一开始固定长度为3 就行了
ICPC2023网络赛

这个题是2023网络赛的 状态压缩的dp
可以分析到dp需要存到7个状态 分别表示小写 大写 大小写
小数字 大数字 大小数字 啥都没有
其实就是000 001 011 ----111这样
那么我们该思考如何书写转移方程式呢
dp数组很明显就是dp[i][x][7]了 表示此时i个以x结尾
因为不能相邻所以弄个结尾
转移方程该如何书写呢
假设我么当前字符是小写字母 是不是之前无小写的都可以通过转移对吧
然后对于之前含有小写的意味着我们也可以把答案转移过来
我们可以认为|1就是把1带上了 |2就是把大写带上了 |4就是数字带上了
我在写这一篇题解都在口胡上次的做法 能说多少算多少
假设此时是小写 直接外面枚举一层for循环从0到7
里层是for从小写a到数字结束中间有个小写会排斥要continue
然后dp[i][x][j|1]+=dp[i-1][k][j]
然后题目说了可以当大写 没关系同样的写法再来一遍
dp[i][x][j|2]+=dp[i-1][k][j]
此时x是大写了
对于大写的话 dp[i][x][j|1]+=dp[i-1][k][j]就这样
是数字的话 dp[i][x][j|4]+=dp[i-1][k][j]就这样
如果是“?”
他可以充当任何对吧
for(int i=0-7)
for(j=0;j-62)直接枚举每一位的可能性
比如这一位是数字 那么就当数字处理了 那么此时这个的答案转移
也是开一层循环进行叠加
是小写字母 由于可以当大写 于是可以 写两个转移 如果是大写再写一个
这样程序就写完了 然后输出答案的话就是dp[n][k][7]哪个大用哪个
应该是这样的吧
卧槽 什么 前缀和 淦
用前缀和 是个好办法 我那个估摸着不会超时吧?
我算算n762*62 我多算了一层循环
我这里指的是?字符时 要计算x目前是什么 然后还要知道上一个
选的什么
因为那个累计答案 我还要考虑上一个具体选了什么 就是那个k。。。
要超时了 用前缀和确实可以诶
前缀和数组记录上一层的7个状态
然后一减去当前的同样的的就肯定是上一层的所有答案了 我去
不错不错不错。。。。 重新思考果然更有体会了
要开滚动 这没话说
总体思路没问题 就是没想起要开前缀和优化 然后对于每个状态我都提到了要开for(0-7)其实开外面 大家一起用就行了 代码更简洁
很好的一道状态压缩题!
至此 应该是所有题目整理完了 当然那些场切的 我觉得没啥的 就没写了
#include <bits/stdc++.h>
#define endl '\n'
#define debug cout<<endl<<"----------"<<endl;
using namespace std;
const int mod = 998244353;
const int range = 1e5 + 10;
int n;
int dp[10][70][10];
char s[range];
long long sum[10];
void solve() {
scanf("%d",&n);
scanf("%s",s+1);
dp[0][63][0] = 1;
//1 小写 2大写 3大小写 4 数字 5数字+小写 6 数字+大写 7什么都有
//j表示选的东西 此时
for (int i = 0; i <= n - 1; i++) {
for (int j = 1; j <= 63; j++)
for (int k = 0; k <= 7; k++)
dp[(i + 1) & 1][j][k] = 0;
//必须清空 不然会重叠
for (int j = 0; j <= 7; j++)
sum[j] = 0;
for (int k = 0; k <= 7; k++)
for (int j = 1; j <= 63; j++)
sum[k] += dp[i & 1][j][k], sum[k] %= mod;
for (int k = 0; k <= 7; k++) {
if (s[i + 1] == '?') {
for (int j = 1; j <= 26; j++) {
dp[(i + 1) & 1][j][k | 1] =( ((sum[k] - dp[i & 1][j][k]) % mod) + dp[(i + 1) & 1][j][k | 1]+mod)%mod;
dp[(i + 1) & 1][j][k | 1] %= mod;
//k=5 25 + 9=34
}
for (int j = 27; j <= 52; j++) {
dp[(i + 1) & 1][j][k | 2] =( ((sum[k] - dp[i & 1][j][k]) % mod) + dp[(i + 1) & 1][j][k | 2]+mod)%mod;
dp[(i + 1) & 1][j][k | 2] %= mod;
}
for (int j = 53; j <= 62; j++) {
dp[(i + 1) & 1][j][k | 4] =( ((sum[k] - dp[i & 1][j][k]) % mod) + dp[(i + 1) & 1][j][k | 4]+mod)%mod;
dp[(i + 1) & 1][j][k | 4] %= mod;
}
} else {
if (s[i + 1] >= 'a' && s[i + 1] <= 'z') {
int x = s[i + 1] - 'a' + 1;
dp[(i + 1) & 1][x][k | 1] =( ((sum[k] - dp[i & 1][x][k]) % mod) + dp[(i + 1) & 1][x][k | 1]+mod)%mod;
dp[(i + 1) & 1][x][k | 1] %= mod;
x = x + 26;
dp[(i + 1) & 1][x][k | 2] = (((sum[k] - dp[i & 1][x][k]) % mod) + dp[(i + 1) & 1][x][k | 2]+mod)%mod;
dp[(i + 1) & 1][x][k | 2] %= mod;
} else if (s[i + 1] >= 'A' && s[i + 1] <= 'Z') {
int x = s[i + 1] + 32 - 'a' + 1 + 26;
dp[(i + 1) & 1][x][k | 2] = (((sum[k] - dp[i & 1][x][k]) % mod) + dp[(i + 1) & 1][x][k | 2] +mod)% mod;
dp[(i + 1) & 1][x][k | 2] %= mod;
} else if (s[i + 1] >= '0' && s[i + 1] <= '9') {
int x = 53 + s[i + 1] - '0';
dp[(i + 1) & 1][x][k | 4] = ((((sum[k] - dp[i & 1][x][k]) + mod) % mod + dp[(i + 1) & 1][x][k | 4]+mod)) % mod;
dp[(i + 1) & 1][x][k | 4] %= mod;
}
}
}
}
int ans = 0;
for (int j = 1; j <= 62; j++) {
ans += dp[n & 1][j][7];
ans %= mod;
}
cout << ans << endl;
}
int main() {
solve();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号