树链剖分
树链剖分
先来回顾两个问题:
1.将树从x到y结点最短路径上所有节点的值都加上z
这也是个模板题了吧
我们很容易想到,树上差分可以以O(n+m)的优秀复杂度解决这个问题
2.求树从x到y结点最短路径上所有节点的值之和
lca大水题,我们又很容易地想到,dfs O(n)预处理每个节点的dis(即到根节点的最短路径长度)
然后对于每个询问,求出x,y两点的lca,利用lca的性质
\(distance ( x , y ) = dis ( x ) + dis ( y ) - 2 * dis ( lca )\)
求出结果
时间复杂度 \(O(mlogn+n)\)
现在来思考一个\(bug\):
如果刚才的两个问题结合起来,成为一道题的两种操作呢?
刚才的方法显然就不够优秀了(每次询问之前要跑dfs更新dis)
树链剖分华丽登场
树剖是通过轻重边剖分将树分割成多条链,然后利用数据结构来维护这些链(本质上是一种优化暴力)
原理
树链剖分是根据轻重儿子,将一棵树剖成多条链,然后就可以用数据结构来维护这些链了,听着似乎还是有点像暴力,不过因为一条链有多个结点,所以可以优化时间复杂度。
首先明确概念:
重儿子:父亲节点的所有儿子中子树结点数目最多(size最大)的结点;
轻儿子:父亲节点中除了重儿子以外的儿子;
重边:父亲结点和重儿子连成的边;
轻边:父亲节点和轻儿子连成的边;
重链:由多条重边连接而成的路径;
轻链:由多条轻边连接而成的路径;
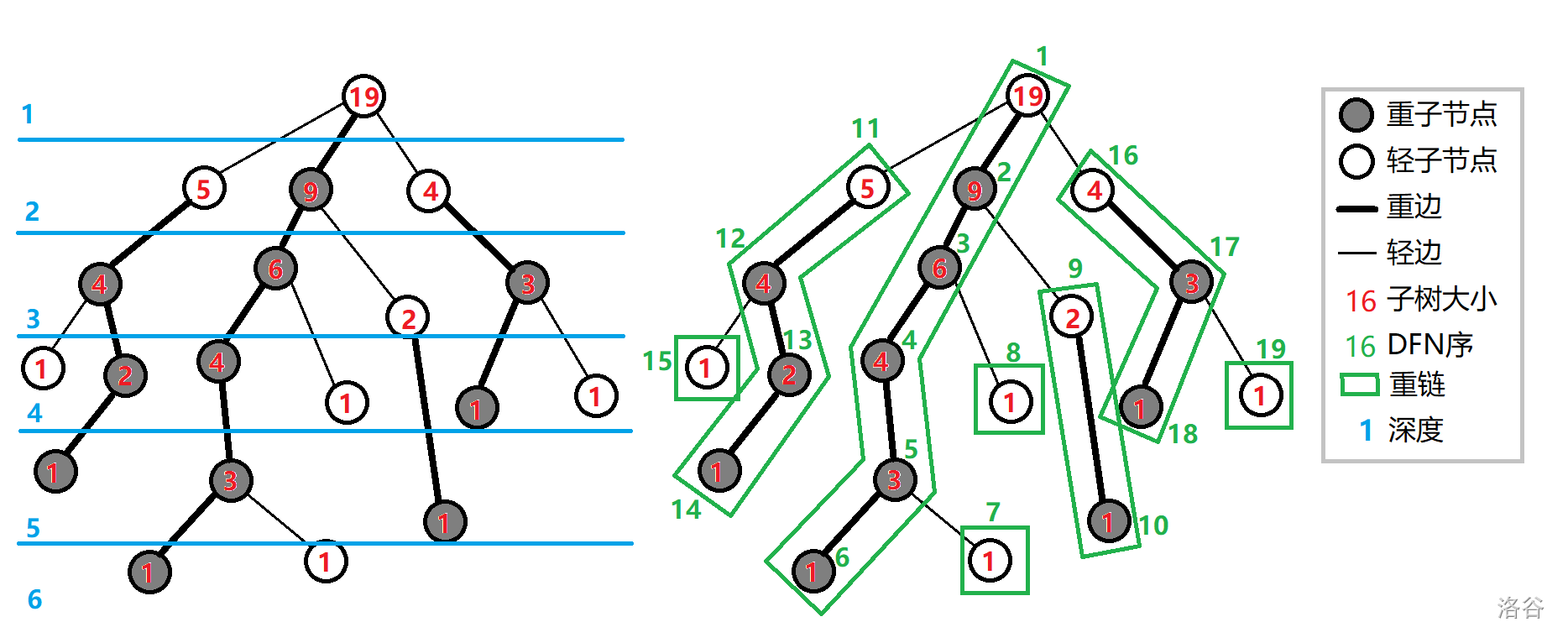
比如右边的图,黑点下就是当前重链的点,用绿框框住的就是每个点的重边
变量意义:
\(son[N]\) 重儿子
$f[N] $ 父亲
\(pre[N]\) 前驱
$dep[N] $ 深度
$Size[N] $ 本条链的大小
\(w[N]\) 每个点的价值
\(dfn[N]\) dfs序
$top[N] $ 每条链的顶端点
代码解释:
感觉不是很难,主要是理解了就明白了,就不放解释了
维护链
dfs序
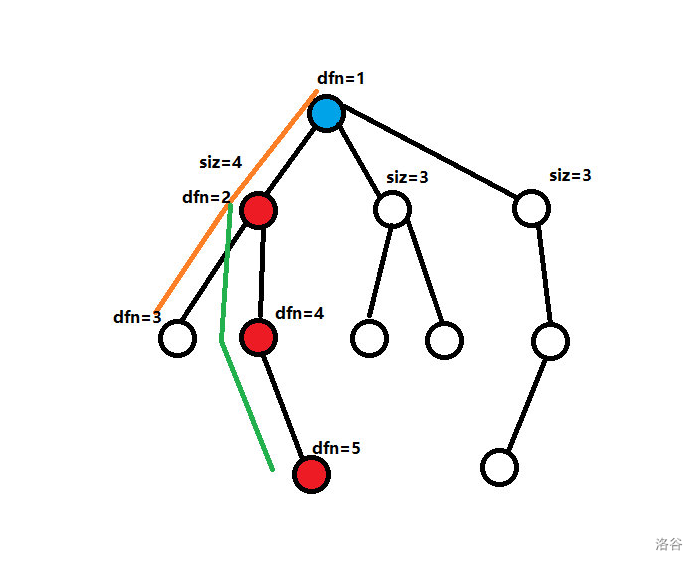
首先讲一下,为什么要先搜重儿子。因为我们要维护的是重链,而一条链的要求必须是连续的,而我们维护时使用数据结构,必然是要将它转换到数列上来做
的,如何转换呢?最好的方法就是按照 dfs 序,此时如果不先搜重儿子的话,重链上的 dfs 序就可能会断掉,如下图(橙、绿线是 dfs 搜索顺序):
如何维护
这一节很简单,没什么好讲的,因为要维护的是链,而且我们现在已经保证链上的 dfs 序连续了,所以我们直接取结点的 top 到它自己这一段进行修改或查询(即使用 dfs 序修改),然后再将当前结点跳到它 top 的 fa 即可。为了防止一个结点无限往上跳,我们先选 top 比较深的那个结点进行修改/查询,再往上跳,就可以防止无限跳的情况了。而如果选的是浅的,而它又往上跳,则深度越来越浅,必然会无限跳,最终死循环。
最后,这两个结点一定会到一条链上,而且必然有一个点会是 LCA,我们最后进行一次操作即可。
至于为什么是跳到 top 的 fa,因为 top 已经被修改/查询过了,跳到上一个结点防止重复操作。
以下就是题目+code
【模板】轻重链剖分/树链剖分
题目描述
如题,已知一棵包含 \(N\) 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
-
1 x y z,表示将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)。 -
2 x y,表示求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和。 -
3 x z,表示将以 \(x\) 为根节点的子树内所有节点值都加上 \(z\)。 -
4 x表示求以 \(x\) 为根节点的子树内所有节点值之和
输入格式
第一行包含 \(4\) 个正整数 \(N,M,R,P\),分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含 \(N\) 个非负整数,分别依次表示各个节点上初始的数值。
接下来 \(N-1\) 行每行包含两个整数 \(x,y\),表示点 \(x\) 和点 \(y\) 之间连有一条边(保证无环且连通)。
接下来 \(M\) 行每行包含若干个正整数,每行表示一个操作。
输出格式
输出包含若干行,分别依次表示每个操作 \(2\) 或操作 \(4\) 所得的结果(对 \(P\) 取模)。
样例 #1
样例输入 #1
5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3
样例输出 #1
2
21
提示
【数据规模】
对于 \(30\%\) 的数据: \(1 \leq N \leq 10\),\(1 \leq M \leq 10\);
对于 \(70\%\) 的数据: \(1 \leq N \leq {10}^3\),\(1 \leq M \leq {10}^3\);
对于 \(100\%\) 的数据: \(1\le N \leq {10}^5\),\(1\le M \leq {10}^5\),\(1\le R\le N\),\(1\le P \le 2^{31}-1\)。
【样例说明】
树的结构如下:
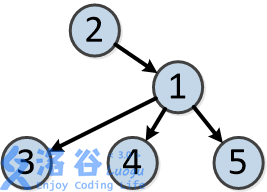
各个操作如下:
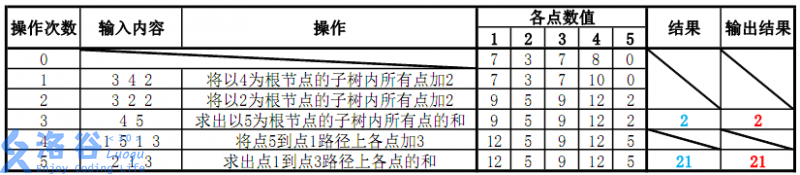
故输出应依次为 \(2\) 和 \(21\)。
------------------------------------------------
code
#include<bits/stdc++.h>
#define lson pos<<1
#define rson pos<<1|1
#define int long long
using namespace std;
const int N=1e5+5;
struct node1{
int next,v;
}e[N<<1];
struct node2{
int lazy,sum,len;
}tree[N<<2];
int head[N],dep[N],f[N],Size[N],son[N],w[N],dfn[N],top[N],pre[N];
int num,cnt,n,m,r,mod;
inline void add(int u,int v)
{
num++;
e[num].v=v;
e[num].next=head[u];
head[u]=num;
}
inline void dfs1(int now,int fa)
{
dep[now]=dep[fa]+1;
Size[now]=1;
f[now]=fa;
for(int i=head[now];i;i=e[i].next)
{
int v=e[i].v;
if(v==fa) continue;
dfs1(v,now);
Size[now]+=Size[v];
if(Size[v]>Size[son[now]]) son[now]=v;
}
}
inline void dfs2(int now,int topp)
{
dfn[now]=++cnt;
top[now]=topp;
pre[cnt]=now;
if(son[now]) dfs2(son[now],topp) ;
for(int i=head[now];i;i=e[i].next)
{
int v=e[i].v;
if(v==f[now] || v==son[now]) continue;
dfs2(v,v);
}
}
inline void built(int pos,int l,int r)
{
tree[pos].len=r-l+1;
if(l==r)
{
tree[pos].sum=w[pre[l]]%mod;
tree[pos].lazy=0;
return ;
}
int mid=l+r>>1;
built(lson,l,mid);
built(rson,mid+1,r);
tree[pos].sum=(tree[lson].sum+tree[rson].sum)%mod;
}
inline void push_down(int pos)
{
if(!tree[pos].lazy) return ;
tree[lson].lazy+=tree[pos].lazy%mod;
tree[rson].lazy+=tree[pos].lazy%mod;
tree[lson].sum+=tree[lson].len*tree[pos].lazy%mod;
tree[rson].sum+=tree[rson].len*tree[pos].lazy%mod;
tree[pos].lazy=0;
}
inline int query(int pos,int l,int r,int L,int R)
{
int res=0;
if(l>=L and r<=R) return tree[pos].sum%mod;
push_down(pos);
int mid=l+r>>1;
if(L<=mid) res+=query(lson,l,mid,L,R)%mod;
if(R>mid) res+=query(rson,mid+1,r,L,R)%mod;
return res;
}
void update(int pos,int l,int r,int L,int R,int v)
{
if(l>=L and r<=R)
{
tree[pos].lazy+=v;
tree[pos].sum+=v*tree[pos].len;
return ;
}
push_down(pos);
int mid=l+r>>1;
if(L<=mid) update(lson,l,mid,L,R,v);
if(R>mid) update(rson,mid+1,r,L,R,v);
tree[pos].sum=(tree[lson].sum+tree[rson].sum)%mod;
}
inline int Find(int x,int y)
{
int Ans=0;
int Top1=top[x],Top2=top[y];
while(Top1!=Top2)
{
if(dep[Top1]<dep[Top2])
{
swap(Top1,Top2);
swap(x,y);
}
Ans+=query(1,1,n,dfn[Top1],dfn[x]);
x=f[Top1],Top1=top[x];
}
if(dep[x]>dep[y]) swap(x,y);
Ans+=query(1,1,n,dfn[x],dfn[y])%mod;
return Ans;
}
inline void change(int x,int y,int v)
{
int Top1=top[x],Top2=top[y];
while(Top1!=Top2)
{
if(dep[Top1]<dep[Top2])
{
swap(Top1,Top2);
swap(x,y);
}
update(1,1,n,dfn[Top1],dfn[x],v);
x=f[Top1],Top1=top[x];
}
if(dep[x]>dep[y]) swap(x,y);
update(1,1,n,dfn[x],dfn[y],v);
}
signed main()
{
scanf("%lld%lld%lld%lld",&n,&m,&r,&mod);
for(int i=1;i<=n;++i) scanf("%lld",&w[i]);
for(int i=1;i<n;++i)
{
int u,v;
scanf("%lld%lld",&u,&v);
add(u,v);add(v,u);
}
dfs1(r,0);dfs2(r,r);
built(1,1,n);
for(int i=1;i<=m;++i)
{
int opt;
scanf("%lld",&opt);
if(opt==1)
{
int x,y,z;
scanf("%lld%lld%lld",&x,&y,&z);
change(x,y,z);
}
if(opt==2)
{
int x,y;
scanf("%lld%lld",&x,&y);
printf("%lld\n",(Find(x,y))%mod);
}
if(opt==3)
{
int x,z;
scanf("%lld%lld",&x,&z);
update(1,1,n,dfn[x],dfn[x]+Size[x]-1,z);
}
if(opt==4)
{
int x;
scanf("%lld",&x);
printf("%lld\n",(query(1,1,n,dfn[x],dfn[x]+Size[x]-1))%mod);
}
}
return 0;
}
小小例题 P1505 [国家集训队]旅游
[国家集训队]旅游
题目背景
Ray 乐忠于旅游,这次他来到了 T 城。T 城是一个水上城市,一共有 \(n\) 个景点,有些景点之间会用一座桥连接。为了方便游客到达每个景点但又为了节约成本,T 城的任意两个景点之间有且只有一条路径。换句话说, T 城中只有 \(n-1\) 座桥。
Ray 发现,有些桥上可以看到美丽的景色,让人心情愉悦,但有些桥狭窄泥泞,令人烦躁。于是,他给每座桥定义一个愉悦度 \(w\),也就是说,Ray 经过这座桥会增加 \(w\) 的愉悦度,这或许是正的也可能是负的。有时,Ray 看待同一座桥的心情也会发生改变。
现在,Ray 想让你帮他计算从 \(u\) 景点到 \(v\) 景点能获得的总愉悦度。有时,他还想知道某段路上最美丽的桥所提供的最大愉悦度,或是某段路上最糟糕的一座桥提供的最低愉悦度。
题目描述
给定一棵 \(n\) 个节点的树,边带权,编号 \(0 \sim n-1\),需要支持五种操作:
C i w将输入的第 \(i\) 条边权值改为 \(w\)N u v将 \(u,v\) 节点之间的边权都变为相反数SUM u v询问 \(u,v\) 节点之间边权和MAX u v询问 \(u,v\) 节点之间边权最大值MIN u v询问 \(u,v\) 节点之间边权最小值
保证任意时刻所有边的权值都在 \([-1000,1000]\) 内。
输入格式
第一行一个正整数 \(n\),表示节点个数。
接下来 \(n-1\) 行,每行三个整数 \(u,v,w\),表示 \(u,v\) 之间有一条权值为 \(w\) 的边,描述这棵树。
然后一行一个正整数 \(m\),表示操作数。
接下来 \(m\) 行,每行表示一个操作。
输出格式
对于每一个询问操作,输出一行一个整数表示答案。
样例 #1
样例输入 #1
3
0 1 1
1 2 2
8
SUM 0 2
MAX 0 2
N 0 1
SUM 0 2
MIN 0 2
C 1 3
SUM 0 2
MAX 0 2
样例输出 #1
3
2
1
-1
5
3
提示
【数据范围】
对于 \(100\%\) 的数据,\(1\le n,m \le 2\times 10^5\)。
2020.02.04 修正了一点数据的错误
2020.03.14 加入了一组 hack 数据
2020.11.26 加入了一组 hack 数据 By @_Leaving
/*
work by Low_key_smile
change by LKawaii
2022.7.25 水紫
*/
#include<bits/stdc++.h>
#define k pos
#define lson pos<<1
#define rson pos<<1|1
using namespace std;
const int N=2e5+5;
const int INF=0x3f3f3f3f;
inline int read()
{
int s=0,w=1;char ch=getchar();
while(ch<'0'||ch>'9')
{ if(ch=='-') w=-1; ch=getchar();}
while(ch>='0'&&ch<='9')
{ s=s*10+ch-'0'; ch=getchar();}
return s*w;
}
inline void write(int x) {if (x < 0) putchar('-'), x = -x; if(x > 9) write(x / 10); putchar(x % 10 + '0');}
struct node1{
int next,v,w,u;
}e[N<<1];
struct node2{
int lazy,sum,len,mx,mi;
}tree[N<<2];
int head[N],dep[N],f[N],Size[N],son[N],w[N],dfn[N],top[N],pre[N];
int num,cnt,n,m,r, U[N],V[N];
inline void add(int u,int v,int w)
{
num++;
e[num].v=v;
e[num].w=w;
e[num].u=u;
e[num].next=head[u];
head[u]=num;
}
//'''''''''''''''''''''''''''''''''''''''''''''''线段树
inline void built(int pos,int l,int r)
{
tree[pos].len=r-l+1;
if(l==r)
{
tree[pos].mi=tree[pos].mx=tree[pos].sum=w[pre[l]];
tree[pos].lazy=0;
return ;
}
int mid=l+r>>1;
built(lson,l,mid);
built(rson,mid+1,r);
tree[pos].sum=(tree[lson].sum+tree[rson].sum);
tree[pos].mx=max(tree[lson].mx,tree[rson].mx);
tree[pos].mi=min(tree[lson].mi,tree[rson].mi);
}
inline void push_down(int pos)
{
if(!tree[pos].lazy) return ;
tree[lson].lazy^=1;
tree[lson].sum=-tree[lson].sum;
tree[lson].mx=-tree[lson].mx;
tree[lson].mi=-tree[lson].mi;
swap(tree[lson].mx,tree[lson].mi);
tree[rson].lazy^=1;
tree[rson].sum=-tree[rson].sum;
tree[rson].mx=-tree[rson].mx;
tree[rson].mi=-tree[rson].mi;
swap(tree[rson].mx,tree[rson].mi);
tree[pos].lazy=0;
}
inline int query(int pos,int l,int r,int L,int R)
{
int res=0;
if(l>=L and r<=R) return tree[pos].sum;
push_down(pos);
int mid=l+r>>1;
if(L<=mid) res+=query(lson,l,mid,L,R);
if(R>mid) res+=query(rson,mid+1,r,L,R);
return res;
}
int Sum(int pos,int l,int r,int L,int R)
{
int res=0;
if(l>=L and r<=R) return tree[pos].sum;
push_down(pos);
int mid=l+r>>1;
if(L<=mid) res+=Sum(lson,l,mid,L,R);
if(R>mid) res+=Sum(rson,mid+1,r,L,R);
return res;
}
int Max(int pos,int l,int r,int L,int R)
{
int res=-INF;
if(l>=L and r<=R) return tree[pos].mx;
push_down(pos);
int mid=l+r>>1;
if(L<=mid) res=max(res,Max(lson,l,mid,L,R));
if(R>mid) res=max(res,Max(rson,mid+1,r,L,R));
return res;
}
int Min(int pos,int l,int r,int L,int R)
{
int res=INF;
if(l>=L and r<=R) return tree[pos].mi;
push_down(pos);
int mid=l+r>>1;
if(L<=mid) res=min(res,Min(lson,l,mid,L,R));
if(R>mid) res=min(res,Min(rson,mid+1,r,L,R));
return res;
}
void update(int k,int l,int r,int x,int v)
{
if(l==r)
{
tree[k].sum=tree[k].mx=tree[k].mi=v;
return ;
}
push_down(k);
int mid=(l+r)>>1;
if(x<=mid) update(lson,l,mid,x,v);
else update(rson,mid+1,r,x,v);
tree[pos].sum=(tree[lson].sum+tree[rson].sum);
tree[pos].mx=max(tree[lson].mx,tree[rson].mx);
tree[pos].mi=min(tree[lson].mi,tree[rson].mi);
push_down(pos);
}
void change(int k,int l,int r,int L,int R)
{
if(l>=L&&r<=R)
{
tree[k].lazy^=1;
tree[k].mx=-tree[k].mx;
tree[k].mi=-tree[k].mi;
tree[k].sum=-tree[k].sum;
swap(tree[k].mx,tree[k].mi);
return ;
}
push_down(k);
int mid=(l+r)>>1;
if(L<=mid) change(lson,l,mid,L,R);
if(R>mid) change(rson,mid+1,r,L,R);
tree[pos].sum=(tree[lson].sum+tree[rson].sum);
tree[pos].mx=max(tree[lson].mx,tree[rson].mx);
tree[pos].mi=min(tree[lson].mi,tree[rson].mi);
}
//''''''''''''''''''''''''''''''''''''''''''''''''线段树
//````````````````````````````````````````树剖
inline int Qsum(int x,int y)
{
int Ans=0;
int Top1=top[x],Top2=top[y];
while(Top1!=Top2)
{
if(dep[Top1]<dep[Top2])
{
swap(Top1,Top2);
swap(x,y);
}
Ans+=Sum(1,1,n,dfn[Top1],dfn[x]);
x=f[Top1],Top1=top[x];
}
if(x!=y){
if(dep[x]>dep[y]) swap(x,y);
Ans+=Sum(1,1,n,dfn[x]+1,dfn[y]);
}
return Ans;
}
inline int Qmax(int x,int y)
{
int Ans=-INF;
int Top1=top[x],Top2=top[y];
while(Top1!=Top2)
{
if(dep[Top1]<dep[Top2])
{
swap(Top1,Top2);
swap(x,y);
}
Ans=max(Ans,Max(1,1,n,dfn[Top1],dfn[x]));
x=f[Top1],Top1=top[x];
}
if(x!=y){
if(dep[x]>dep[y]) swap(x,y);
Ans=max(Ans,Max(1,1,n,dfn[x]+1,dfn[y]));
}
return Ans;
}
inline int Qmin(int x,int y)
{
int Ans=INF;
int Top1=top[x],Top2=top[y];
while(Top1!=Top2)
{
if(dep[Top1]<dep[Top2])
{
swap(Top1,Top2);
swap(x,y);
}
Ans=min(Ans,Min(1,1,n,dfn[Top1],dfn[x]));
x=f[Top1],Top1=top[x];
}
if(x!=y){
if(dep[x]>dep[y]) swap(x,y);
Ans=min(Ans,Min(1,1,n,dfn[x]+1,dfn[y]));
}
return Ans;
}
void changes(int x,int y)
{
int top1=top[x],top2=top[y];
while(top1!=top2)
{
if(dep[top1]<dep[top2])
{
swap(top1,top2);
swap(x,y);
}
change(1,1,n,dfn[top1],dfn[x]);
x=f[top1],top1=top[x];
}
if(x!=y){
if(dep[x]>dep[y]) swap(x,y);
change(1,1,n,dfn[x]+1,dfn[y]);
}
}
//```````````````````````````````````````````树剖
//'''''''''''''''''''''''''''''''''''''''''''''
inline void dfs1(int now,int fa)
{
dep[now]=dep[fa]+1;
Size[now]=1;
f[now]=fa;
for(int i=head[now];i;i=e[i].next)
{
int v=e[i].v;
if(v==fa) continue;
w[v]=e[i].w;
dfs1(v,now);
Size[now]+=Size[v];
if(Size[v]>Size[son[now]]) son[now]=v;
}
}
inline void dfs2(int now,int topp)
{
dfn[now]=++cnt;
top[now]=topp;
pre[cnt]=now;
if(!son[now]) return ;
dfs2(son[now],topp) ;
for(int i=head[now];i;i=e[i].next)
{
int v=e[i].v;
if(v==f[now] || v==son[now]) continue;
dfs2(v,v);
}
}
//'''''''''''''''''''''''''''''''''''''''''''''''''
signed main()
{
// freopen("P1505_1.in","r",stdin);
// freopen("Pceshi.out","w",stdout);
n=read();
for(int i=1;i<n;++i)
{
int u=read(),v=read(),w=read();
u++,v++;
add(u,v,w),add(v,u,w);
U[i]=u,V[i]=v;
}
dfs1(1,0);
dfs2(1,1);
built(1,1,n);
m=read();
for(int i=1;i<=m;++i)
{
string s;
cin>>s;
if(s[0]=='C')
{
int x=read(),w=read();
int u=U[x],v=V[x];
if(dep[u]<dep[v]) swap(u,v);
update(1,1,n,dfn[u],w);
}
if(s[0]=='N')
{
int u=read(),v=read();
u++,v++;
changes(u,v);
}
if(s[0]=='S')
{
int u=read(),v=read();
u++,v++;
write(Qsum(u,v));
putchar('\n');
}
if(s[0]=='M'&&s[1]=='A')
{
int u=read(),v=read();
u++,v++;
write(Qmax(u,v));
putchar('\n');
}
if(s[0]=='M'&&s[1]=='I')
{
int u=read(),v=read();
u++,v++;
write(Qmin(u,v));
putchar('\n');
}
}
return 0;
}
解释:
1.本题最重点的地方:边权转点权
dalao的解释
这个题是一个边转点的树剖,由于一个点有一个父亲,多个儿子,所以一个点的权值代表的是它父亲和它之间的边的权值,如果你查询 $dfn[x]$,$dfn[y]$ 就会多出一条不在链上的边
if(x!=y){
if(dep[x]>dep[y]) swap(x,y);
change(1,1,n,dfn[x]+1,dfn[y]);//this的+1就是处理的
}
我的解释:(我看不懂,所以我来解释一下
因为边权转点权就是把当前的点的边权落到下面的电上,所以搜的的时候如果直接搜索dfn[x]-dfn[y]会多出一条边,也就是现在的靠上的点的边权,而实际上这个点的边权是不用计算的,又因为是在同一重链上,所以dfn序是连续的,只需要+1就能到下面的点上
就比如说这张图,我们一看就知道标记黑色的是重链,举个栗子,先来看左半部分如果求11-12之前的值,就需要先找到他们两者的Top也就是顶端,然后11找到了2 ,12找到了12,我们就可以直接加上12,因为现在11和12不在同一节点,(也可以这么理解:这道题是边权下沉,边权下沉的话12节点刚刚好就可以承接到6-12之间的价值,就不需要减去了),然后12号带你继续跳边,跳的6号,好,现在两个节点都在同一条链上了就要注意了,交换完之后,因为边权是下沉的,所以顶端的点就要往下移一位,否则会找到多余的边,就比如现在的x在2号节点,因为2号节点的边权是记录的上面的9,所以说只需要下沉一个就可以愉快的记录一下2号节点下面的10边了,然后求的就是1号节点到11号节点的价值了
2.由于根节点是 0 ,所以加边的时候直接 \(u++\) ,\(v++\)
3.有几个可能错的地方:
1)修改 \(tag\) 不要直接赋值为 1
2)最小值和最大值取反后要 \(swap\) 一下
2)单点修改、区间修改都要下传标记
结尾我放一个线段树的模板吧
话说线段树不会的就退役吧
#include<bits/stdc++.h>
#define int long long
#define lson pos<<1
#define rson pos<<1|1
using namespace std;
const int N=1e6;
int n,m;
struct node{
int lazy,sum,len;
}tree[N<<1];
void built(int pos,int l,int r)
{
//cout<<1<<endl;
tree[pos].len=r-l+1;
if(l==r)
{
cin>>tree[pos].sum;
return ;
}
int mid=l+r>>1;
built(lson,l,mid);
built(rson,mid+1,r);
tree[pos].sum=tree[lson].sum+tree[rson].sum;
}
void down(int pos)
{
if(!tree[pos].lazy) return ;
tree[lson].lazy += tree[pos].lazy;
tree[rson].lazy += tree[pos].lazy;
tree[lson].sum += tree[lson].len * tree[pos].lazy;
tree[rson].sum += tree[rson].len * tree[pos].lazy;
tree[pos].lazy=0;
}
void add(int pos,int l,int r,int L,int R,int k)
{
if(l>=L and r<=R)
{
tree[pos].sum += k * tree[pos].len;
tree[pos].lazy += k;
return ;
}
down(pos) ; int mid=l+r>>1;
if(L<=mid) add(lson,l,mid,L,R,k);
if(R>mid) add(rson,mid+1,r,L,R,k);
tree[pos].sum=tree[lson].sum+tree[rson].sum;
}
int query(int pos,int l,int r,int L,int R)
{
if(l>=L and r<=R)
{
return tree[pos].sum;
}
down(pos); int mid=l+r>>1,res=0;
if(L<=mid) res+=query(lson,l,mid,L,R);
if(R>mid) res+=query(rson,mid+1,r,L,R);
return res;
}
signed main()
{
ios::sync_with_stdio(false);
cin>>n>>m;
//cout<<2<<endl;
built(1,1,n);
for(int i=1;i<=m;i++)
{
int t;
cin>>t;
if(t==1)
{
int x,y,k;
cin>>x>>y>>k;
add(1,1,n,x,y,k);
}
else
{
int x,y;
cin>>x>>y;
cout<<query(1,1,n,x,y)<<endl;
}
}
return 0;
}
最后感谢dalao @LKawaii 的修改


 浙公网安备 33010602011771号
浙公网安备 33010602011771号