LaTex语法笔记

一个很有趣的个人博客,不信你来撩 fangzengye.com



上标命令：^{}
下标命令：_{}

如果角标为单个字符，可以不使用花括号；否则必须使用花括号。

分式命令：\frac{分子}{分母}

根式:
二次根式命令：\sqrt{表达式}
N次根式命令：\sqrt[n]{表达式}
求和命令：\sum_{k=1}^nf(x)
求和位置：右上和右下标正常表示，在求和符号下端和上端用\limits

\sum _k^m


     ∑
    
    
     k
    
   
  
  
   \sum_k
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.04971em; vertical-align: -0.29971em;"></span><span class="mop"><span class="mop op-symbol small-op" style="position: relative; top: -5e-06em;">∑</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.186398em;"><span class="" style="top: -2.40029em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight" style="margin-right: 0.03148em;">k</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.29971em;"><span class=""></span></span></span></span></span></span></span></span></span></span></p> 

\sum \limits _k^m


     ∑
    
    
     k
    
    
     m
    
   
  
  
   \sum \limits _k^m
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 2.35351em; vertical-align: -1.00211em;"></span><span class="mop op-limits"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.3514em;"><span class="" style="top: -2.09789em; margin-left: 0em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight" style="margin-right: 0.03148em;">k</span></span></span><span class="" style="top: -3em;"><span class="pstrut" style="height: 3em;"></span><span class=""><span class="mop op-symbol small-op">∑</span></span></span><span class="" style="top: -3.95em; margin-left: 0em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">m</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 1.00211em;"><span class=""></span></span></span></span></span></span></span></span></span></p>

积分命令：\int_a^bf(x)
上划线命令： \overline{公式}
下划线命令：\underline{公式}
上花括弧命令：\overbrace{公式}{说明}
下花括弧命令：\underbrace{公式}_{说明}
帽子符号\hat{a} \check{a} \breve{a} \tilde{a} \bar{a} \vec{a} \acute{a} \grave{a} \mathring{a} \dot{a} \ddot{a}

矩阵

$$
  \begin{matrix}
   1 & 2 & 3 \\
   4 & 5 & 6 \\
   7 & 8 & 9
  \end{matrix} \tag{1}
$$

带花括号矩阵

$$
 \left\{
 \begin{matrix}
   1 & 2 & 3 \\
   4 & 5 & 6 \\
   7 & 8 & 9
  \end{matrix}
  \right\} \tag{2}
$$

带中括号的矩阵

$$
 \left[
 \begin{matrix}
   1 & 2 & 3 \\
   4 & 5 & 6 \\
   7 & 8 & 9
  \end{matrix}
  \right] \tag{3}
$$

简约写法：
中括号

$$
 \begin{bmatrix}
   1 & 2 & 3 \\
   4 & 5 & 6 \\
   7 & 8 & 9
  \end{bmatrix} 
$$

花括号

$$
 \begin{Bmatrix}
   1 & 2 & 3 \\
   4 & 5 & 6 \\
   7 & 8 & 9
  \end{Bmatrix} \tag{5}
$$

tag（）是右侧公式代号

带省略号矩阵

\cdots ⋯
\ddots ⋱
\vdots ⋮

$$
\left[
\begin{matrix}
 1      & 2      & \cdots & 4      \\
 7      & 6      & \cdots & 5      \\
 \vdots & \vdots & \ddots & \vdots \\
 8      & 9      & \cdots & 0      \\
\end{matrix}
\right]
$$`

结果：

     [
    
    
     
      
       
        
         1
        
       
      
      
       
        
         2
        
       
      
      
       
        
         ⋯
        
       
      
      
       
        
         4
        
       
      
     
     
      
       
        
         7
        
       
      
      
       
        
         6
        
       
      
      
       
        
         ⋯
        
       
      
      
       
        
         5
        
       
      
     
     
      
       
        
         ⋮
        
        
         
        
       
      
      
       
        
         ⋮
        
        
         
        
       
      
      
       
        
         ⋱
        
       
      
      
       
        
         ⋮
        
        
         
        
       
      
     
     
      
       
        
         8
        
       
      
      
       
        
         9
        
       
      
      
       
        
         ⋯
        
       
      
      
       
        
         0
        
       
      
     
    
    
     ]
    
   
   
     \left[ \begin{matrix} 1 &amp; 2 &amp; \cdots &amp; 4 \\ 7 &amp; 6 &amp; \cdots &amp; 5 \\ \vdots &amp; \vdots &amp; \ddots &amp; \vdots \\ 8 &amp; 9 &amp; \cdots &amp; 0 \\ \end{matrix} \right] 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 5.46em; vertical-align: -2.48em;"></span><span class="minner"><span class="mopen"><span class="delimsizing mult"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 2.95301em;"><span class="" style="top: -1.34999em;"><span class="pstrut" style="height: 3.155em;"></span><span class="delimsizinginner delim-size4"><span class="">⎣</span></span></span><span class="" style="top: -2.50499em;"><span class="pstrut" style="height: 3.155em;"></span><span class="delimsizinginner delim-size4"><span class="">⎢</span></span></span><span class="" style="top: -3.10599em;"><span class="pstrut" style="height: 3.155em;"></span><span class="delimsizinginner delim-size4"><span class="">⎢</span></span></span><span class="" style="top: -3.70699em;"><span class="pstrut" style="height: 3.155em;"></span><span class="delimsizinginner delim-size4"><span class="">⎢</span></span></span><span class="" style="top: -4.95301em;"><span class="pstrut" style="height: 3.155em;"></span><span class="delimsizinginner delim-size4"><span class="">⎡</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 2.45003em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mtable"><span class="col-align-c"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 2.98em;"><span class="" style="top: -5.8275em;"><span class="pstrut" style="height: 3.6875em;"></span><span class="mord"><span class="mord">1</span></span></span><span class="" style="top: -4.6275em;"><span class="pstrut" style="height: 3.6875em;"></span><span class="mord"><span class="mord">7</span></span></span><span class="" style="top: -2.7675em;"><span class="pstrut" style="height: 3.6875em;"></span><span class="mord"><span class="mord"><span class="mord">⋮</span><span class="mord rule" style="border-right-width: 0em; border-top-width: 1.5em; bottom: 0em;"></span></span></span></span><span class="" style="top: -1.5675em;"><span class="pstrut" style="height: 3.6875em;"></span><span class="mord"><span class="mord">8</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 2.48em;"><span class=""></span></span></span></span></span><span class="arraycolsep" style="width: 0.5em;"></span><span class="arraycolsep" style="width: 0.5em;"></span><span class="col-align-c"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 2.98em;"><span class="" style="top: -5.8275em;"><span class="pstrut" style="height: 3.6875em;"></span><span class="mord"><span class="mord">2</span></span></span><span class="" style="top: -4.6275em;"><span class="pstrut" style="height: 3.6875em;"></span><span class="mord"><span class="mord">6</span></span></span><span class="" style="top: -2.7675em;"><span class="pstrut" style="height: 3.6875em;"></span><span class="mord"><span class="mord"><span class="mord">⋮</span><span class="mord rule" style="border-right-width: 0em; border-top-width: 1.5em; bottom: 0em;"></span></span></span></span><span class="" style="top: -1.5675em;"><span class="pstrut" style="height: 3.6875em;"></span><span class="mord"><span class="mord">9</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 2.48em;"><span class=""></span></span></span></span></span><span class="arraycolsep" style="width: 0.5em;"></span><span class="arraycolsep" style="width: 0.5em;"></span><span class="col-align-c"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 2.98em;"><span class="" style="top: -5.64em;"><span class="pstrut" style="height: 3.5em;"></span><span class="mord"><span class="minner">⋯</span></span></span><span class="" style="top: -4.44em;"><span class="pstrut" style="height: 3.5em;"></span><span class="mord"><span class="minner">⋯</span></span></span><span class="" style="top: -2.58em;"><span class="pstrut" style="height: 3.5em;"></span><span class="mord"><span class="minner">⋱</span></span></span><span class="" style="top: -1.38em;"><span class="pstrut" style="height: 3.5em;"></span><span class="mord"><span class="minner">⋯</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 2.48em;"><span class=""></span></span></span></span></span><span class="arraycolsep" style="width: 0.5em;"></span><span class="arraycolsep" style="width: 0.5em;"></span><span class="col-align-c"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 2.98em;"><span class="" style="top: -5.8275em;"><span class="pstrut" style="height: 3.6875em;"></span><span class="mord"><span class="mord">4</span></span></span><span class="" style="top: -4.6275em;"><span class="pstrut" style="height: 3.6875em;"></span><span class="mord"><span class="mord">5</span></span></span><span class="" style="top: -2.7675em;"><span class="pstrut" style="height: 3.6875em;"></span><span class="mord"><span class="mord"><span class="mord">⋮</span><span class="mord rule" style="border-right-width: 0em; border-top-width: 1.5em; bottom: 0em;"></span></span></span></span><span class="" style="top: -1.5675em;"><span class="pstrut" style="height: 3.6875em;"></span><span class="mord"><span class="mord">0</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 2.48em;"><span class=""></span></span></span></span></span></span></span><span class="mclose"><span class="delimsizing mult"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 2.95301em;"><span class="" style="top: -1.34999em;"><span class="pstrut" style="height: 3.155em;"></span><span class="delimsizinginner delim-size4"><span class="">⎦</span></span></span><span class="" style="top: -2.50499em;"><span class="pstrut" style="height: 3.155em;"></span><span class="delimsizinginner delim-size4"><span class="">⎥</span></span></span><span class="" style="top: -3.10599em;"><span class="pstrut" style="height: 3.155em;"></span><span class="delimsizinginner delim-size4"><span class="">⎥</span></span></span><span class="" style="top: -3.70699em;"><span class="pstrut" style="height: 3.155em;"></span><span class="delimsizinginner delim-size4"><span class="">⎥</span></span></span><span class="" style="top: -4.95301em;"><span class="pstrut" style="height: 3.155em;"></span><span class="delimsizinginner delim-size4"><span class="">⎤</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 2.45003em;"><span class=""></span></span></span></span></span></span></span></span></span></span></span></span></p>

增广矩阵

$$ 
\left[
    \begin{array}{cc|c}
      1 & 2 & 3 \\
      4 & 5 & 6
    \end{array}
\right] \tag{7}
$$


        [
       
       
        
         
          
           
            1
           
          
         
         
          
           
            2
           
          
         
         
          
           
            3
           
          
         
        
        
         
          
           
            4
           
          
         
         
          
           
            5
           
          
         
         
          
           
            6
           
          
         
        
       
       
        ]
       
      
     
     
     
      
       (7)
      
     
    
   
   
     \left[ \begin{array}{cc|c} 1 &amp; 2 &amp; 3 \\ 4 &amp; 5 &amp; 6 \end{array} \right] \tag{7} 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 2.40003em; vertical-align: -0.95003em;"></span><span class="minner"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size3">[</span></span><span class="mord"><span class="mtable"><span class="arraycolsep" style="width: 0.5em;"></span><span class="col-align-c"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.45em;"><span class="" style="top: -3.61em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">1</span></span></span><span class="" style="top: -2.41em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">4</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.95em;"><span class=""></span></span></span></span></span><span class="arraycolsep" style="width: 0.5em;"></span><span class="arraycolsep" style="width: 0.5em;"></span><span class="col-align-c"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.45em;"><span class="" style="top: -3.61em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">2</span></span></span><span class="" style="top: -2.41em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">5</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.95em;"><span class=""></span></span></span></span></span><span class="arraycolsep" style="width: 0.5em;"></span><span class="vertical-separator" style="height: 2.4em; vertical-align: -0.95em;"></span><span class="arraycolsep" style="width: 0.5em;"></span><span class="col-align-c"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.45em;"><span class="" style="top: -3.61em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">3</span></span></span><span class="" style="top: -2.41em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">6</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.95em;"><span class=""></span></span></span></span></span><span class="arraycolsep" style="width: 0.5em;"></span></span></span><span class="mclose delimcenter" style="top: 0em;"><span class="delimsizing size3">]</span></span></span></span><span class="tag"><span class="strut" style="height: 2.40003em; vertical-align: -0.95003em;"></span><span class="mord text"><span class="mord">(</span><span class="mord"><span class="mord">7</span></span><span class="mord">)</span></span></span></span></span></span></span><br> 偏导符号<br> \partial<br> 求导符号<br> \mathrm{d} x<br> 点形式的求导符号：\dot x 和 \ddot y（有几个点就用几个d）<br> 全微分算子：\nabla</p>

希腊字母

小写大写语法
ααAA\alpha
ββBB\beta
γγΓΓ\gamma
δδΔΔ\delta
ϵϵEE\epsilon
ζζZZ\zeta
ννNN\nu
ξξΞΞ\xi
οοOO\omicron
ππΠΠ\pi
ρρPP\rho
σσΣΣ\sigma
ηηHH\eta
θθΘΘ\theta
ιιII\iota
κκKK\kappa
λλΛΛ\lambda
μμMM\mu
ττTT\tau
υυΥΥ\upsilon
ϕϕΦΦ\phi
χχXX\chi
ψψΨΨ\psi
ωωΩΩ\omega
ηΗ\eta

特殊符号

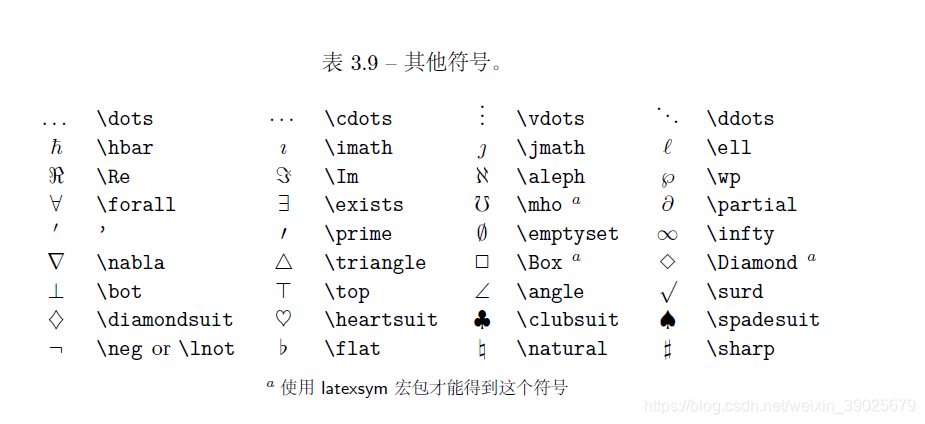
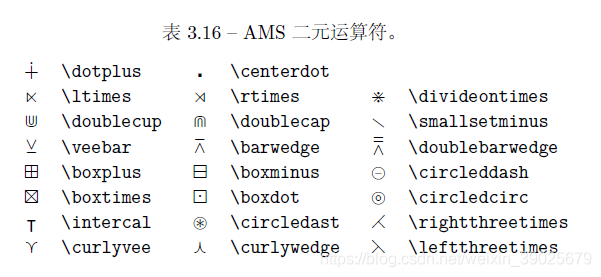
在这里插入图片描述
在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述
参考文章：

https://www.jianshu.com/p/8aa646fad1c5
https://blog.csdn.net/lanchunhui/article/details/49819445
https://blog.csdn.net/ying_xu/article/details/51240291

posted @ 2020-04-01 11:03  开源的Boy  阅读(360)  评论(0)    收藏  举报