B

题目

甲，乙，丙3人间相互传球。假设他们相互间传球是等可能的，并且由甲开始传球。
（3）猜想：经过n次传球后，球传到甲，乙，丙3人概率之间的大小关系。

解答

我们首先可以用树状图来提现（甲，乙，丙为A，B，C）：

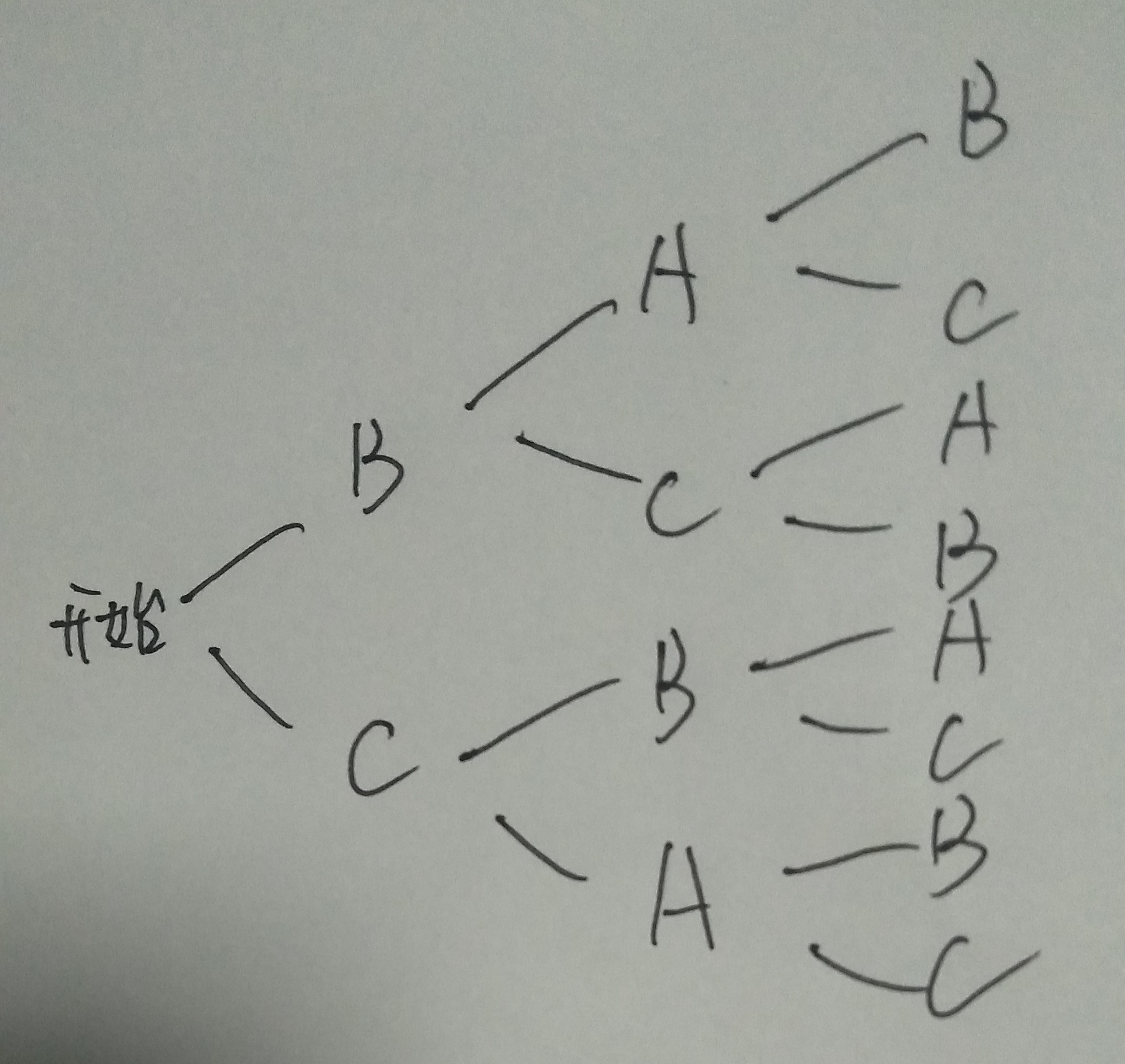
我们可以知道，对于第\(n\)次传球后，球传到某人（比如甲）的概率为：第\(n\)列中A的个数 除于 第\(n\)列的字母总个数。令\(f(x),g(x),h(x)\)分别表示第\(x\)列中A，B，C的个数。所以会有：

\[P(球到A手上)=\dfrac{f(n)}{2^n} \]

其他同理。
所以，我们会有如下等式：

\[f(x)=g(x-1)+h(x-1) \]

\[g(x)=f(x-1)+h(x-1) \]

\[h(x)=f(x-1)+g(x-1) \]

\[f(0)=1,g(0)=h(0)=0 \]

我们可以用上图明显得出，第\(x\)列的A就是由第\(x-1\)列中的B，C所有的两个分支中的一个得到，也就是前者等于后者之和。证毕。
由这些函数的定义可得等式：

\[f(x)+g(x)+h(x)=f(x)+f(x+1)=2^x \]

\[\therefore f(x)=2^x-f(x+1) \]

将最初的基本式扩展：

\[f(x)=g(x-1)+h(x-1)=f(x-2)+h(x-2)+f(x-2)+g(x-2)=2f(x-2)+f(x-1) \]

用\(f(x)=2f(x-2)+f(x-1)\)扩展，得：

\[f(x)=2[f(x-2)+f(x-3)+...+f(0)]+f(1) \]

用\(f(x)=2^x-f(x+1)\)扩展并化简，得：

\[f(x)=2(2^{x-3}+2^{x-5}+...+1)+0 \]

\[f(x)=2^{x-2}+2^{x-4}+...+2+0 \]

\[\therefore P(球第n轮后到A手上)=\dfrac{f(n)}{2^n}=\dfrac{2^{n-2}+2^{n-4}+...+2}{2^n}=\dfrac{1}{2^2}+\dfrac{1}{2^4}+\dfrac{1}{2^6}+...+\dfrac{1}{2^{n-1}} \]

其中，\(n\in[2,\infty)\bigcap n\in Z\)

当\(n=1\)时，\(P=0\)

同理，有如下等式：

\[g(x)=2[g(x-2)+g(x-3)+...+g(0)]+g(1) \]

将\(g(1)=h(0)+f(0)=1\)与\(g(x)=2^x-g(x+1)\)代入并化简，有：

\[g(x)=2^{x-2}+2^{x-4}+...+0+1 \]

\[\therefore P(球第n轮后到B手上)=\dfrac{g(n)}{2^n}=\dfrac{2^{n-2}+2^{n-4}+...+1}{2^n}=\dfrac{1}{2^2}+\dfrac{1}{2^4}+\dfrac{1}{2^6}+...+\dfrac{1}{2^{n}} \]

其中，\(n\in[1,\infty)\bigcap n\in Z\)

同理易得，\(P(球第n轮后到C手上)=P(球第n轮后到B手上)\),\(n取值范围相同\)。

很明显,\(f(n)>g(n)=h(n)\)

\[\therefore P(A)>P(B)=P(C)(n\ne 1) \]

\[P(A)<P(B)=P(C)(n=1) \]

\[n\in N* \]