训练总结 2

edu 176

D

对于固定的操作，需要花费的代价和 \(x, y\) 无关，所以可以预处理出操作的代价。\(f(i, a, b)\) 表示已经用了前 \(i\) 位，对 x，y 进行 \(2^a\) 和 \(2^b\) 操作的最小代价。

转移就是从低位向高位转移，\(f(i, j + i, k) \leftarrow f(i - 1, j, k)\)，\(f(i, j, k + i) \leftarrow f(i - 1, j, k)\)。

如何找答案：找到 x，y 二进制下从高位到低位的 LCP，对于这一段，选择 \(i\) 位和低位全部扣掉就行了。最后还要与 \(f(|x|, |y| + 1)\) 和 \(f(|x + 1|, |y|)\) 更新，其中 \(|x|, |y|\) 表示 x，y 的二进制位数。

E

gym 103483

G

首先两边等式都有 \(a_1, a_2, a_3, a_4\) 是不好处理的，所以先移项：\(a_1a_4 - a_1 - a_4 = a_2a_3 - a_2 - a_3\)。

然后有 \(xy - x - y - 1 = (x - 1)(y - 1)\)，所以相当于 \((a_1 - 1)(a_4 - 1) = (a_2 - 1)(a_3 - 1)\)。

因为要让 \(a_1a_4 + a_2 + a_3\) 尽量大，所以 \(a_1, a_2, a_3, a_4\) 取尽量大。

所以我们枚举 a 的全排列，然后每次选择固定其中的三个数，根据上述式子求第四个数，然后更新答案。注意判断 \(a_i = 0\) 的情况。

注意 \(10^{-6} / 10^{-4} = 10^{-10}\)，所以为了满足精度要求，至少要保留 10 位输出。

总结：等式两边要转化成容易固定某几项然后求剩余项的形式，注意精度问题。

H

首先想如何框出一个答案的点集：令 \(F(A) = \max_{a_i(x) \in A}\{a_i(x)\}\)，\(G(B) = \min_{b_i(x) \in B}\{b_i(x)\}\)，其中 A 是开口向上抛物线的集合，B 是开口向下的抛物线的集合。那么答案的点集就是 F 和 G 框出的公共部分。找到一个合法的点只要找到一个 x 在公共部分的水平范围内，然后 y 取 \(F(A)\) 和 \(G(B)\) 的中点就好了。

注意到 \(G(B) - F(A)\) 是凸函数，可以考虑三分求出极值点，x 取这个极值点就好了。

I

首先能进行一次猜单词的关键是若干个词里是否有字符都出现过，区分两个单词的关键是某一字符出现位置的不同，可能是个数不同，也可能是个数相同位置不同。

那么自然地想到，对于若干个串，选择一个都出现过的字符，然后按照该字符在串中位置进行分类，然后往下递归 check，类似于一个多叉树的结构。那么题目要求必胜，也就是所有子节点的状态都可以区分该状态下的串的。

总结一下做法：预处理出每个串每种字符的出现位置和次数，然后每次暴力找出都出现过的字符，然后按照出现位置分类往下递归 check，如果存在一个子状态是 0，那么该状态也是 0。

预处理是 \(nL\) 的，注意到多叉树的深度不会超过 26，每层节点数不会超过 \(\min(26, n)\)，所以状态数不会太多。

cf2085

B

如果序列中有 0，只要先把 0 通过合并变成非 0 数，最后对整个序列合并就行了。

赛时想法是把 0 的连续段合并掉，长度为 1 的连续段和相邻的非 0 数合并，很复杂。更简单的做法是，我们希望只有两个数不是 0，所以对于第 n 个数如果是 0，那么合并一次就是非 0 了，那么把前面 n - 2 个数一次性合并，得到的也是非 0 数。

思考还是要学会转换角度，从整体看可能会让问题更简单，不能思维固化了。

D

E

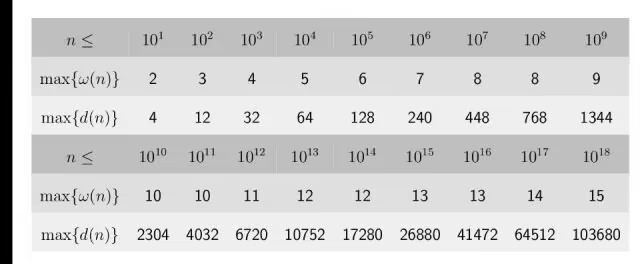
注意到 \(a_i = xk + b_i\)，所以 \(a_i - b_i\) 应该是 \(k\) 的倍数。那么 \(\sum a_i - \sum b_i\) 也是 \(k\) 的倍数，也就是说 \(k\) 只会出现在 \(\sum a_i - \sum b_i\) 的因数中。\(\sum a_i - \sum b_i\) 不会超过 \(10^{10}\)，由图可知因数个数不会超过 2304 个，所以 \(\sqrt{\sum a_i - \sum b_i}\) 找因数，对于每个因数进行 \(O(n)\) check 就好了。

cf2090

C

对于 \(t_i = 0\) 的人来说，选择空桌子是按照对角线斜向填充的，因为每次要选距离最小且 x 最小的空桌子。所以 y 方向上至少有一个人的桌子数量是 \(\sqrt{n}\) 级别的。

那么维护两个 set ：一个维护空桌子，一个维护有人的桌子。预处理把可能的桌子的坐标和距离插到 set 里。查询时每次找符合条件的元素删除就行了。

D

Lemma (Bertrand's postulate): For each positive integer \(x\), there is a prime \(p\) inside the interval \([x, 2x]\)。

E1/E2