图形学基础01

线性代数基础

单位向量

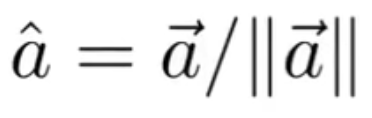
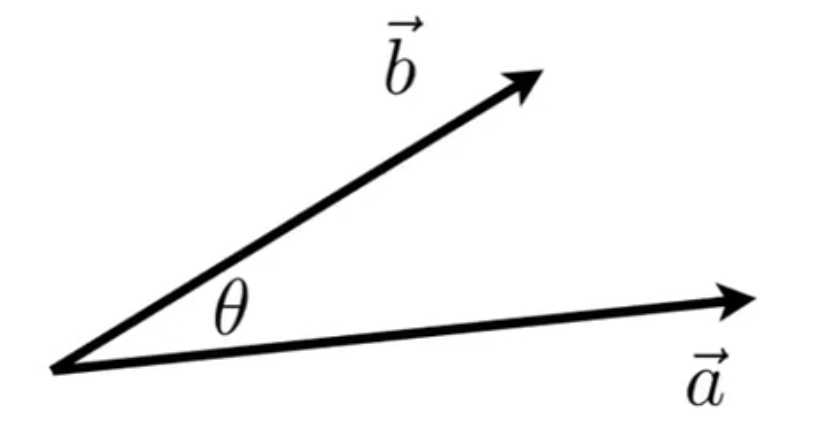
向量点积

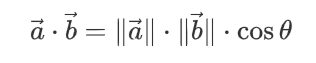
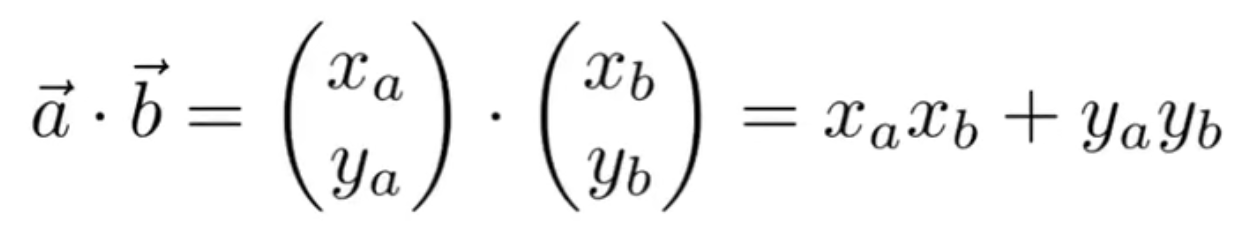
计算投影

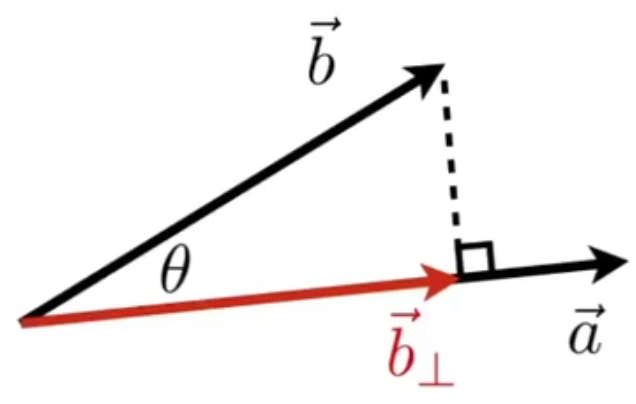
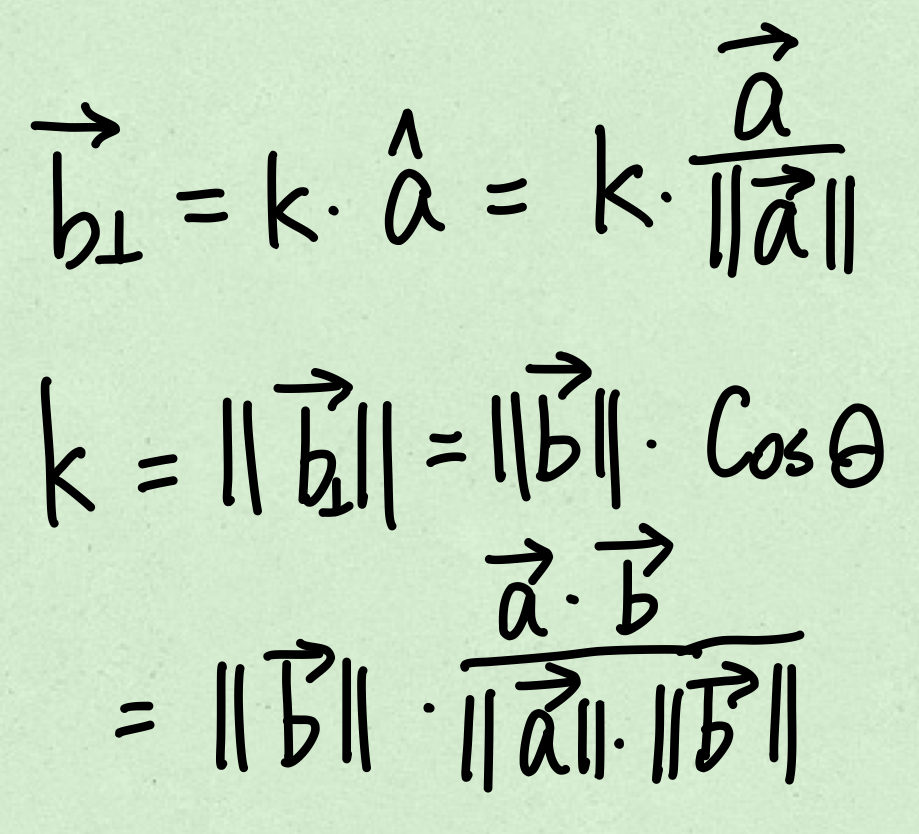
因为是B在A上的投影，所以投影向量必然是沿着A方向的

判断方向

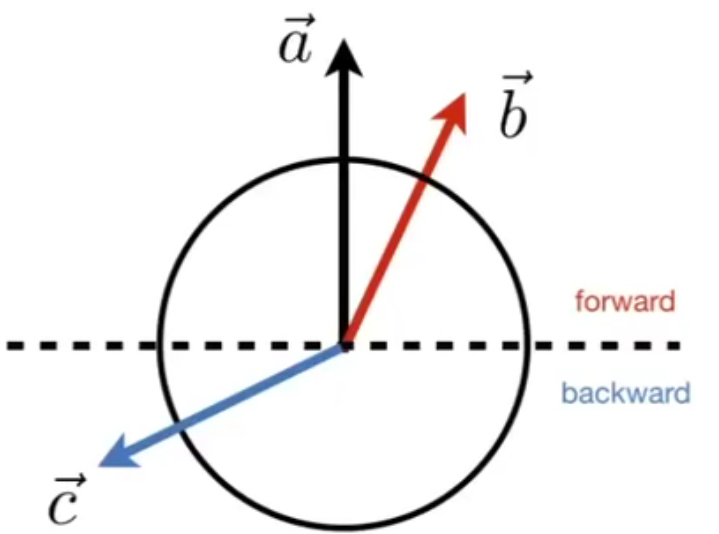
点积结果的正负，依赖于夹角的大小，当夹角大于90度时，Cos结果为负，此时可以判断两个向量朝向不同

向量叉积

两个向量叉积的结果，垂直于这两个向量，此时3个向量可以构成一个三维坐标系

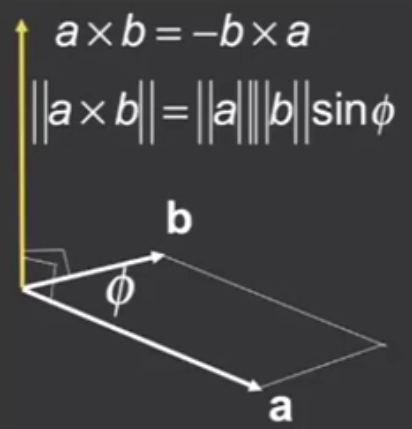
判断左右

根据右手定则以及两个向量叉积的结果的正负，很容易的可以判断这两个向量的左右关系

判断某一个点是否在三角形内

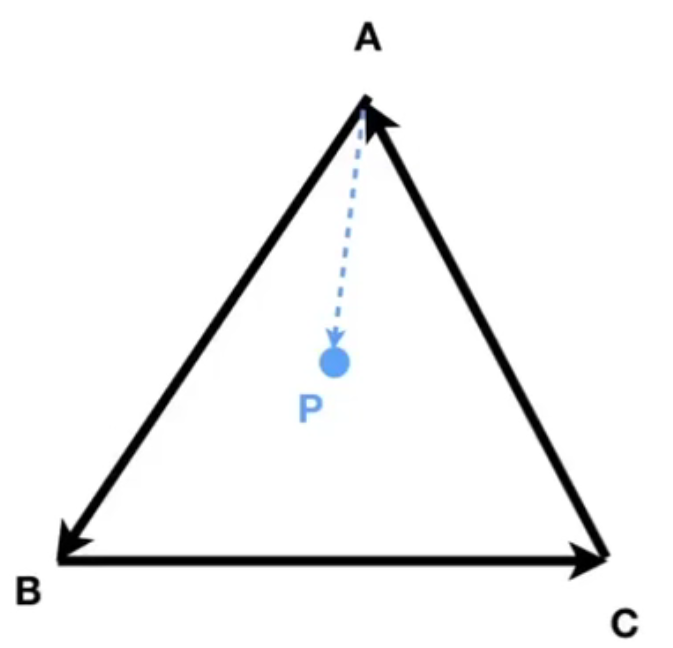
利用好上一个规则，如果P在三角形ABC内，则AP在AB的左侧，BP在BC的左侧，CP在CA的左侧，即各项叉积的结果应该都是正或者都是负

否则P不在三角形ABC内

矩阵

矩阵可以表示缩放以及选择，但没法表示平移，于是引入齐次矩阵的概念

对于一个点（X,Y,Z），我们称它对应的齐次坐标为（X,Y,Z,1）

对于一个向量（X,Y,Z），我们称它对应的齐次坐标为（X,Y,Z,0）

那么对应的矩阵也需要多加入一维，变成四维矩阵

平移矩阵：

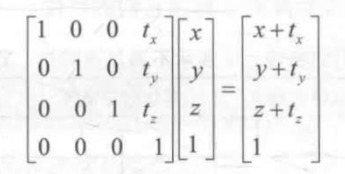
缩放矩阵：

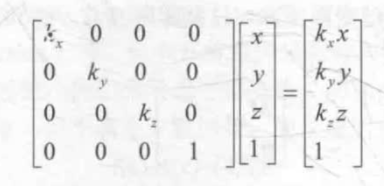
旋转矩阵则比较复杂，不多考虑，能明白齐次的概念就好

空间转换

重中之重！

一个非常关键的问题是，如果给定坐标系A下某一个点P的坐标，如何得到P在坐标系B中的坐标？

如图，假设有两个坐标系A、B，对应的基底分别是（Ua,Va）、（Ub,Vb）

其中，P在坐标系A的坐标是（x,y），如何求出P在坐标系B中的坐标？

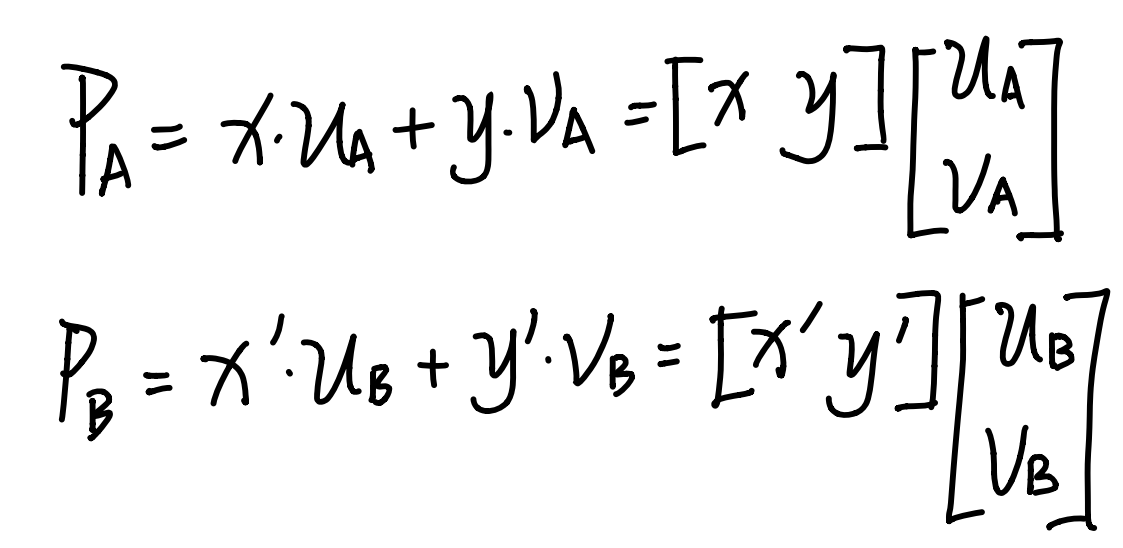
同时，我们很明显的能够发现，坐标系A的基底，可以用坐标系B来描述

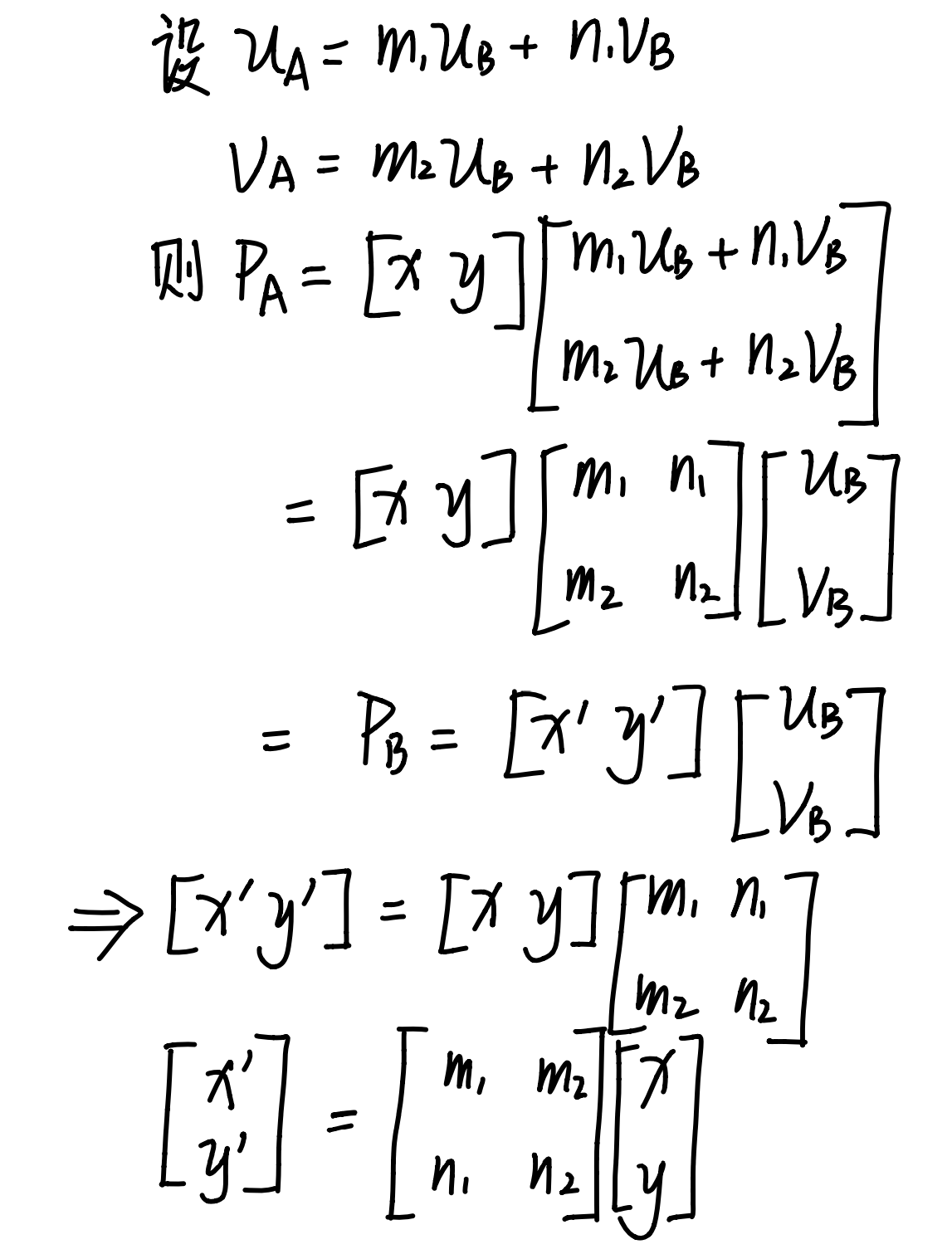
其中（m1,n1）是坐标系A的X轴的单位向量，在坐标系B中的表示，其余同理

所以只要能找到某一个坐标系的基底向量再另一个坐标系中的表示，自然就很容易能够把某一个坐标系中的点或者向量转到另一个坐标系中

此时有一个新的问题，上述两个坐标系，其坐标原点是重合的，那如果两个坐标系不在同一个位置呢？

也很容易想到，如果我们整体平移某一个坐标系，那么这个坐标系里的点或者向量，并不会发生改变

所以只要先平移子坐标系A，再利用上述规则进行转换即可

加上齐次坐标的规则，总结出三维空间中的转换公式如下：

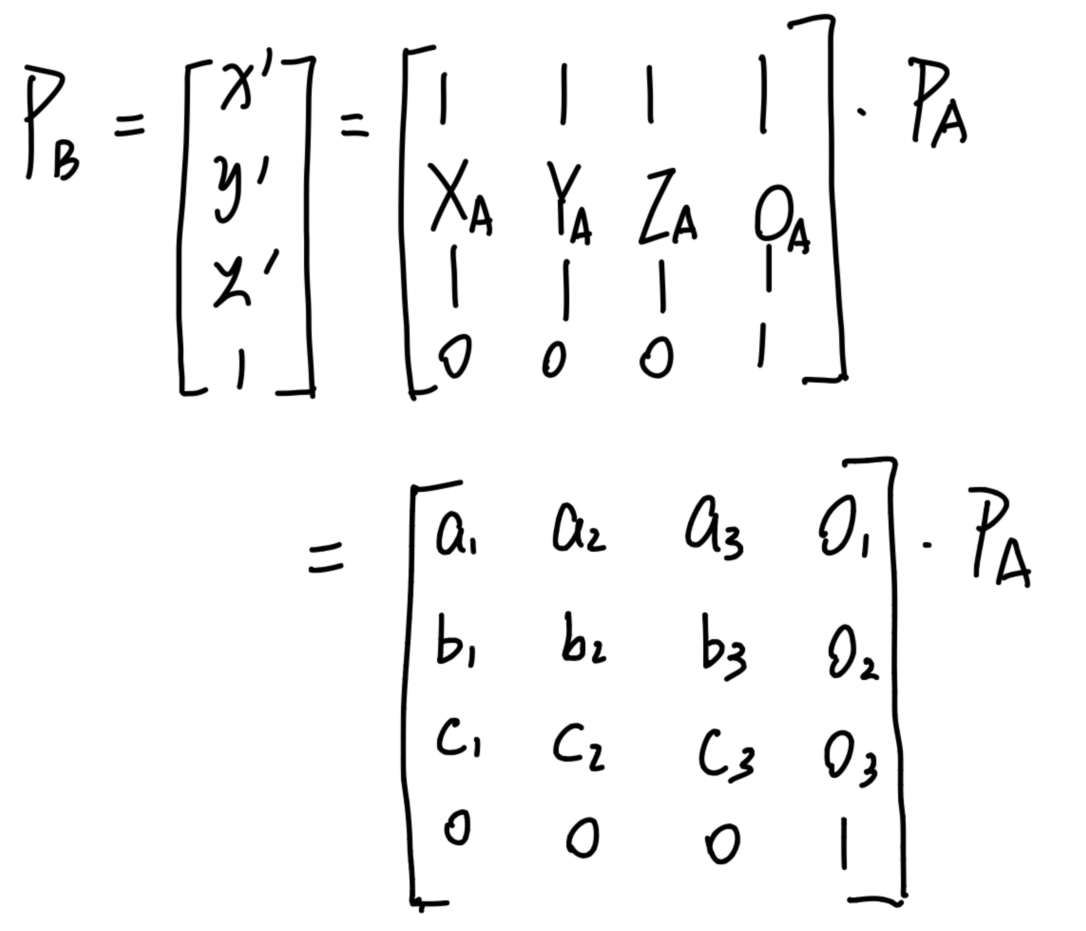
其中（Xa,Ya,Za,Oa）代表按列展开

Xa代表着坐标系A中的基底X在坐标系B中的表示，其余同理

Oa代表坐标系A的远点平移到坐标系B

坐标系

左手坐标系

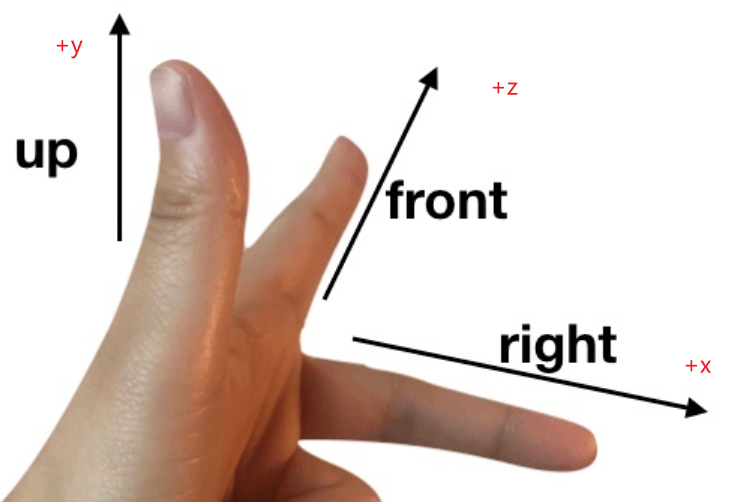
右手坐标系

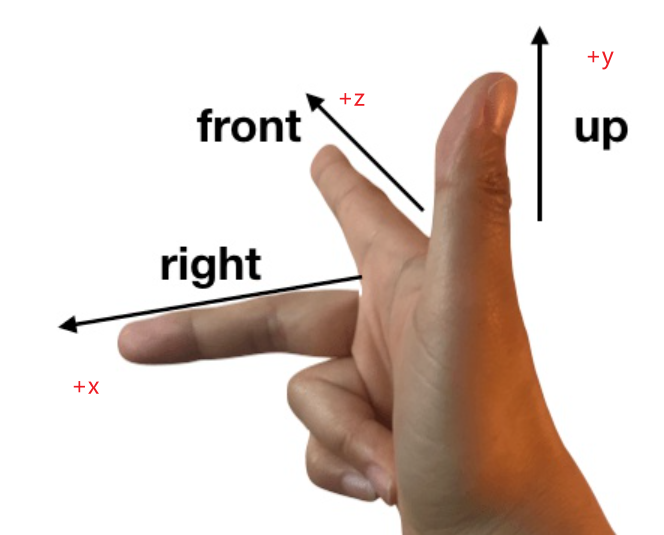
不难发现区别只是X轴的朝向不同

在Unity中，模型空间与世界空间采用左手坐标系，观察空间采用右手坐标系