LCA RMQ+ST表学习笔记

RMQ

RMQ问题：在给定的一个长度位N的区间中，有M个询问，每次询问给出区间[L,R]，求出区间段元素的

最大值/最小值。对于RMQ问题很容易想到遍历的做法，将区间[L,R]中的元素遍历一遍，即可寻找到

最大/最小值，但当区间长度较大，询问次数较多，就会耗费大量的时间。RMQ问题可以用线段树和ST

表两种做法，下面介绍ST表。

ST表法：

ST表是用来解决RMQ问题非常高效的方法，通过O(nlong)的预处理之后，可以在O(1)时间

内找到所要的答案。其中预处理就是用到了动态规划的思想。

定义：F(i,j)表示以i为下标的元素为起点，区间长度为2^j的区间最值此时区间范围是[i,i+2^j-1-1]

预处理:容易发现初始状态为 F(i,0)，此时该值表示区间[i,i]的最值，F(i,0)=a_i；

状态转移：可以将[i,j]分成长度为2^j-1的两段，一段为[i,i+2^j-1-1],另一端为[i+2^j−1,i+2^j-1]则

F(i,j)=max{f(i,j-1),f(i+2j-1,j-1)}

代码：

void ST(int n)
{
    for(int i=1;i<=n;i++)                            //预处理
        dp[i][0]=i;            
        
    for(int j=1;(1<<j)<=n;j++)
        for(int i=1;i+(1<<j)-1<=n;i++)
        {
            int a=dp[i][j-1];int b=dp[i+(1<<(j-1))][j-1];
            dp[i][j]=a<b?a:b;
        }    
}

View Code

查询操作：若查询[l,r]区间，在预处理时，每个状态对应的区间长度均为2ⁱ，给定查询区间的长度不一定为2ⁱ，

所以可以将查询区间分成两小区间，两个小区间要覆盖大区间，并且长度相等为2ⁱ，（两个区间可以重叠）。

计算时小区间长度为大区间长度取2为底的对数 k = log(l-r+1)则待查区间[l,r]可分为[l,l+2^k-1] [r-2^k+1,r]，

对应着F(l,k)和F(r-2^k+1,k),此时比较两个的值，取答案即可。

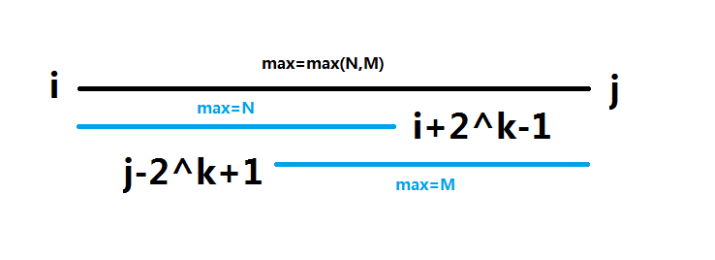
代码：

int RMQ(int l,int r)
{
    int k=0;
    while(1<<(k+1)<=r-l+1)
        k++;
    int a=dp[l][k],b=dp[r-(1<<k)+1][k];
    return a<b?a:b;
}

View Code

LCA

定义：对于有根树T的两个结点u、v，最近公共祖先LCA(T,u,v)表示一个结点x，满足x是u、v的祖先且x的深

度尽可能大（百度百科）。做法很多，这里结束以上文为基础的做法

DFS+ST表法：

思想：将树看成一个无向图，u和v的公共祖先一定在u与v之间的最短路径上，而路径中深度最小的结点，即为u，v的最近公共祖先。

算法步骤：

(1) DFS：

a:从树的根开始，将树看成一个无向图进行深度优先遍历，记录下每次到达的顶点，第一个顶点为树根root，

每经过一条边都记录它的端点，每条边都恰好经过两次.用数组ver记录结点。

b:记录first数组和deep数组，first数组记录在深度优先遍历时结点第一次出现的位置。Deep数组记录结点的深度

void dfs(int u,int dep)
{
    vis[u]=true;
    ver[++tot]=u;
    first[u]=tot;
    deep[tot]=dep;    
    for(int i=head[u];i!=-1;i=edge[i].next)
    {
        int v=edge[i].to;
        if(!vis[v])
        {
            dfs(v,dep+1);
            ver[++tot]=u;
            deep[tot]=dep;
        }
    
    }
}

View Code

可以发现当我们通过深度优先遍历记录下结点后，当我们要查询结点u，v时，我们可以在结点的数组

中找到u结点第一次出现的位置和v结点第一次出现的位置，而他们位置之间的结点便是u到v的DFS顺序

，虽然其中可能包含u或v的后代，但其中深度最小的还是u和v的最近公共祖先。因此可以用ST表记录与

结点数组相对应的深度序列的区间最小值下标,将lca转化为RMQ问题。

void ST(int n)
{
    for(int i=1;i<=n;i++)
        dp[i][0]=i;
        
    for(int j=1;(1<<j)<=n;j++)
        for(int i=1;i+(1<<j)-1<=n;i++)
        {
            int a=dp[i][j-1];int b=dp[i+(1<<(j-1))][j-1];            //记录其中结点深度最小的结点的位置
            dp[i][j]=deep[a]<deep[b]?a:b;
        }    
}

View Code

寻找LCA(u,v)时，先寻找first[u]，first[v]，将[first[u],first[v]]间的最小值的deep找出，该值下标所对应的结点即为LCA(u,v)。

即当first[u]>first[v]时，LCA(T,u,v)=RMQ(deep,R[v],R[u]),否则LCA(T,u,v) = RMQ(deep,R[u],R[v]).

int RMQ(int l,int r)
{
    int k=0;
    while(1<<(k+1)<=r-l+1)
        k++;
    int a=dp[l][k],b=dp[r-(1<<k)+1][k];
    return deep[a]<deep[b]?a:b;
}
int LCA(int u,int v)
{   
    int x=first[u],y=first[v];
    if(x>y)swap(x,y);
    int res=RMQ(x,y);
    return ver[res];
}

View Code

示例：

数组下标：　　　　 1 2 3 4 5 6 7 8 9 10 11 12 13

遍历序列：　　　　 A B D B E F E G E B A C A

结点在树中深度： 1 2 3 2 3 4 3 4 4 2 1 2 1

假设查询LCA(F,C)

1、查询F，C在序列中第一次出现的位置first[F] = 6， first[C]=12

2、去结点数组[6,12]的序列，查询与之对应的深度deep数组的最小值即

查询< 4, 3 ,4 ,4,2 ,1,2>,最小值为1，对应下标为11，即结点A，LCA(F,C)=A.

查询操作即为区间最小值，转化为RMQ即可。

例题： POJ - 1330 Nearest Common Ancestors

代码：

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int MAX=10009;
int T,n,a,b;
int head[MAX],cnt=0;
int tot=0;
int dp[MAX*2][25];                //ST表 
int deep[MAX*2];                //记录节点深度 
int ver[MAX*2];                    //记录节点编号 
int first[MAX];                    //记录点第一次出现的位置 
bool vis[MAX];    
bool isroot[MAX];                //判断根节点的数组 
struct Edge{            
    int to,next;
}edge[MAX*2];
inline void add(int u,int v)
{
    edge[cnt].to=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}
void dfs(int u,int dep)
{
    vis[u]=true;            //访问过该节点 
    ver[++tot]=u;            //将该节点记录在ver中 
    first[u]=tot;            //记录结点u第一次出现的位置 
    deep[tot]=dep;            //记录深度 
    for(int i=head[u];i!=-1;i=edge[i].next)
    {
        int v=edge[i].to;
        if(!vis[v])
        {
            dfs(v,dep+1);
            ver[++tot]=u;
            deep[tot]=dep;
        }
    
    }
} 
void ST(int n)
{
    for(int i=1;i<=n;i++)                //初始化 
        dp[i][0]=i;
        
    for(int j=1;(1<<j)<=n;j++)
        for(int i=1;i+(1<<j)-1<=n;i++)
        {
            int a=dp[i][j-1];int b=dp[i+(1<<(j-1))][j-1];        //记录其中结点序列深度最小的结点的编号 
            dp[i][j]=deep[a]<deep[b]?a:b;
        }    
}
int RMQ(int l,int r)
{
    int k=0;
    while(1<<(k+1)<=r-l+1)                    //求区间长度以二为底的对数 
        k++;
    int a=dp[l][k],b=dp[r-(1<<k)+1][k];
    return deep[a]<deep[b]?a:b;
}
int LCA(int u,int v)
{
    int x=first[u],y=first[v];
    if(x>y)swap(x,y);
    int res=RMQ(x,y);
    return ver[res];
}
void init()
{
    memset(head,-1,sizeof(head)),cnt=0;tot=0;
    memset(isroot,true,sizeof(isroot));
    memset(vis,false,sizeof(vis));
    memset(dp,0,sizeof(dp));
    memset(deep,0,sizeof(deep));
    memset(first,0,sizeof(first));
    memset(ver,0,sizeof(ver));
} 
int main()
{
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        init();
        for(int i=1;i<n;i++)
        {
            scanf("%d%d",&a,&b);
            isroot[b]=false;
            add(a,b);
            add(b,a);
        }
        int root;
        for(int i=1;i<=n;i++)
        {
            if(isroot[i])
            {
                root=i;break;
            }
        }
        dfs(root,1);
        ST(2*n-1);
        scanf("%d%d",&a,&b);
        printf("%d\n",LCA(a,b));
    }
    return 0;
}

View Code

参考：

http://dongxicheng.org/structure/lca-rmq/

https://www.cnblogs.com/YSFAC/p/7189571.html

如有错误，欢迎指出，谢谢~

posted @ 2018-11-16 21:46 _Carrot 阅读(773) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

_Carrot

LCA RMQ+ST表学习笔记

RMQ

ST表法：

代码：

LCA

DFS+ST表法：

公告