P2486 【SDOI2011】 染色

#$Description$ [题面](https://www.luogu.org/problem/P2486) 给你一颗树，有两种操作，一种是将一条链都染成一种颜色，一种是询问一条链的**颜色段个数** 比如$1122211$共有三段 #$Solution$ >线段树可支持的操作一定有区间可合并性 这道题难点设计三个地方的合并 明显树链剖分，但是线段树怎么维护呢，注意到两个区间合并时简单将贡献相加明显不对。 第一个合并是一个节点的左右儿子合并 考虑记录左右儿子左右端点的颜色编号，合并时比较左儿子右边界和右儿子左边界，如果相同则父节点贡献$-1$

第二个合并时询问时答案的合并
以上处理了该区间完整作为答案的情况，但是会有这样的情况

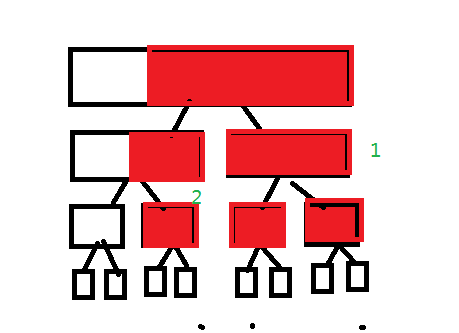
一号节点内部经过第一个合并一定是合法的，但是答案是二号节点+一号节点，他们不是一个完整区间，需要递归到二号节点，假设二号节点右边界和一号节点左边界相等，这种情况我们没有处理，就炸了。
所以我们在线段树\(query\)函数时分三种情况考虑：\(1.\)答案区间都在左子树，则递归左子树\(\ \ 2.\)都在右子树，同理\(\ \ 3.\)答案跨越\(mid\)，即在左子树和右子树，分别递归下去只可能处问题的是左儿子的右边界和右儿子的左边界（因为我们不能直接使用当前节点当答案所以第一个合并在这里无效），且答案区间一定包含这两个，记录这两个值，比较相同则\(ans--\)即可。

第三个合并是树链剖分多个区间时的合并（这也是最容易错的）
一条重链在线段树种是连续的，但一条链的这些区间在线段树中是不连续的，所以显然答案有可能出错，对于较深的那个点，用\(pos1\)记录这次线段树访问的左边界（就是在树链中靠上那个点）的颜色，访问下个线段树区间时拿这次线段树访问的左边界（在线段树询问中记录左右端点即可）和\(pos1\)比较如果相同则\(ans--\)，再用左边界更新\(pos1\)，较浅的那个点同理记录，如果交换两个点注意\(pos1,pos2\)也要交换。到最后的重链注意两个边界可能都要更新，都要判断

画张图就明白了

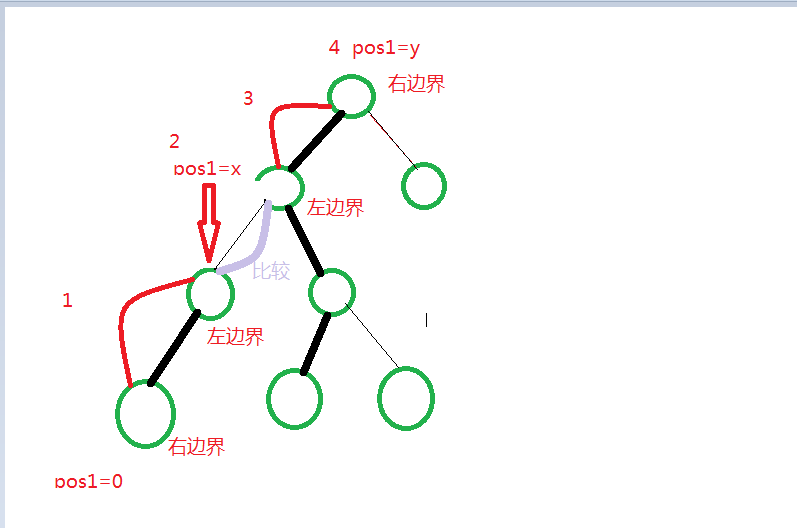
注意几点

\(1.\)树链剖分\(dfs1\)处理重儿子时尽量别用全局变量记录最大儿子的节点数,否则会剖错。
对于所有递归函数，使用全局变量一是可能被错误更新而不回溯，二是每一次每一层都要更新，更新次数太多常数大
综上尽量在递归中使用全局变量
\(2.\)对于线段树合并，不仅要考虑\(push_up\)的合并，也要考虑\(query\)时答案区间合并，还要考虑外部数据结构中线段树区间不连续时的合并，一定要考虑周全
\(3.\)对于线段树区间修改一般要使用懒标记！！！！注意\(tag\)标记别乱传，被清零再传就被\(0\)覆盖了，注意判断
细节看代码

\(Code\)

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#define maxn 200010 
#define re register
using namespace std;
inline int read()
{
	int x=0,f=1; char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
struct Edge{
	int v,nxt;
}e[maxn<<2];
char cs;
int ans;
int id[maxn],top[maxn],head[maxn],a,b,c;
int cnt,cnts,x,y,fa[maxn],siz[maxn],maxson;
int wt[maxn],tag[maxn<<2],L,R;
int dep[maxn],n,m,mson[maxn],w[maxn];
inline void add(int u,int v)
{
	e[++cnts].v=v;
	e[cnts].nxt=head[u];
	head[u]=cnts;
}
//---------------10.18线段树--------------------
#define ls p<<1
#define rs p<<1|1
struct T{
	int l,r,cl,cr,mid,val;
}tre[maxn<<2];
void push_up(int p)//注意结构体中每一个可被更新的状态都要更新 
{
	tre[p].cl=tre[ls].cl;
	tre[p].cr=tre[rs].cr;
    tre[p].val=tre[ls].val+tre[rs].val;
    if(tre[ls].cr==tre[rs].cl) tre[p].val--;//判断 
}
void push_down(int p)
{
	tre[ls].cl=tre[ls].cr=tre[rs].cl=tre[rs].cr=tag[p];
	tre[ls].val=tre[rs].val=1;//贡献为0 
	tag[ls]=tag[rs]=tag[p];//区间覆盖取最新的懒标记直接覆盖前面的懒标记即可 
	tag[p]=0;//懒标记清零 
}
void build(int l,int r,int p)
{
	tre[p].l=l;
	tre[p].r=r;
	tre[p].mid=(l+r)>>1;
	if(l==r)
	{
		tre[p].val=1;
		tre[p].cl=tre[p].cr=wt[l];
		return;
	}
	build(l,tre[p].mid,ls);
	build(tre[p].mid+1,r,rs);
	push_up(p);
}
void modify(int p,int ql,int qr,int z)
{
	if(ql<=tre[p].l&&tre[p].r<=qr)
	{
		tag[p]=z;
		tre[p].cl=tre[p].cr=z;
		tre[p].val=1;
		return;
	}
	if(tag[p]) push_down(p);//注意tag标记别乱传，被清零再传就被0覆盖了，注意判断
	if(ql<=tre[p].mid) modify(ls,ql,qr,z);
	if(qr>tre[p].mid) modify(rs,ql,qr,z);
	push_up(p);
}
void query(int p,int ql,int qr)
{
	if(ql<=tre[p].l&&tre[p].r<=qr)
	{
		ans+=tre[p].val;
		if(tre[p].l==ql) L=tre[p].cl;//记录树链剖分中整个询问区间的左右端点颜色，方便第三个合并 
		if(tre[p].r==qr) R=tre[p].cr;
		return;
	}
	if(tag[p]) push_down(p);//注意 
	if(qr<=tre[p].mid) query(ls,ql,qr);//分三种情况讨论，方便合并 
	else if(ql>tre[p].mid) query(rs,ql,qr);
	else
	{
		query(ls,ql,qr);
		query(rs,ql,qr);
		if(tre[ls].cr==tre[rs].cl) ans--;//区间合并判断二 
	}
	
}
//---------------------------------------------- 

void dfs1(int u,int fat,int deep)
{
	dep[u]=deep;
	fa[u]=fat;
	siz[u]=1;
	int maxson=-1;//一定定义全局变量
	//或者直接这么写  if(siz[ev]>siz[mson[u]]) mson[u]=ev;因为一开始都是0所以没错 
	for(re int i=head[u];i;i=e[i].nxt)
	{
		int ev=e[i].v;
		if(ev==fat) continue;
		dfs1(ev,u,deep+1);
		siz[u]+=siz[ev];
		if(siz[ev]>maxson)
		{
			maxson=siz[ev];
			mson[u]=ev;
		}
	}
}
void dfs2(int u,int topf)
{
	id[u]=++cnt;
	top[u]=topf;
	wt[cnt]=w[u];
	if(!mson[u]) return;
	dfs2(mson[u],topf);
	for(int i=head[u];i;i=e[i].nxt)
	{
		int ev=e[i].v;
		if(ev==fa[u]) continue;
		if(ev==mson[u]) continue;
		dfs2(ev,ev);
	}
}
void add_Range(int u,int v,int k)
{
	while(top[u]!=top[v])
	{
		if(dep[top[u]]<dep[top[v]]) swap(u,v);
		modify(1,id[top[u]],id[u],k);
		u=fa[top[u]];
	}
	if(id[u]<id[v]) swap(u,v);
	modify(1,id[v],id[u],k);
}
int ask(int u,int v)
{
	int res=0,pos1=0,pos2=0;
	while(top[u]!=top[v])
	{
		if(dep[top[u]]<dep[top[v]]) swap(u,v),swap(pos1,pos2);//pos1,pos2千万别忘记交换 
		ans=0;
		query(1,id[top[u]],id[u]);
		res+=ans;
		if(R==pos1) res--; //右边界和上一次的左边界，第三个合并判断 
		pos1=L,u=fa[top[u]];//别忘了更新pos1 
	}
	if(dep[u]<dep[v]) swap(u,v),swap(pos1,pos2);
	ans=0; 
	query(1,id[v],id[u]);
	res+=ans;
	if(L==pos2) res--;
	if(R==pos1) res--;//最后注意两个边界可能都要更新，都要判断 
	return res; 
}
int main()
{
	n=read(),m=read();
	for(re int i=1;i<=n;++i) w[i]=read();
	for(re int i=1;i<n;++i)
	{
		x=read(),y=read();
		add(x,y);
		add(y,x);
	}
	dfs1(1,0,1);
	dfs2(1,1);
	build(1,n,1);
	for(re int i=1;i<=m;++i)
	{
		cin>>cs;
		if(cs=='C')
		{
			a=read(),b=read(),c=read();
			add_Range(a,b,c);
		}
		else if(cs=='Q')
		{
			a=read(),b=read();
			printf("%d\n",ask(a,b));
		}
	}
	return 0;
}