P10277 [USACO24OPEN] Bessie's Interview S 题解

P10277 [USACO24OPEN] Bessie's Interview S 题解

题目传送门

我的博客

思路

首先这道题第一问非常好做。只需要按照题目描述的那样模拟即可。即用优先队列存每个奶牛的面试时间，每次取出最小的时间，加入下一只奶牛。最后输出q.top()即可。伪代码如下。

for(i : from 1 to k){
    push a[i] into the queue
}
for(i : from k+1 to n){
    t = q.top()
    push a[i]+t into the queue
}
the answer is q.top()

再来看第二问。问哪些农夫可能会面试她。

显然，每个农夫会面试到哪只奶牛是不确定的，但是每只奶牛接受面试的时间是唯一确定的。所以我们可以先统计每只奶牛面试的开始时间和结束时间。当第 \(i\) 只奶牛的结束时间为 \(t\) 且第 \(j\) 只奶牛的开始时间也为 \(t\) 时，它们可能就能被同一个农夫面试。

想到了什么？笔者这里第一个想到的就是建图，然后跑dfs。具体怎么建图呢？我们发现，每次如果有 \(t\) 个农夫同时空闲下来，那么这 \(t\) 个农夫均有可能继续面试接下来 \(k\) 个奶牛。因此他们都需要和这些点连一条边。样例如下。

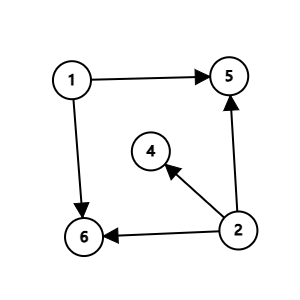
这时候只需要把上图反向一下，从 \(n\) 开始跑，看看那些再 \(1\) 到 \(k\) 内的点可以遍历到即可。

但是这样时间复杂度明显爆炸了。于是我们想，令状态 \(s\) 表示当前时间 \(time\) 接受采访可能会遇到的农夫有哪些。很容易发现对于奶牛 \(i\)，\(time+t_i\) 的状态和 \(time\) 的状态是一样的。于是可以让 \(time+t_i\) 向 \(time\) 连一条边。最后从 \(n\) 接受面试的时间开始遍历，统计有哪些 \(1\) 到 \(k\) 内可以到达的点。

因为 \(1 \leq t_i \leq 10^9\)，所以建图的时候很明显需要离散化。这里用map实现。

代码

const int N=3e5+10;
int n,k,cnt=0;
ll a[N],st[N],en[N];
ll ans1=0;//第一问答案
struct node{
	int id;
	ll w;
	bool operator < (const node &A)const {
		return w<A.w;
	}
};
priority_queue<node> q;//优先队列
struct edge{
	int nxt,to;
}e[N*10];
int head[N*10],num_Edge=0;
void add_Edge(int from,int to){
	e[++num_Edge].nxt=head[from];
	e[num_Edge].to=to;
	head[from]=num_Edge;
}
map<int,int> mp;//离散化用的map
int getid(int t){//查找离散化之后的下标
	if(mp.find(t)==mp.end()) mp[t]=++cnt;
    /*
    map.find函数返回的是一个迭代器，
    若查找成功，返回该键对应元素的迭代器；
    若未找到，返回与map.end()相同的迭代器
    */
	return mp[t];
}
int vis[N*10];//是否被遍历到
void dfs(int u){
	if(vis[u]) return ;
	vis[u]=1;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		dfs(v);
	}
}
signed main(){
	n=Read();k=Read();cnt=k;
	for(int i=1;i<=n;i++) a[i]=Read();
	for(int i=1;i<=k;i++){//1 到 k 直接进队
		st[i]=0ll,en[i]=a[i];
		q.push((node){i,-a[i]});//上面写的大根堆，查找最小值需要用小根堆，取反一下即可
		add_Edge(getid(en[i]),i);
	}
	for(int i=k+1;i<=n;i++){
		node t=q.top();q.pop();
		t.w=-t.w;
		st[i]=t.w;en[i]=t.w+a[i];
		q.push({i,-en[i]}); 
		add_Edge(getid(en[i]),getid(st[i]));//建反图
	}
	ans1=q.top().w;ans1=-ans1;
	printf("%lld\n",ans1);
	dfs(getid(ans1));//从 n 的面试时间开始遍历
	for(int i=1;i<=k;i++) printf("%d",vis[i]);
	return 0; 
}