P2416 泡芙 题解

P2416 泡芙 题解

题目传送门

我的博客

前言

笔者一开始写了一版 \(O(NQ)\) 的，竟然没有TLE？（但是WA了，且做法假了

本题做法：tarjan缩点+LCA。

思路

拿到这个题首先研究样例，发现样例中竟然有环。如下图。有环怎么办？

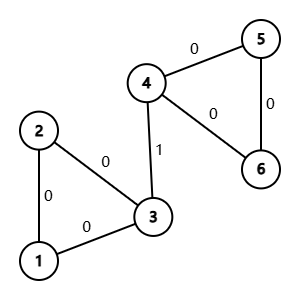
根据题意，我们可以得知，在一个环中的每一条边都可以走一遍。因此我们可以先把环缩成一个点，将环内的边权全部转化为缩点之后的点权。

缩点之后，剩下的边保证是一个树。此时我们不难想到，可以用倍增的思想，看一看路径上是否有边权为 \(1\) 的边（即是否有泡芙）。别忘记某一个点可能是一个环缩成的，所以也要考虑这个点的点权！

所以最终统计的就是

\[dis(u,lca(u,v))+dis(lca(u,v),v)+val_{lca(u,v)} \]

代码

const int N=3e5+10;
const int INF=0x3f3f3f3f;
int n,m,Q;
struct nodein{
	int x,y,z;
}in[N];//记录缩点之前的读入，方便建新图
struct edge{
	int nxt,to,w;
}e[N*10];//如果算不准开多大，空间足够的情况下尽可能开大一点
int head[N],num_Edge=0;
void add_Edge(int from,int to,int w){
	e[++num_Edge].nxt=head[from];
	e[num_Edge].to=to;
	e[num_Edge].w=w;
	head[from]=num_Edge;
}
//tarjan板子
int dfn[N],low[N],dfscnt=0;
int scc[N],sc=0,w[N];
int st[N],top=0;
void tarjan(int u,int fa){//这里的 fa 并不是父结点，而是读入时边的编号
//这里是改的时候懒得再改了，所以直接写了 fa。下文的 e[i].w 是懒得再开一个数组了。
	dfn[u]=low[u]=++dfscnt;
	st[++top]=u;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(fa==e[i].w) continue;//e[i].w 表示读入时边的编号。
		if(!dfn[v]){
			tarjan(v,e[i].w);
			low[u]=min(low[u],low[v]);
		}
		else {
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(dfn[u]==low[u]){
		sc++;
		while(st[top]!=u&&top){
			scc[st[top]]=sc;
			top--;
		}
		scc[st[top]]=sc;
		top--;		
	}
}
//以上------tarjan板子
//LCA板子
int ff[N][50],dep[N],sum[N];
void init_lca(){//初始化
	for(int j=1;j<=25;j++){
		for(int i=1;i<=n;i++){
			ff[i][j]=ff[ff[i][j-1]][j-1];
		}
	}
}
void dfs(int u,int fa){
	ff[u][0]=fa;
	dep[u]=dep[fa]+1;
	sum[u]+=w[u];//注意这里要累加点权
	for(int j=1;j<=25;j++){
		ff[u][j]=ff[ff[u][j-1]][j-1];
	}
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v==fa) continue;
		sum[v]=sum[u]+e[i].w;//更新之前累加点权！！！这里调了20分钟
		dfs(v,u);
	}
}
int lca(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=25;i>=0;i--){
		if(dep[ff[x][i]]>=dep[y]) x=ff[x][i];//注意可以取等！
	}
	if(x==y) return x;
	for(int i=25;i>=0;i--){
		if(ff[x][i]!=ff[y][i]){
			x=ff[x][i],y=ff[y][i];
		}
	}
	return ff[x][0];
} 
//以上LCA板子---------
signed main(){
	n=Read();m=Read();
	for(int i=1;i<=m;i++){
		int x=Read(),y=Read(),z=Read();
		add_Edge(x,y,i);//from,to,id
		add_Edge(y,x,i);
		in[i]=(nodein){x,y,z};
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]) tarjan(i,0);
	}
	for(int i=1;i<=n;i++) head[i]=0;//别忘了清空 head 数组！
	num_Edge=0;//这里为了缩减码量直接清空用了同一个数组
	for(int i=1;i<=m;i++){
		int u=scc[in[i].x],v=scc[in[i].y];
		if(u==v) w[u]+=in[i].z; //累加点权
		if(u!=v){//建新图
			add_Edge(u,v,in[i].z);
			add_Edge(v,u,in[i].z);
		}
	}
	init_lca();
	dfs(1,0);
	Q=Read();
	while(Q--){
		int x=Read(),y=Read();
		int fx=scc[x],fy=scc[y];
		if(fx==fy){//在一个环里，直接判断环内是否有边权为 1 的边
			if(w[fx]) puts("YES");
			else puts("NO");
		} 
		else {
			int f=lca(fx,fy);
			if(sum[fx]+sum[fy]-2*sum[f]+w[f]>0) puts("YES");
			else puts("NO");
		}
	}
	return 0; 
}