P5687 [CSP-S2019 江西] 网格图 题解

P5687 [CSP-S2019 江西] 网格图 题解

题目传送门

我的博客

前言

这道题没有什么特别高深的算法，就是一个贪心。

个人认为难点在于题目没有给出相应的图（自己画，很简单）。画出图来之后结合样例解释基本上就做出来了。

思路

拿到这个题，乍一看，感觉有点摸不着头脑。对于 \(n,m \leq 3 \times 10^5\)，显然不可以暴力建边求最小生成树。

怎么办呢？我们先从样例研究入手。如下图。

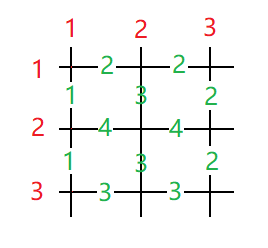
结合样例解释，我们发现：最终选取的是第一行的 \(2\) 和第一列、第二列、第三列的 \(1,3,2\)。

于是我们不难发现，肯定要把边从小到大排序一下，每次取最小的边。但是不完全是这样的。\(n\) 个结点的最小生成树最多有 \(n-1\) 条边，同理，\(n \times m\) 的最小生成树最多有 \(n \times m -1\) 条边，且在本题中不能构成环。

于是我们可以把行和列分开来看。

先考虑行（列同理，不再赘述）：每一行上至多有 \(n-1\) 条边。

那是不是所有的行都要连 \(n-1\) 条边？

显然不是，这样就构成了环。所以我们需要去掉一些边，保证最小生成树上不存在环。

如何求出可以去掉的边？

假设我们已经连了 \(r\) 行 \(c\) 列。首先我们按照上面步骤把 \(n-1\) 条边全部连上。如果出现环，那么可以去掉 \(c-1\) 条边。

怎样判断出现环？

我们发现，当 \(r==1\) 或者 \(c==1\) 的时候不会出现环，随着 \(r,c\) 的增加，一定会有环出现。（请读者自行画图）

于是，我们整体的代码思路就出来了。

总结

1. 对所有权值从小到大排序。
2. 行和列分别处理，统计答案。
3. 当连边足够时，break。

时间复杂度瓶颈在于排序，为 \(O((n+m) \log (n+m))\)。

易错点

• 不要担心 MLE ，数组尽量开大一点。
• 判断 break 的时候一定想清楚。
• 排序的时候写清楚 \(<\) 还是 \(>\)。

代码

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define int long long //十年 OI 一场空，不开_______见祖宗
#define ___ __int128
#define INF 0x3f3f3f3f3f3f3f3f 
inline int Read(){
    int x=0,f=1;
    char c=getchar();
    while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-48;c=getchar();}
    return x*f;
}
inline void Write(int x){
	if(x<0) {putchar('-');x=-x;}
	if(x>9) Write(x/10);
	putchar(x%10+'0');
}
const int N=3e5+10;//注意看数据范围，不是 1e5
int n,m,tot=0;
int r,c,ans=0;
//r: 统计已经连了多少行
//c: 统计已经连了多少列
struct node{
	int v,op;
}a[N*10];
bool cmp(node A,node B){return A.v<B.v;}
signed main(){
	n=Read();m=Read();
	for(int i=1;i<=n;i++) {
		a[++tot].v=Read();a[tot].op=1;//记录是行(1)还是列(2)
	}
	for(int i=1;i<=m;i++){
		a[++tot].v=Read();a[tot].op=2;
	}
	sort(a+1,a+tot+1,cmp);//排序
	for(int i=1;i<=tot;i++){
		if(a[i].op==1){
			r++;
			if(r<=1||c<=1) ans+=(m-1)*a[i].v;//连的第一行，此时没有环，不需要删边
			else ans+=(m-c)*a[i].v;
		}
		else{
			
			c++;
			if(r<=1||c<=1) ans+=(n-1)*a[i].v;////连的第一列，此时没有环，不需要删边
			else ans+=(n-r)*a[i].v;
		}
		if(r>=n&&c>=m) break;//如果边数够了，结束循环。
	}
	printf("%lld\n",ans);
	return 0; 
}