P2650 弹幕考察 题解

P2650 弹幕考察 题解

题目链接

本人博客

前言

做法1：树状数组

做法2：二分

以上两个做法在本篇题解中均会涉及。

笔者一拿到这个题，就想到了用数据结构维护一个查询区间内原区间的个数。再一看是明显是离线查询，故想到了树状数组。打完之后点开标签，发现竟然有二分的标签，于是看了题解，才恍然大悟，发现原来这个题原来可以这么简单？！

有些人啊，就是学数据结构学傻了。
连差分都要用线段树做。
—— XXXXXXX

做法1：树状数组

从后往前维护树状数组，统计答案。

注意到数据，发现没有办法维护如此之巨大的树状数组，怎么办？

答案就是-离散化！

\(\color{red}{\text{注意：离散化后数组大小一定想好要开多大！}}\) 笔者就是这里被卡了 \(5\) 发。

代码

#include<cstdio>
#include<iostream> 
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
#define int long long 
inline int Read(){
	int x=0,f=1;
	char c=getchar();
	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
	while(isdigit(c)){x=x*10+c-48;c=getchar();}
	return x*f;
}
inline void Write(int x){
	if(x<0){x=-x;putchar('-');}
	if(x>9) Write(x/10);
	putchar(x%10+'0');
}
const int N=1e6+10;
int n,m,rr;
//rr：统计离散化后最右边的数字
int li[N],totl=0;
int ans[N];
struct node{
	int l,r,id;
}a[N],q[N]; 
//a:原区间,q:查询区间
bool cmp1(node A,node B){return A.r>B.r;}
bool cmp2(node A,node B){return A.l>B.l;}
//树状数组板子
int c[N*5];
int lowbit(int x){
	return x&(-x);
}
void change(int pos,int v){
	while(pos<=rr){
		c[pos]+=v;
		pos+=lowbit(pos);
	}
}
int query(int pos){
	int res=0;
	while(pos){
		res+=c[pos];
		pos-=lowbit(pos);
	}
	return res;
}
signed main(){
	n=Read();m=Read();
	for(int i=1;i<=n;i++){
		a[i].l=Read()+1,a[i].r=Read()+a[i].l;
		li[++totl]=a[i].l,li[++totl]=a[i].r;
	}
	for(int i=1;i<=m;i++){
		q[i].l=Read()+1,q[i].r=Read()+q[i].l;
		li[++totl]=q[i].l,li[++totl]=q[i].r;
		q[i].id=i;
	}
        //离散化
	sort(li+1,li+totl+1);
	int cnt=unique(li+1,li+totl+1)-(li+1);
	for(int i=1;i<=n;i++) {
		a[i].l=lower_bound(li+1,li+cnt+1,a[i].l)-li;
		a[i].r=lower_bound(li+1,li+cnt+1,a[i].r)-li;
		rr=max(rr,a[i].r);
	}
	for(int i=1;i<=m;i++){
		q[i].l=lower_bound(li+1,li+cnt+1,q[i].l)-li;
		q[i].r=lower_bound(li+1,li+cnt+1,q[i].r)-li;
		rr=max(rr,q[i].r);
	}
	sort(a+1,a+n+1,cmp1);
	sort(q+1,q+m+1,cmp2);
	int j=1;
	for(int i=1;i<=m;i++){
		while(a[j].r>q[i].l) {
			change(a[j].l,1);
			j++;
		}
		ans[q[i].id]=query(q[i].r-1);
	}
	for(int i=1;i<=m;i++) printf("%lld\n",ans[i]);
	return 0; 
}

做法2：二分

考虑什么时候原区间对查询区间有贡献。

设原区间为 \([x,y]\)，查询区间为 \([l,r]\)。

当 \(y < l\) 或者 \(x > r\) 的时候原区间不在查询区间的覆盖范围内，此时无贡献。如下图。

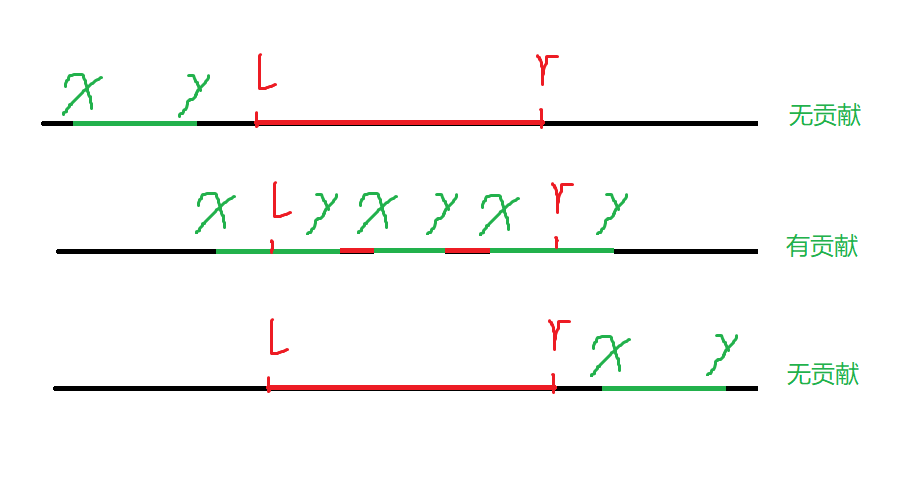
所以只需要统计查询区间右端点前原区间左端点的个数，减去查询区间左端点前原区间右端点的个数。

代码

#include<cstdio>
#include<iostream> 
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
#define int long long 
inline int Read(){
	int x=0,f=1;
	char c=getchar();
	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
	while(isdigit(c)){x=x*10+c-48;c=getchar();}
	return x*f;
}
inline void Write(int x){
	if(x<0){x=-x;putchar('-');}
	if(x>9) Write(x/10);
	putchar(x%10+'0');
}
const int N=1e5+10;
int n,m,l[N],r[N];
signed main(){
	n=Read();m=Read();
	for(int i=1;i<=n;i++){
		l[i]=Read(),r[i]=Read()+l[i]-1;//注意这里是左闭右开
	}
	sort(l+1,l+n+1);
	sort(r+1,r+n+1);//二分需要满足单调性
	for(int i=1;i<=m;i++){
		int x=Read(),y=Read()+x;
		int ans=lower_bound(l+1,l+n+1,y)-(l+1);
		ans-=lower_bound(r+1,r+n+1,x)-(r+1);
		printf("%lld\n",ans);
	}
	return 0; 
}