基于RSA的实用门限签名算法

摘自：https://zhuanlan.zhihu.com/p/135258941

1 门限签名

门限签名是普通数字签名的一个重要分支，是门限秘密共享技术和数字签名的一种结合。1991年，Desmedt-Frankel首次提出了 $(t,n)$ 门限签名方案。 $(t,n)$ 门限签名方案是指由 $n$ 个成员组成一个签名群体，该群体有一对公钥和私钥，群体内大于等于 $t$ 个合法、诚实的成员组合可以代表群体用群私钥进行签名，任何人可利用该群体的公钥进行签名验证。这里 $t$ 是门限值，只有大于等于 $t$ 个合法成员才能代表群体进行签名，群体中任何 $t-1$ 个或更少的成员不能代表该群体进行签名，同时任何成员不能假冒其他成员进行签名。采用门限签名方式可以实现权力分配，避免滥用职权。

2 基于RSA的门限签名

本算法[1]由IBM实验室提出，算法有以下特点：

1. it is unforgeable and robust in the random oracle model, assuming the RSA problem is hard;
2. signature share generation and verification is completely non-inter-active;
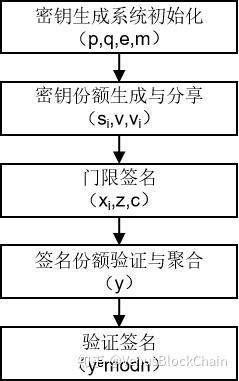
3. the size of an individual signature share is bounded by a constant times the size of the RSA modulus.

算法流程：

2.1 RSA算法

2.1.1 RSA加解密

首先，RSA算法的安全性是建立在大整数因子分解的困难性之上的。

秘钥生成：选择两个互异的大素数 $p$ 和 $q$ ，二者保密。计算 $n=pq$ ，公开 $n$ 。 $\phi(n) = (p-1)(q-1)$ ， $\phi(n)$ 保密，选择一个公开的随机数 $e(0< e < \phi(n))$ ，满足 $gcd(e, \phi(n))=1$ ，计算 $d=e^{-1}mod \phi(n)$ ， $d$ 保密。此时，公钥为 $(e,n)$ ，私钥为 $(d,n)或(d,p,q)$ 。
加密：加密结果 $C=M^emodn$ ，已知条件 $M < n$ ，公钥 $(e,n)$ 。
解密：解密结果 $M=C^dmodn$ ，已知条件 $C$ ，私钥 $(d,n)$ 。

2.1.2 RSA签名验签

选取整数 $n=pq$ ，消息空间与签名空间均为整数空间，即 $M=A=Z_n$ ，定义秘钥集合 $K=\{ (n,e),(p,q,d)|n=pd,d\times e \equiv 1mod \phi(n)\}$ 。

对 $x \in M$ ，Bob要对 $x$ 签名，取 $k \in K$ ， $sig_k(x)=x^dmodn=y$ ，于是验证等式 $x=y^emodn$ 是否成立。

2.2 系统初始化

系统中有 $l$ 个参与者，编号分别为 $1,...,l$ ，有一个可信的dealer和一个敌手adversary。dealer选择两个长度（512bit）相等的素数 $p$ 和 $q$ ，设 $p=2p'+1，q=2q'+1$ ，其中 $p',q'$ 也都是素数。RSA模 $n=pq$ ，令 $m=p'q'$ ，并选择公共一个素数指数 $e，e>l$ 。

此时，RSA公钥为 $PK=(n,e)$ 。

2.3 密钥分享

接下来，dealer选择 $d，d \in Z$ ，满足 $de\equiv 1modm$ ，即 $d$ 就是要分享的秘密值。设置 $a_0=d$ ，dealer随机的选择 $a_i，a_i \in {0,...,m-1}，1 \leq i \leq k-1，k$ 为门限值。即构成的关于 $k-1$ 次多项式为 $f(X)=\sum_{i=0}^{k-1}{a_iX^i}$ 。

对于 $1 \leq i \leq l$ ，计算分享的密钥值 $s_i：s_i=f(i)modm$ 。 $s_i$ 就是对于参与者 $i$ 的私钥 $SK_i$ 。

接下来，计算 verification keys，用于验证签名的是否有效。dealer选择一个随机值 $v \in Q_n$ ，并计算 $v_i = v^{s_i} \in Q_n，1 \leq i \leq l$ ，令 $VK=v,VK_i=v_i$ 。

接下来，计算拉格朗日系数。令 $\delta = l!$ ，对于集合大小为 $k$ 的子集 $S$ ，其中元素均属于 ${0,...,l}$ ，对于任何 $i \in {0,...,l \backslash S},j \in S$ ，定义:

$\lambda_{i,j}^S=\delta \frac{\prod_{j' \in {S \backslash{j}}}(i-j')} {\prod_{j' \in {S \backslash{j}}}(j-j')} \\$

这些值是标准拉格朗日插值公式系数。从拉格朗日插值公式可得：

$\delta \cdot f(i) \equiv \sum_{j \in S} \lambda_{i,j}^S f(j)modm \\$

2.4 生成门限签名份额

下面，计算一个关于消息 $M$ 的一个签名份额：令 $x=H(M)$ ，对于参与者 $i$ 计算 $x_i=x^{2\delta s_i} \in Q_n$ ， $x_i$ 是一个参与者 $i$ 的签名份额。

每个签名份额对于有一个正确性的证明，这个正确性证明仅对于基 $\tilde{x}=x^{4\delta}$ 的 $x^2$ 离散对数与对于基 $v$ 的 $v_i$ 离散对数相似。

下面，计算内阁签名份额的正确性证明以及如何验证这个签名份额： $L(n)$ 是 $n$ 的比特长度， $H'$ 是一个hash函数，函数输出一个 $L_1$ bit的整数，此处 $L_1 = 128$ 是第二个安全参数。为了生成正确性证明，参与者选择随机数 $r \in \{ 0,...,2^{L(n)+2L_1} -1 \}$ ，计算：

$v'=v^r,x'=\tilde{x}^r,c=H'(v,\tilde{x},v_i,x_i^2,v',x'),z=s_i+r \\$

此时，正确性证明就变成 $(z,c)$ 。为了验证这个证明，只需要检查下面等式是否成立：

$c=H'(v,\tilde{x},v_i,x_i^2,v^zv_i^{-c},\tilde{x}^zx_i^{-2c}) \\$

此处，计算的是 $x_i^2$ ，而不是 $x_i$ ，原作者是这样解释的：Although $x_i$ is supposed to be a square, this is not easily verified. This way, we are sure to be working in $Q_n$ , where we need to be working to ensure soundness.

2.5 组合签名份额

在组合所有签名份额之前，先要验证每一个签名份额，并且要满足有效的签名份额个数不能小于门限 $k$ 。

假设此处有一组有效的签名份额集合 $S$ ， $S=\{i_1,...i_k\} \subset \{1,...,l\}$ 。令 $x=H(M) \in Z_n^\ast$ ，且假设 $x_{i_j}^2=x^{4 \delta s_{i_j}}$ 。然后组合签名份额，计算：

$w=x_{i_1}^{2 \lambda_{0,i_1}^S} ... x_{i_k}^{2 \lambda_{0,i_k}^S} \\$

此处的 $\lambda$ 就是2.3节中的 $\lambda_{i,j}^S$ 。根据 $\delta \cdot f(i) \equiv \sum_{j \in S} \lambda_{i,j}^S f(j)modm$ ，可得 $w^e=x^{e'}$ ，此处 ${e'=4 \delta^2}$ 。