补题:2020牛客暑期多校训练营(第二场)
Solved:7/11
Upsolved:11/11
A. All with Pairs (牛客 5667A)
首先,所有前缀/后缀的总数为$\sum |s_i|$级别的,所以不妨把所有后缀出现的个数先hash后用unordered_map统计一遍。
此时对于每个串的前缀,若与某些后缀相等,那么就能产生 后缀出现次数$\times$前缀长度的平方 的贡献。不过这样会产生重复:如果一个前缀为abcab,且有一定数量与之相等的后缀,那么一定存在不少于这个数目的、等于ab的后缀(毕竟ab就是abcab的后缀)。但是在我们的统计中,在abcab中会计算一次贡献,在ab中又会计算一次贡献,而后者是我们不希望看到的。
能够发现,所有会产生多余贡献的前缀,一定是一个更长的前缀在KMP中的nxt。于是考虑对每个字符串$s_i$求一次nxt数组,对于第$i$位($i$从$0$到$n-1$),能够产生$cnt[s_1...s_i]\cdot (i+1)^2$的贡献,并且如果$nxt[i]\neq -1$,就需要减去$cnt[s_1...s_i]\cdot (nxt[i]+1)^2$的重复贡献。简单验证能够发现这样确实能将重复贡献全部去除。
用unsigned long long自然溢出来hash真香。

#include <cstring> #include <iostream> #include <algorithm> #include <unordered_map> using namespace std; typedef unsigned long long ull; const int N=1000005; const int mod=998244353; int n; string s[N]; ull h[N]; int fail[N]; unordered_map<ull,int> cnt; int main() { ios::sync_with_stdio(false); cin>>n; for(int i=1;i<=n;i++) { cin>>s[i]; ull tmp=0,base=1; for(int j=s[i].length()-1;j>=0;j--) { tmp=tmp+(s[i][j]-'a'+1)*base; ++cnt[tmp]; base=base*2333; } } long long ans=0; for(int i=1;i<=n;i++) { int p=-1; fail[0]=-1; for(int j=1;j<s[i].length();j++) { while(p!=-1 && s[i][p+1]!=s[i][j]) p=fail[p]; if(s[i][p+1]==s[i][j]) ++p; fail[j]=p; } ull tmp=0; for(int j=0;j<s[i].length();j++) h[j]=tmp=tmp*2333+s[i][j]-'a'+1; for(int j=s[i].length()-1;j>=0;j--) { ans=(ans+1LL*cnt[h[j]]*(j+1)%mod*(j+1))%mod; if(fail[j]!=-1) ans=(ans-1LL*cnt[h[j]]*(fail[j]+1)%mod*(fail[j]+1)%mod+mod)%mod; } } cout<<ans<<'\n'; return 0; }
B. Boundary (牛客 5667B)
rls用圆反演做的,变成了过原点直线通过的点数。
不过题解中的做法也很方便,利用了同一弦的圆周角相同的性质。先枚举一个点$i$,与原点相连就可以得到一条弦;再枚举一个点,看弦的圆周角的众数是多少即可。为了避免将弦两侧的圆周角都统计进去,可以考虑使用向量叉积、要求叉积必须小于/大于$0$。那么圆周角可以用点积除以叉积表示,即$\frac{1}{tan\theta}$。
写的时候用了分数类。不过这题中只有一次除法,用浮点也应该无所谓。

#include <map> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; struct Point { int x,y; Point(int a=0,int b=0) { x=a,y=b; } }; inline Point operator -(const Point &X,const Point &Y) { return Point(X.x-Y.x,X.y-Y.y); } struct frac { ll x,y; frac(ll a=0,ll b=1) { ll gcd=__gcd(a,b); x=a/gcd,y=b/gcd; } }; inline bool operator <(const frac &X,const frac &Y) { return X.x*Y.y<Y.x*X.y; } const int N=2005; inline int mul(const Point &X,const Point &Y) { return X.x*Y.x+X.y*Y.y; } inline int cross(const Point &X,const Point &Y) { return X.x*Y.y-X.y*Y.x; } int n; Point p[N]; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d%d",&p[i].x,&p[i].y); int ans=0; for(int i=1;i<=n;i++) { int mx=0; map<frac,int> mp; for(int j=1;j<=n;j++) { int val=cross(p[j],p[j]-p[i]); if(val<=0) continue; frac res(mul(p[j],p[j]-p[i]),cross(p[j],p[j]-p[i])); mx=max(++mp[res],mx); } ans=max(ans,mx+1); } printf("%d\n",ans); return 0; }
C. Cover the Tree (牛客 5667C)
这题有很多乱搞的策略。首先可以目测出来,答案为总叶子数除以二。
在现场我们的做法是,先用类似找树的重心的方法找出树上的一个节点,使得其所有儿子的子树内最大的叶子数最小。然后将叶子数最大的子树拿出来,此时其叶子数$maxl$一定不超过总数的$\frac{1}{2}$。在其余子树的叶子中留出$maxl$个,然后将其他的叶子与不在同一子树内的进行两两配对(这样的方案一定存在,因为剩余子树中最大叶子数也不超过$maxl$),留出的$maxl$个与最大子树内的进行配对。如果最后还留下一个(总叶子数可能为奇数),就与根相连即可。

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef pair<int,int> pii; const int N=200005; int n; vector<int> v[N]; int root; int sz[N],mx[N]; inline void find(int x,int fa,int tot) { if((int)v[x].size()==1) sz[x]=1; mx[x]=0; for(int i=0;i<v[x].size();i++) { int nxt=v[x][i]; if(nxt==fa) continue; find(nxt,x,tot); sz[x]+=sz[nxt]; mx[x]=max(mx[x],sz[nxt]); } mx[x]=max(mx[x],tot-sz[x]); if(!root || mx[x]<mx[root]) root=x; } vector<int> pool[N]; void dfs(int x,int f,int id) { if((int)v[x].size()==1) pool[id].push_back(x); for(int i=0;i<v[x].size();i++) { int y=v[x][i]; if(y!=f) dfs(y,x,id); } } pii ord[N]; int main() { scanf("%d",&n); for(int i=1;i<n;i++) { int x,y; scanf("%d%d",&x,&y); v[x].push_back(y); v[y].push_back(x); } int leaf=0; for(int i=1;i<=n;i++) if((int)v[i].size()==1) leaf++; printf("%d\n",(leaf+1)/2); find(1,0,leaf); int m=(int)v[root].size(); for(int i=0;i<m;i++) dfs(v[root][i],root,i),ord[i]=pii((int)pool[i].size(),i); sort(ord,ord+m); vector<pii> ans; int l=0,r=m-2,maxl=ord[m-1].first; while((leaf-maxl)>maxl) { ans.push_back(pii(pool[ord[l].second].back(),pool[ord[r].second].back())); pool[ord[l].second].pop_back(); pool[ord[r].second].pop_back(); if((int)pool[ord[l].second].size()==0) l++; if((int)pool[ord[r].second].size()==0) r--; leaf-=2; } while(l<=r) { ans.push_back(pii(pool[ord[l].second].back(),pool[ord[m-1].second].back())); pool[ord[l].second].pop_back(); pool[ord[m-1].second].pop_back(); if((int)pool[ord[l].second].size()==0) l++; } if((int)pool[ord[m-1].second].size()>0) ans.push_back(pii(root,pool[ord[m-1].second][0])); for(int i=0;i<ans.size();i++) printf("%d %d\n",ans[i].first,ans[i].second); return 0; }
D. Duration (牛客 5667D)
签到。

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; int main() { int h,m,s; scanf("%d:%d:%d",&h,&m,&s); ll t1=h*3600+m*60+s; scanf("%d:%d:%d",&h,&m,&s); ll t2=h*3600+m*60+s; printf("%lld\n",abs(t2-t1)); return 0; }
E. Exclusive OR (牛客 5667E)
看到xor的题目,第一反应是线性基。由于$A_i<2^{18}$,故线性基的秩也不超过$18$,也就是说如果我们选择了不少于$18$个数,一定能取到最大值。
不过对于$i<18$的答案并没有办法用线性基求解。直到rls提了一句FWT才发现已经快忘了有这个东西了...直接把所有数用FWT卷起来就行了,卷$i$次就相当于选了$i$个数,IFWT以后看哪一位不为$0$就说明这个数能被选出来。为了防止溢出,可以在卷一次以后将所有大于$0$的数全部改成$1$。
不过这样交上去以后WA了。要考虑一些特殊情况:假如$A_i$均为$1$,那么选奇数个时必为$1$,选偶数个时必为$0$。这说明答案还和奇偶性相关,所以需要FWT一直卷到$i=20$,之后的答案就按照奇偶性等于$i=19,i=20$的了。

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=200005; void FWTxor(ll *a,int n) { for(int i=n;i>=2;i>>=1) { int m=i>>1; for(int j=0;j<n;j+=i) for(int k=0;k<m;k++) { ll x=a[j+k],y=a[j+m+k]; a[j+k]=x+y; a[j+m+k]=x-y; } } } void IFWTxor(ll *a,int n) { for(int i=n;i>=2;i>>=1) { int m=i>>1; for(int j=0;j<n;j+=i) for(int k=0;k<m;k++) { ll x=a[j+k],y=a[j+m+k]; a[j+k]=(x+y)/2; a[j+m+k]=(x-y)/2; } } } int n; int a[N],ans[N]; ll b[1<<19],tmp[1<<19]; int main() { scanf("%d",&n); int mx=0; for(int i=1;i<=n;i++) scanf("%d",&a[i]),b[a[i]]=1,mx=max(mx,a[i]); int m=1; while(m<=mx) m<<=1; tmp[0]=1; FWTxor(b,m); FWTxor(tmp,m); for(int i=1;i<=min(n,20);i++) { for(int j=0;j<m;j++) tmp[j]=tmp[j]*b[j]; IFWTxor(tmp,m); for(int j=m-1;j>=0;j--) if(tmp[j]>0) { tmp[j]=1; ans[i]=max(ans[i],j); } FWTxor(tmp,m); printf("%d ",ans[i]); } for(int i=21;i<=n;i++) printf("%d ",ans[20-i%2]); return 0; }
F. Fake Maxpooling (牛客 5667F)
其实对$nm$个数求gcd还挺危险的,不过现场貌似正好能过。倒是卡了空间,所以需要将一个数组复用。
题解给的做法是,用类似埃氏筛的方法,找到互质的两个数,然后成倍增长。由于每对数只会被选到一次,所以是$O(nm)$的。
接着就是每个$k\times k$矩阵中的最大值了,可以用两次单调队列处理。第一次,求出每一行中,每$k$个数中的最大值;第二次,求出每一列中,之前求出的行中最大值的最大值。维护一个单调队列,其中存的是下标,越靠队头数越小、越靠队尾数越大,这样就可以方便地在队尾到当前位置大于$k$时弹出队尾了。

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=5005; int n,m,sz; int gcd[N][N],a[N][N]; int head,rear,q[N]; int main() { scanf("%d%d%d",&n,&m,&sz); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(!gcd[i][j]) for(int k=1;k*i<=n && k*j<=m;k++) gcd[i*k][j*k]=k,a[i*k][j*k]=i*j*k; for(int i=1;i<=n;i++) { head=1,rear=0; for(int j=1;j<=m;j++) { while(head<=rear && a[i][j]>=a[i][q[rear]]) rear--; q[++rear]=j; gcd[i][j]=a[i][q[head]]; if(j>=sz && j-sz+1==q[head]) head++; } } ll ans=0; for(int i=sz;i<=m;i++) { head=1,rear=0; for(int j=1;j<=n;j++) { while(head<=rear && gcd[j][i]>=gcd[q[rear]][i]) rear--; q[++rear]=j; if(j>=sz) { ans+=gcd[q[head]][i]; if(j-sz+1==q[head]) head++; } } } printf("%lld\n",ans); return 0; }
G. Greater and Greater (牛客 5667G)
这题涉及到的是一个Shift And的思想,之后还得好好学一学。
具体的做法是这样的:首先可以对于$a$数组中的每一个元素求一个bitset $s$,其中$s_i[j],1\leq j\leq m$表示$a[i]$是否大于$b[j]$(即将$a[i]$与$b$数组整个比一遍)。这样看似需要求$n$个bitset,但是实际上只有$m$级别的不同的bitset,因为一个数只可能比$b$中的$0,1,...,m$个数大。所以只需要对$b$求$m$个bitset,$a[i]$对应的bitset在排序后的$b$数组中二分即可。
接着考虑用bitset $cur[i]$表示$a$中子段$a[i...i+m-1]$与$b$的大小关系。其中$cur[i][j]$表示,是否有$\forall k\in [j,m],a[i+(k-j)]\geq b[k]$($i$向右长度为$m-j+1$的子段是否依次大于等于$b$中的等长后缀),也就是说$i-j+1$是否为一个合法的起点(仅考虑$a[i...m-j+1]$时)。知道这个的用处在于,我们可以向后推一位。假如$a[i-1]\geq b[j-1]$,那么我们就知道了$i-1$向右长度为$m-j+2$的子段也依次大于等于$b$中的等长后缀,即$cur[i-1][j-1]=1$。
于是$cur$可以这样转移:$cur[i]=((cur[i+1]\text{>>}1) | (1\text{<<}m)) \text{&} s[i]$,若$cur[i][1]=1$那么就会对答案有$1$的贡献。这样理解会直观一点:$s[i]$表示$a[i]$能大于等于$b$中哪些位,于是就能排除掉一些起点$j\leq i$。同时$cur[i+1]$中已经排除了一些起点$j$,所以两者的and就是当前可能的起点。
也有更省空间的做法,不用存下$m$个bitset,而是将$a,b$排序后一起处理。

#include <cstdio> #include <bitset> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef pair<int,int> pii; const int N=150005; const int M=40005; int n,m; int a[N],b[M]; vector<pii> v; int pos[N]; bitset<M> s[M]; int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=m;i++) scanf("%d",&b[i]),v.push_back(pii(b[i],i)); v.push_back(pii(0,0)); sort(v.begin(),v.end()); for(int i=1;i<v.size();) { s[i]=s[i-1]; int j=i; while(j<v.size() && v[j].first==v[i].first) { s[i].set(v[j].second); j++; } for(int k=i+1;k<j;k++) s[k]=s[i]; i=j; } for(int i=1;i<=n;i++) { int p=lower_bound(v.begin(),v.end(),pii(a[i],0))-v.begin(); if(p==v.size() || v[p].first>a[i]) p--; pos[i]=p; } int ans=0; bitset<M> cur,Im; Im.set(m); for(int i=n;i>=1;i--) { cur=((cur>>1)|Im)&s[pos[i]]; if(cur.test(1)) ans++; } printf("%d\n",ans); return 0; }
H. Happy Triangle (牛客 5667H)
集合$MS$中的数$a,b$(不妨认为$a\leq b$)能与$x$构成三角形仅有以下几种情况:
1. $a\leq b\leq x$,此时若有$a+b>x$即可。
2. $a\leq x\leq b$,此时若有$a+x>b$即可。
3. $x\leq a\leq b$,此时若有$a+x>b$即可。
2、3的条件虽然相同,但是由于$a,b,x$之间的大小关系不同,仍需要分开处理。1很简单,从$MS$中取出两个小于$x$、且最接近$x$的数。2也差不多,从$MS$中取出一个大于$x$、一个小于$x$的最接近$x$的数。3判断起来就比较麻烦了,需要找出最小的$b-a$,且满足$a\geq x$。
这其实可以通过离散化+线段树来维护。显然最小的$b-a$一定产生在相邻两数之间,所以我们需要维护的是相邻两数之差的最小值(这个差被放在较小数的位置上)。这样查询的时候$query(x,sz)$即可,稍微麻烦点的是插入、删除。往$a,b$中插入一个$x$时,本来在$a$处的$b-a$被抹去了,而变成了$a$处的$x-a$和$x$处的$b-x$。而删除$a,x,b$中的$x$时,本来在$a$处的$x-a$、在$x$处的$b-x$被抹去了,而变成了$a$处的$b-a$。不过需要注意出现重复数字时的判断,如果$a$有重复,那么在插入时$a$的值为$0$不变,在删除时有可能从$0$变成$b-a$,用multiset中的count函数判断一下就好了。
一个小技巧,就是可以在multiset中预先插入$-1$和$\infty$,相当于给定了左边界和右边界,可以省去不少繁琐的讨论。

#include <set> #include <vector> #include <cstdio> #include <algorithm> using namespace std; const int N=200005; const int INF=1<<30; int sz=1,t[N<<2]; inline void modify(int k,int x) { k=k+sz-1; t[k]=x; k>>=1; while(k) { t[k]=min(t[k<<1],t[k<<1|1]); k>>=1; } } inline int query(int k,int l,int r,int a,int b) { if(a>r || b<l) return INF; if(a>=l && b<=r) return t[k]; int mid=(a+b)>>1; return min(query(k<<1,l,r,a,mid),query(k<<1|1,l,r,mid+1,b)); } int n; int opt[N],val[N]; multiset<int> s; vector<int> v; inline int pos(int x) { return lower_bound(v.begin(),v.end(),x)-v.begin()+1; } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d%d",&opt[i],&val[i]),v.push_back(val[i]); while(sz<n) sz<<=1; for(int i=1;i<(sz<<1);i++) t[i]=INF; sort(v.begin(),v.end()); v.resize(unique(v.begin(),v.end())-v.begin()); s.insert(-1),s.insert(INF); for(int i=1;i<=n;i++) { int prev=*(--s.lower_bound(val[i])); int next=*(s.lower_bound(val[i])); if(opt[i]==1) { s.insert(val[i]); if(prev!=-1 && s.count(prev)==1) modify(pos(prev),val[i]-prev); if(next!=INF) modify(pos(val[i]),next-val[i]); } if(opt[i]==2) { s.erase(s.lower_bound(val[i])); next=*s.upper_bound(val[i]); if(s.count(val[i])==0) { modify(pos(val[i]),INF); if(prev!=-1 && s.count(prev)==1) modify(pos(prev),next==INF?INF:next-prev); } if(s.count(val[i])==1) modify(pos(val[i]),next==INF?INF:next-val[i]); } if(opt[i]==3) { int flag=0; if(prev!=-1) { int pprev=*(--(--s.lower_bound(val[i]))); if(pprev!=-1 && prev+pprev>val[i]) flag=1; } if(prev!=-1 && next!=INF && prev+val[i]>next) flag=2; if(query(1,pos(val[i]),sz,1,sz)<val[i]) flag=3; printf(flag?"Yes\n":"No\n"); } } return 0; }
I. Interval (牛客 5667I)
将这个问题向网格图上转化是很自然的思路。原题目中的区间$[l,r]$就相当于网格上的$(l,r)$,原题目中$\{l,r,L\}$的限制就相当于$(l,r)$和$(l+1,r)$间的边不能走,$\{l,r,R\}$的限制同理。
之后需要有网络流的直觉(我又没有...)。这题可以转化成一个最大流模型:源点是$(1,n)$,汇点自己建,如果两点之间有$\{l,r,L/R,c\}$的限制则流量为$c$,否则流量为$\infty$,所有$(i,i)$都向汇点连流量为$\infty$的边。此时的最大流就是题目中的答案。为什么最大流求出的会是题目中的“最小代价”呢?因为假设$(1,n)$外的限制有很多层,每一层的代价之和互不相同,那么从$(1,n)$流到$(i,i)$的最大流量,取决于代价之和最小(即总流量最小)的那一层。
不过这样还不算完。当前的图是$n^2$点$n^2$边的,直接跑Dinic肯定吃不消,还需要进行一个奇妙的转化。
可以参考:MaxMercer - 对偶图对于平面图最小割的求解(网络流问题),得到的结论是平面图的最小割等于对偶图的最短路。本题中的网格图显然是平面图,那么考虑怎么构造对偶图。
首先将源点与汇点连一条线(图中蓝线),这条线所新围成的面对应的对偶图中点为$S'$,最外面的面对应的对偶图中点为$T'$。对偶图中$S'$到$T'$的边长度为$0$(相当于在原图中添加一条$S$到$T$流量为$0$的边,这并不会改变最小割),其余的边等于穿过的原图中边的长度。
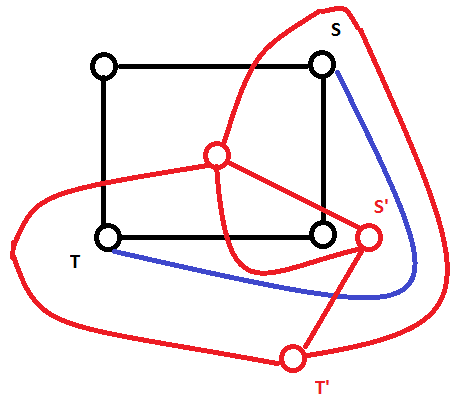
不过上面的图比较特殊,实际上原图大概长下图这样:
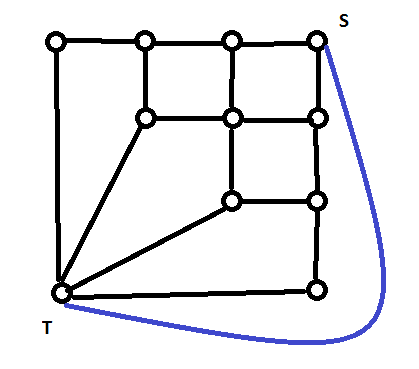
最后在对偶图上去掉$S'-T'$边后,从$S'$到$T'$跑一个最短路就是答案了。
需要注意的是,最短路的长度可能超过$1\times 10^9$,所以不妨在求最短路时直接就不走边权为$\infty$的边。

#include <queue> #include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef pair<ll,int> pli; typedef pair<int,int> pii; const int N=505; const int oo=1<<30; const ll OO=1LL<<60; int n,m; int e[N][N][2]; vector<pii> v[N*N]; inline void add(int x,int y,int w) { v[x].push_back(pii(y,w)); v[y].push_back(pii(x,w)); } ll d[N*N]; priority_queue<pli,vector<pli>,greater<pli> > Q; int main() { for(int i=1;i<N;i++) for(int j=1;j<N;j++) for(int k=0;k<2;k++) e[i][j][k]=oo; scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { char dir; int x,y,c; scanf("%d%d",&x,&y); dir=getchar(); while(dir!='L' && dir!='R') dir=getchar(); scanf("%d",&c); if(dir=='L') e[x][y][0]=c; //vertical else e[x][y-1][1]=c; //horizontal } int s=(n-1)*(n-1)+1,t=s+1; for(int i=1;i<n;i++) { for(int j=i;j<n-1;j++) { int id=(i-1)*(n-1)+j,w=e[i][j+1][0]; add(id,id+1,w); } add(i*(n-1),s,e[i][n][0]); } for(int i=1;i<n;i++) { add(i,t,e[1][i][1]); for(int j=1;j<i;j++) { int id=(j-1)*(n-1)+i,w=e[j+1][i][1]; add(id,id+n-1,w); } } for(int i=1;i<=t;i++) d[i]=OO; d[s]=0; Q.push(pli(0,s)); while(!Q.empty()) { ll D=Q.top().first; int x=Q.top().second; Q.pop(); if(D>d[x]) continue; for(int i=0;i<v[x].size();i++) { int y=v[x][i].first,w=v[x][i].second; if(w<oo && D+w<d[y]) { d[y]=D+w; Q.push(pli(d[y],y)); } } } printf("%lld\n",d[t]==OO?-1:d[t]); return 0; }
J. Just Shuffle (牛客 5667J)
由于保证$k$是一个很大的质数,那么任意循环节长度$len$都会与$k$互质,这可以保证对于$A$找出的循环节就是$P$中的循环节(只不过排列不同)。
于是就需要考虑如何对每个环分别构造了。
考虑假设$P=\{2,3,4,5,6,7,1\}$,进行$3$次置换后会得到$A=\{4,5,6,7,1,2,3\}$。这时,对$A$从$1$开始找环,能够得到$A'=\{4,7,3,6,2,5,1\}$。可以看出,$P[-1]=A'[len-1]=1$,$P[0]=A'[(6+5)mod\ 7]=2$,$P[2]=A'[(6+5\times 2)mod\ 7]=3$,$P[3]=A'(6+5\times 3)mod\ 7]=4$,也就是说$P$可以通过在$A'$上隔着相等距离$L=5$选数而得到。于是从$1$循环到$len$求合法的间隔距离即可,若出现多个则不存在合法方案。

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int N=100005; int n,k; int a[N]; bool vis[N]; int ans[N]; int main() { scanf("%d%d",&n,&k); for(int i=1;i<=n;i++) scanf("%d",&a[i]); bool flag=true; for(int i=1;i<=n;i++) { if(vis[i]) continue; vector<int> v; int p=a[i]; while(!vis[p]) { v.push_back(p),vis[p]=true; p=a[p]; } int L=-1,len=v.size(); for(int i=1;i<=len;i++) if(1LL*(k%len)*i%len==1) { if(L!=-1) flag=false; L=i; } int cur=len-1; for(int i=0;i<len;i++) { int nxt=(cur+L)%len; ans[v[cur]]=v[nxt],cur=nxt; } } if(!flag) printf("-1\n"); else for(int i=1;i<=n;i++) printf("%d%c",ans[i],i==n?'\n':' '); return 0; }
K. Keyboard Free (牛客 5667K)
卡了半天精度,结果发现是算的有问题...
这题直接算是比较困难的,可以考虑先枚举、再积分。
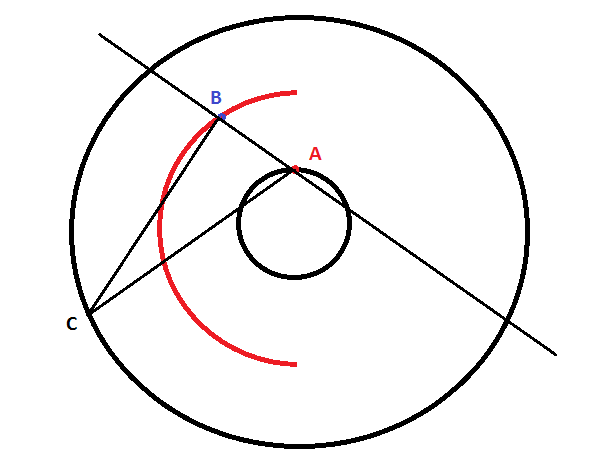
不妨让A点一直处于$(0,r_A)$,那么根据对称性,我们只需要在$x<0$的半圆弧上取$B$点。此时将AB边作为三角形的底边,那么我们需要计算在半径为$r_C$的圆周上取C点时,到AB边的高的期望。
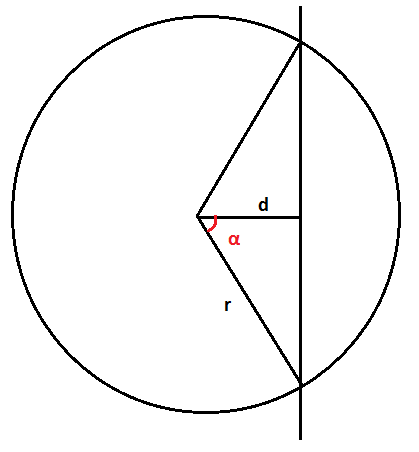
首先可以求出原点到AB所在直线的距离$d$,利用$d=\overrightarrow{OA}\times \overrightarrow{OB}\cdot \frac{1}{|AB|}$即可。那么半圆心角$\alpha=acos(\frac{d}{r})$。
不妨只计算$\theta\in [0,\pi]$的情况,因为另一半只是简单对称。当$\theta\in [0,\alpha]$时,高为$r(cos\theta-cos\alpha)$;当$\theta\in [\alpha,\pi]$时,高为$r(cos\alpha-cos\theta)$。于是对两部分分别积分。
\[\int_{0}^{\alpha}r(cos\theta-cos\alpha)d\theta=r(sin\theta-\theta\cdot cos\alpha)|_0^{\alpha}=r(sin\alpha-\alpha cos\alpha)\]
\[\int_{\alpha}^{\pi}r(cos\alpha-cos\theta)d\theta=r(\theta\cdot cos\alpha-sin\theta)|_{\alpha}^{\pi}=r[(\pi-\alpha) cos\alpha-(sin\pi-sin\alpha)]\]
两者合并起来就是$r[2sin\alpha+(\pi-2\alpha)cos\alpha]$。期望的话需要再除以$\pi$。
然后这里有一个小坑点,因为B在取点时只取了半圆弧,所以半圆弧的两端点均只产生$\frac{1}{2}$倍的贡献。如果取的是整圆就没这个问题了。
(long double运算好慢啊...如果不是很卡精度,用double就够了)

#include <cmath> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef double ld; const ld pi=acos(-1.0); const ld eps=0.0000001; struct Point { ld x,y; Point(ld a=0.0,ld b=0.0) { x=a,y=b; } }; inline Point operator -(Point X,Point Y) { return Point(X.x-Y.x,X.y-Y.y); } inline ld cross(Point X,Point Y) { return X.x*Y.y-X.y*Y.x; } inline ld pw2(ld x) { return x*x; } inline ld dist(Point X,Point Y) { return sqrt(pw2(X.x-Y.x)+pw2(X.y-Y.y)); } int r[3]; int main() { int T; scanf("%d",&T); while(T--) { for(int i=0;i<3;i++) scanf("%d",&r[i]); sort(r,r+3); double ans=0.0; Point A(0,r[0]); for(int i=0;i<=2000;i++) { ld angle=i*pi/2000.0; Point B(-r[1]*sin(angle),r[1]*cos(angle)); ld d; if(dist(A,B)>eps) d=abs(cross(A,B))/dist(A,B); else d=r[0]; ld a=acos(d/r[2]); ld res=0.0; res=r[2]*(sin(a)*2+cos(a)*(pi-a*2)); if(i==0 || i==2000) res/=2.0; ans=ans+res*dist(A,B); } printf("%.10f\n",double(ans/4000.0/pi)); } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号