补题:2020牛客暑期多校训练营(第一场)
Solved:4/10
Upsolved:10/10
A. B-Suffix Array (牛客 5666A)
两种做法:一种是利用性质后转为求SA,另一种是Hash+二分。
根据论文 Parameterized Suffix Arrays for Binary Strings,题目中对于后缀的B-function排序,可以通过将其进行一点类似的转化后直接用后缀数组来求。
转化是这样进行的:将字符串$s_1...s_n$转化为数组$b_1...b_n$,其中$b_i=min_{j>i,s[i]=s[j]}\{j-i\}$,若不存在$j$则$b_i=n+1$(只要是一个正常取不到的大数就行)。同时令$b_{n+1}=n+2$,这样使得$sa[1]=n$。倒序输出$sa$数组即可。

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int N=100005; int sa[N],rk[N]; //sa[i]: 第i小的后缀的开头位置 //rk[i]: 后缀s[i..n]的rank int tmp[N<<1],top[N]; void quicksort(int n,int m) { for(int i=1;i<=m;i++) top[i]=0; for(int i=1;i<=n;i++) top[rk[i]]++; for(int i=1;i<=m;i++) top[i]=top[i-1]+top[i]; for(int i=n;i>=1;i--) sa[top[rk[tmp[i]]]--]=tmp[i]; } void getsa(int *s,int n,int lim) { for(int i=1;i<=n;i++) rk[i]=s[i],tmp[i]=i; for(int i=n+1;i<=2*n;i++) tmp[i]=0; quicksort(n,lim); for(int i=1;i<n;i<<=1) { int cnt=0; for(int j=n-i+1;j<=n;j++) tmp[++cnt]=j; for(int j=1;j<=n;j++) if(sa[j]>i) tmp[++cnt]=sa[j]-i; quicksort(n,max(cnt,lim)); for(int j=1;j<=n;j++) swap(rk[j],tmp[j]); rk[sa[1]]=cnt=1; for(int j=2;j<=n;j++) { if(tmp[sa[j]]!=tmp[sa[j-1]] || tmp[sa[j]+i]!=tmp[sa[j-1]+i]) cnt++; rk[sa[j]]=cnt; } if(cnt==n) break; } } int n; char s[N]; int b[N]; int main() { while(~scanf("%d",&n)) { scanf("%s",s+1); int pos[2]={n+1,n+1}; for(int i=n;i>=1;i--) { b[i]=(pos[s[i]-'a']>n?n+1:pos[s[i]-'a']-i); pos[s[i]-'a']=i; } b[n+1]=n+2; getsa(b,n+1,n+2); for(int i=n+1;i>=1;i--) if(sa[i]<=n) printf("%d%c",sa[i],i==1?'\n':' '); } return 0; }
Hash就比较暴力了。不过都比较卡常。
首先我们可以对于$s_1...s_n$先求出题目中B-function的$b_1...b_n$。如果我们比较两个后缀,其实只会在这个B function上将 'a','b'两个字符第一次出现位置 的$b_i$变为$0$,其余的$b_i$保持不变。那么我们在排序时,可以二分出两个B-suffix中第一个$b_i$不等的位置,只比较这个位置上的值即可,判断前缀是否相等用hash就能完成。
其实还有另一种实现办法。如果我们认为第一个字母一定为'a',那么可以仅对'a'出现的位置进行hash,而'b'出现的位置则也相应确定。此时只需要对'a'、'b'分别预处理hash,每次二分时根据首字母选用对应的hash。
B. Infinite Tree (牛客 5666B)
首先可以发现,真正可能选为根节点的地方,仅为$i!$或$LCA(i!,j!)$。于是建虚树。
可以先建一棵$m=10$的树看一看LCA的条件。
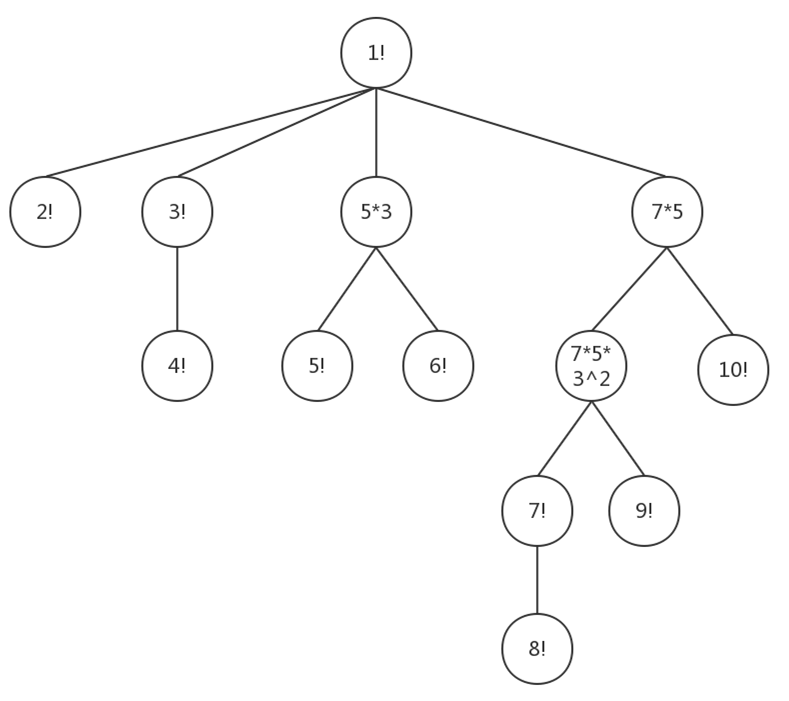
能够发现,$i!$与$(i-1)!$分叉的位置是,$(i-1)!$所有大于等于$maxdiv(i)$的质因子之积(质因子可重复)。虽然判断条件都为这个,但是不同写法的实现难度差距很大,自己写炸之后学习了别人的写法,利用了树上深度来判断弹栈的终止。
之后就是简单的树上dfs了。若向儿子走,那么$\Delta ans=(dep[son]-dep[x])\cdot (\sum w_i-\sum_{i\in subtree(son)}w_i)$。

#include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=100005; int n; ll w[2*N]; int mindiv[N]; int t[N]; inline int lowbit(int x) { return x&(-x); } inline void add(int k,int x) { for(int i=k;i<=n;i+=lowbit(i)) t[i]+=x; } inline int query(int k) { int ans=0; for(int i=k;i;i-=lowbit(i)) ans+=t[i]; return ans; } int tot,dep[N*2]; int top,st[N],pos[N]; vector<int> v[N*2]; void build(int n) { tot=n,st[top=1]=1; for(int i=1;i<=n;i++) t[i]=0; for(int i=2,j;i<=n;i++) { dep[i]=dep[i-1]+1; for(j=i;j!=mindiv[j];j/=mindiv[j]) dep[i]++; pos[i]=query(n)-query(j-1); for(j=i;j!=1;j/=mindiv[j]) add(mindiv[j],1); } for(int i=2;i<=n;i++) { while(top>1 && dep[st[top-1]]>=pos[i]) { v[st[top-1]].push_back(st[top]); top--; } if(dep[st[top]]!=pos[i]) { dep[++tot]=pos[i]; v[tot].push_back(st[top]); st[top]=tot; } st[++top]=i; } while(top>1) { v[st[top-1]].push_back(st[top]); top--; } } void getsz(int x) { for(int i=0;i<v[x].size();i++) { int y=v[x][i]; getsz(y); w[x]+=w[y]; } } void dfs(int x,ll val,ll &ans) { ans=min(val,ans); for(int i=0;i<v[x].size();i++) { int y=v[x][i],len=dep[y]-dep[x]; dfs(y,val+(w[1]-2*w[y])*len,ans); } } int main() { for(int i=1;i<N;i++) mindiv[i]=i; for(int i=2;i*i<N;i++) for(int j=i;j<N;j+=i) mindiv[j]=min(mindiv[j],i); while(~scanf("%d",&n)) { build(n); for(int i=1;i<=n;i++) scanf("%lld",&w[i]); for(int i=n+1;i<=tot;i++) w[i]=0; ll ans=0; for(int i=1;i<=n;i++) ans+=1LL*w[i]*dep[i]; getsz(1); dfs(1,ans,ans); printf("%lld\n",ans); for(int i=1;i<=tot;i++) v[i].clear(); } return 0; }
C. Domino (牛客 5666C)
又是一个论文题,链接见:Distances in Domino Flip Graphs。
感觉没啥意思,没有很多推广的样子...那么就变成锻炼阅读英语论文了。
具体的算法参考Page 7的Figure 5,对于所有格子周围的点计算$h_T(v)$(共$(n+1)\times (m+1)$个点)。计算方法就是,从$(0,0)$出发,不穿过任何Domino到达$(x,y)$经过的正向边数$-$反向边数(即论文Page 7中的$h_T(v)=\sum_{i=1}^n o(e_i)$)。(假装)能够证明通过任意路径到达$(x,y)$得出的$h_T$值相等。最后,两个Domino覆盖$T,T'$间的距离为$\frac{1}{4}\sum |h_T(v)-h_{T'}(v)|$。
所以代码中真正要做的工作就是把同一块Domino粘一起来判断是否穿过,然后bfs即可。貌似也有不用bfs的实现。

#include <queue> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef pair<int,int> pii; const int N=1005; const int dx[2]={1,0},dy[2]={0,1}; inline char getch() { char ch=getchar(); while(ch!='|' && ch!='-') ch=getchar(); return ch; } int n,m; char map[N][N],ord[N][N]; queue<pii> Q; bool vis[N][N]; inline bool inboard(int x,int y) { return (x>=0 && x<=n && y>=0 && y<=m); } void calc(int *dist) { for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) map[i][j]=getch(),ord[i][j]=0; for(int i=0;i<=n;i++) for(int j=0;j<=m;j++) vis[i][j]=false; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { if(map[i][j]=='-' && ord[i][j]==0) ord[i][j]=1,ord[i][j+1]=2; if(map[i][j]=='|' && ord[i][j]==0) ord[i][j]=1,ord[i+1][j]=2; } vis[0][0]=true,Q.push(pii(0,0)); while(!Q.empty()) { int x=Q.front().first,y=Q.front().second; Q.pop(); for(int i=0;i<2;i++) { int nx=x+dx[i],ny=y+dy[i]; if(!inboard(nx,ny) || vis[nx][ny]) continue; if(i==0 && y<m && map[x+1][y]=='-' && map[x+1][y+1]=='-' && ord[x+1][y]==1 && ord[x+1][y+1]==2) //down continue; if(i==1 && x<n && map[x][y+1]=='|' && map[x+1][y+1]=='|' && ord[x][y+1]==1 && ord[x+1][y+1]==2) //right continue; vis[nx][ny]=true; Q.push(pii(nx,ny)); dist[nx*m+ny]=dist[x*m+y]+((x+y)%2==0?1:-1)*(i==0?1:-1); } } } int ds[N*N],dt[N*N]; //height int main() { while(~scanf("%d%d",&n,&m)) { calc(ds); calc(dt); int ans=0; for(int i=0;i<=n;i++) for(int j=0;j<=m;j++) ans+=abs(ds[i*m+j]-dt[i*m+j]); printf("%d\n",ans/4); } return 0; }
D. Quadratic Form (牛客 5666D)
这题考察的是线性规划的求解。线性规划的标准形式如下(其中$X\in R^n$):
\[\left\{\begin{array}{**lr**} min\ f(X)\\c_i(X)\leq 0, & i=1,2,...\\h_j(X)=0, & j=1,2,...\end{array}\right.\]
那么将这道题目的条件套进去,就能够写出:
\[\left\{\begin{array}{**lr**} min\ -b^TX\\X^TAX-1\leq 0\end{array}\right.\]
此时,拉格朗日函数为$L(X,\mu)=-b^TX+\mu(X^TAX-1)$,设最优解为$X^*,\mu^*$。
考虑代入KTT条件:
\[\left\{\begin{array}{**lr**} \nabla_X L(X^*,\mu^*)=-b^T+\mu^*{X^*}^T(A+A^T)=0 & (1)\\ \nabla_{\mu}L(X^*,\mu^*)={X^*}^TAX^*-1=0 & (2)\\ \mu^*\geq 0 &(3)\\ \mu^*({X^*}^TAX^*-1)\leq 0 & (4)\end{array}\right.\]
有了$(2)$,就可以直接无视$(4)$了。$(3)$对于求解没有太多帮助。
由$(1),(2)$,再加上$A$对称,能够一同推出:$-b^TX^*-\mu^*{X^*}^T(A+A^T)X^*=-b^TX^*+\mu^*\cdot 2=0$,从而得到:
\[\begin{array}{**lr**} \mu^*=\frac{1}{2}b^TX^* & (5)\end{array}\]
而又由$(1)$,能够推出:
\[\begin{array}{**lr**} {X^*}^T=\frac{1}{\mu^*}b^T(A+A^T)^{-1}\end{array}\]
整理一下,再转置,就是:
\[\begin{array}{**lr**} X^*=\frac{A^{-1}b}{2\mu^*} &(6)\end{array}\]
综合$(1),(6)$,得到:
\[b^TX^*=b^T\frac{A^{-1}b}{2\mu^*}=b^T\frac{A^{-1}b}{b^TX^*}\]
即有$(b^TX^*)^2=b^TA^{-1}b$。

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; //如果为了求逆,N需要开到原来的两倍 const int N=405; const int MOD=998244353; inline int quickpow(int x,int k) { int res=1; while(k) { if(k&1) res=1LL*res*x%MOD; x=1LL*x*x%MOD; k>>=1; } return res; } inline int rev(int x) { return quickpow(x,MOD-2); } struct Determinant { int a[N][N]; Determinant() { memset(a,0,sizeof(a)); } int value(int n) { int ans=1; for(int i=0;i<n;i++) for(int j=i+1;j<n;j++) while(a[j][i]) { int mul=a[i][i]/a[j][i]; for(int k=i;k<n;k++) { a[i][k]=(a[i][k]-1LL*a[j][k]*mul%MOD+MOD)%MOD; swap(a[i][k],a[j][k]); } ans=-ans; } for(int i=0;i<n;i++) ans=1LL*ans*a[i][i]%MOD; return (ans+MOD)%MOD; } int reverse(int n) { for(int i=0;i<n;i++) for(int j=n;j<2*n;j++) a[i][j]=(j-n==i?1:0); for(int i=0;i<n;i++) { int pos=i; if(pos<n && !a[pos][i]) pos++; if(pos==n) return 0; int mul=rev(a[pos][i]); for(int j=0;j<2*n;j++) { swap(a[i][j],a[pos][j]); a[i][j]=1LL*a[i][j]*mul%MOD; } for(int j=0;j<n;j++) if(j!=i) { mul=a[j][i]; for(int k=i;k<2*n;k++) a[j][k]=(a[j][k]-1LL*mul*a[i][k]%MOD+MOD)%MOD; } } for(int i=0;i<n;i++) for(int j=0;j<n;j++) a[i][j]=a[i][j+n]; return 1; } }; int n; Determinant A; int b[N],tmp[N]; int main() { while(~scanf("%d",&n)) { memset(tmp,0,sizeof(tmp)); for(int i=0;i<n;i++) for(int j=0;j<n;j++) scanf("%d",&A.a[i][j]); for(int i=0;i<n;i++) scanf("%d",&b[i]); A.reverse(n); for(int i=0;i<n;i++) for(int j=0;j<n;j++) tmp[i]=(tmp[i]+1LL*b[j]*A.a[j][i])%MOD; int ans=0; for(int i=0;i<n;i++) ans=(ans+1LL*b[i]*tmp[i])%MOD; printf("%d\n",ans); } return 0; }
E. Counting Spanning Trees (牛客 5666E)
论文题,原论文见:https://arxiv.org/pdf/0706.2918.pdf。
首先,满足题目中条件的二分图被称为Ferrers图。记二分图$G$中的两个点集为$U=\{u_1,...,u_n\},V=\{v_1,...,v_m\}$,记度数分别为$\lambda_1,...,\lambda_n$和$\lambda'_1,...,\lambda'_m$,此图为Ferrers图的严格的条件为:
1. 若$(u_i,v_j)$边存在则有$(u_p,v_q)$边均存在($1\leq p\leq i,1\leq q\leq j$),换句话说也就是$\lambda_i$单调减且与$v_1,...,v_{\lambda_i}$均有边。
2. 无孤立点。
此二分图中的度数$\tau (G)=\prod_{i=2}^n \lambda_i\prod_{j=2}^m \lambda'_j$(不知道有没有感性的理解)。
回到本题中,就需要先将$a_i$按从大到小排序,然后对二分图的另一侧算度数,之后去掉两侧最大的度数后将度数相乘即可。

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int N=100005; int n,m,mod; int a[N],ord[N],b[N]; int main() { while(~scanf("%d%d%d",&n,&m,&mod)) { for(int i=1;i<=n;i++) scanf("%d",&a[i]); sort(a+1,a+n+1); for(int i=1;i<=m;i++) b[i]=n-(lower_bound(a+1,a+n+1,i)-a)+1; ll ans=1; for(int i=1;i<n;i++) ans=ans*a[i]%mod; for(int i=2;i<=m;i++) ans=ans*b[i]%mod; printf("%lld\n",ans); } return 0; }
F. Infinite String Comparision (牛客 5666F)
签到题。把最长的串复制一遍,把另一个串也补全到这个长度,比较即可。

#include <cstdio> #include <cstring> using namespace std; const int N=200005; int solve(char *s,int n,char *t,int m) { int lim=n*2; for(int i=n+1;i<=lim;i++) s[i]=s[(i-1)%n+1]; for(int i=m+1;i<=lim;i++) t[i]=t[(i-1)%m+1]; for(int i=1;i<=lim;i++) if(s[i]!=t[i]) return s[i]<t[i]?-1:1; return 0; } int n,m,ans; char s[N],t[N]; int main() { while(~scanf("%s%s",s+1,t+1)) { n=strlen(s+1),m=strlen(t+1); if(n>m) ans=solve(s,n,t,m); else ans=-solve(t,m,s,n); if(ans==0) printf("=\n"); if(ans==-1) printf("<\n"); if(ans==1) printf(">\n"); } return 0; }
G. 八仙过海,各显神通 (牛客 5666G)
看到题目中定义的乘,就应该考虑是否满足交换律、结合律。其实是满足的,因为可以每个向量都可以写成矩阵的形式。
\[\begin{pmatrix} a_0 & a_1 & a_2\\ a_1 & a_2 & a_0\\ a_2 & a_0 & a_1\end{pmatrix}\]
队友lyy在现场推了个神仙结论,就是题目中规定的向量乘有$P^2-1$的公共循环节(对于任意向量)。于是就可以将每个向量的幂次降到__int128的范围内了,可以使用快速幂。
据他所说,他是受到了51nod 1195的启发,认为公共循环节一定在$P^3$级别或以内,然后对于$P$较小的素数打表发现的规律。对于合数,他觉得应该可以用积性函数推出类似的结论。

#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; typedef __int128 i128; typedef unsigned int ui; const int N=100005; const int P=998244353; const ll PP=1LL*P*P-1; struct Vector { ll a[3]; Vector(ll x=0,ll y=0,ll z=0) { a[0]=x,a[1]=y,a[2]=z; } }; inline Vector operator *(const Vector &X,const Vector &Y) { Vector res; res.a[0]=(X.a[0]*Y.a[0]+X.a[1]*Y.a[2]+X.a[2]*Y.a[1])%P; res.a[1]=(X.a[1]*Y.a[0]+X.a[2]*Y.a[2]+X.a[0]*Y.a[1])%P; res.a[2]=(X.a[2]*Y.a[0]+X.a[0]*Y.a[2]+X.a[1]*Y.a[1])%P; return res; } inline i128 quickpow(i128 x,ll t) { i128 res=1; while(t) { if(t&1) res=res*x%PP; x=x*x%PP; t>>=1; } return res; } inline Vector quickpow(Vector x,ll t) { Vector res(1,0,0); while(t) { if(t&1) res=res*x; x=x*x; t>>=1; } return res; } int n,m,q,z0,a,b; Vector v[N]; i128 pw2[10]; int main() { scanf("%d%d%d%d%d%d",&n,&m,&q,&z0,&a,&b); for(int i=0;i<10;i++) pw2[i]=quickpow(2,32*i); ui z=z0; for(int i=1;i<=n;i++) for(int j=0;j<3;j++) { z=z*a+b; v[i].a[j]=z%P; } while(q--) { Vector ans(1,0,0); for(int i=1;i<=n;i++) { i128 pw=0; for(int j=0;j<m;j++) { z=z*a+b; pw=(pw+1LL*z*pw2[j])%PP; } ans=ans*quickpow(v[i],pw); } printf("%lld %lld %lld\n",ans.a[0],ans.a[1],ans.a[2]); } return 0; }
H. Minimum-cost Flow (牛客 5666H)
对于每一个询问$u,v$,我们相当于在原图中求流量为$\frac{v}{u}$的最小费用流。我们只要把所有整数流量的最小费用流求出来(每次跑出一个增广路的时候存一下),对于每个询问在所有方案里面二分就行了。
假设所有方案中,第$i$个的总流量为$f_i$、费用为$c_i$(均有$f_i+1=f_{i+1}$,因为原图中每边容量为$1$),那么最终要输出的答案为:
\[c_i\cdot \frac{u}{v}+(\frac{v}{u}-f_i)\cdot \frac{c_{i+1}-c_i}{f_{i+1}-f_i}\cdot \frac{u}{v}=\frac{c_iu+(v-uf_i)(c_{i+1}-c_i)}{v}\]

#include <cstdio> #include <algorithm> #include <vector> #include <cstring> #include <queue> using namespace std; struct Edge { int to,cap,cost,rev; Edge(int a,int b,int c,int d) { to=a,cap=b,cost=c,rev=d; } }; typedef long long ll; typedef pair<int,int> pii; const int INF=1<<30; const int N=205; int n,m; vector<Edge> v[N]; inline void Add(int from,int to,int cap,int cost) { v[from].push_back(Edge(to,cap,cost,v[to].size())); v[to].push_back(Edge(from,0,-cost,v[from].size()-1)); } int h[N],dist[N]; int prevv[N],preve[N]; vector<pii> ans; int min_cost_flow(int s,int t,int f) { int res=0; memset(h,0,sizeof(h)); while(f) { priority_queue<pii,vector<pii>,greater<pii> > Q; for(int i=0;i<N;i++) dist[i]=INF; dist[s]=0; Q.push(pii(0,s)); while(!Q.empty()) { pii p=Q.top(); Q.pop(); int cur=p.second; if(dist[cur]<p.first) continue; for(int i=0;i<v[cur].size();i++) { Edge &e=v[cur][i]; if(e.cap>0 && dist[e.to]>dist[cur]+e.cost+h[cur]-h[e.to]) { dist[e.to]=dist[cur]+e.cost+h[cur]-h[e.to]; prevv[e.to]=cur; preve[e.to]=i; Q.push(pii(dist[e.to],e.to)); } } } if(dist[t]==INF) return -1; for(int i=0;i<=n;i++) h[i]+=dist[i]; int d=f; for(int i=t;i!=s;i=prevv[i]) d=min(d,v[prevv[i]][preve[i]].cap); f-=d; res+=d*h[t]; ans.push_back(pii(INF-f,res)); for(int i=t;i!=s;i=prevv[i]) { Edge &e=v[prevv[i]][preve[i]]; e.cap-=d; v[i][e.rev].cap+=d; } } return res; } int main() { while(~scanf("%d%d",&n,&m)) { ans.clear(); for(int i=1;i<=n;i++) v[i].clear(); for(int i=1;i<=m;i++) { int x,y,c; scanf("%d%d%d",&x,&y,&c); Add(x,y,1,c); } ans.push_back(pii(0,0)); min_cost_flow(1,n,INF); int q; scanf("%d",&q); while(q--) { ll ui,vi; scanf("%lld%lld",&ui,&vi); if(vi>ui*ans.back().first) { printf("NaN\n"); continue; } int l=0,r=ans.size()-1,mid,res=-1; while(l<r) { mid=(l+r)>>1; if(vi>ui*ans[mid].first) l=mid+1,res=mid; else r=mid; } ll num=ans[res].second; ll dnum=vi; num=num*ui+(vi-ui*ans[res].first)*(ans[res+1].second-ans[res].second); ll gcd=__gcd(num,dnum); printf("%lld/%lld\n",num/gcd,dnum/gcd); } } return 0; }
I. 1 or 2 (牛客 5666I)
当$d_i\leq 2$时,可以利用对称性用最大流求解(并不是十分确定正确性)。但是当$d_i>2$时,就变成了HDU 3551,需要使用带花树(一般图匹配算法)。
将每条边$(x,y)$拆成$(x_1,e),(e,e'),(e',y_1)$三条边(若$d_x=2$,则还需要拆出$(x_2,e)$;$d_y=2$类似),然后跑一遍带花树,判断最大匹配数是否等于$\frac{1}{2}\sum d_i$即可。
举个例子来说明这个方法的正确性。假如输入为:
3 3 2 1 1 1 2 1 3 2 3
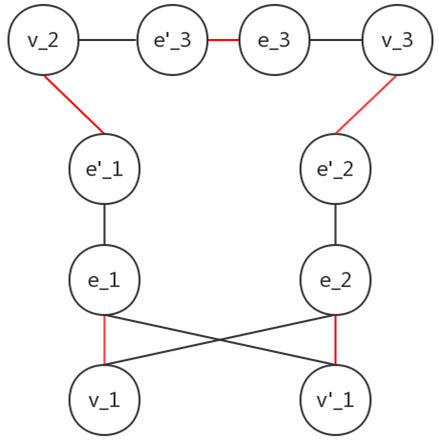
上图的红线给出了一种最大匹配的方案。可以看出,在有最大匹配时,每个节点的度数均等于$d_i$;若一条原图中的边在最终方案中出现,则拆出的边中有$2$条被选中(为$(v_j,e_i),(e'_i,v_k)$,其中$v_j,v_k$也可为$v'_j,v'_k$);若一条原图中的边在最终方案中未出现,则拆出的边中有$1$条被选中(为$(e_i,e'_i)$)。
在答案为Yes时,共有$\frac{1}{2}\sum d_i$条原图中的边出现、$m-\frac{1}{2}\sum d_i$条未出现,则在拆边后的图中共有$2\cdot \frac{1}{2}\sum d_i+ 1\cdot (m-\frac{1}{2}\sum d_i)=m+\frac{1}{2}\sum d_i$条边被选中(即最大匹配数)。而拆边后的图中共有$2m+\sum d_i$个节点。故回答为Yes的条件是 $2\times $最大匹配数=拆点数。
一般图匹配还是博大精深的,有不少类似网络流的蛇皮建图,有必要更加深入地学习。

#include <queue> #include <cstdio> #include <vector> #include <cstring> #include <algorithm> using namespace std; const int N=505; //用并查集维护点是否在奇环内 int fa[N]; inline int find(int a) { if(fa[a]==a) return a; return fa[a]=find(fa[a]); } int n,m; vector<int> v[N]; //vis: 染色标记+访问标记 //pre: 增广路的前一个点 //match: 与哪个点匹配 int vis[N],pre[N],match[N]; queue<int> Q; //cnt: 标记总数 //tag: 在求lca时,给路径打上标记 int cnt,tag[N]; int lca(int x,int y) { for(++cnt;;swap(x,y)) if(x) { x=find(x); if(tag[x]==cnt) return x; tag[x]=cnt,x=pre[match[x]]; } } void blossom(int x,int y,int _lca) { while(find(x)!=_lca) { pre[x]=y,y=match[x]; if(vis[y]==2) vis[y]=1,Q.push(y); if(find(x)==x) fa[x]=_lca; if(find(y)==y) fa[y]=_lca; x=pre[y]; } } bool augment(int x,int id) { for(int i=1;i<=id;i++)//not template fa[i]=i,vis[i]=pre[i]=0; while(!Q.empty()) Q.pop(); vis[x]=1; Q.push(x); while(!Q.empty()) { x=Q.front(); Q.pop(); for(int i=0;i<v[x].size();i++) { int y=v[x][i],last; if(find(x)==find(y) || vis[y]==2) continue; if(!vis[y]) { vis[y]=2,pre[y]=x; if(!match[y]) //y成为增广路的终点 { for(x=y;x;x=last) last=match[pre[x]],match[x]=pre[x],match[pre[x]]=x; return true; } vis[match[y]]=1; Q.push(match[y]); } else { int _lca=lca(x,y); blossom(x,y,_lca),blossom(y,x,_lca); } } } return false; } int d[N]; int idx[N][2]; int main() { while(~scanf("%d%d",&n,&m)) { cnt=0; memset(tag,0,sizeof(tag)); memset(match,0,sizeof(match)); int id=0,sum=0; for(int i=1;i<=n;i++) { scanf("%d",&d[i]); for(int j=1;j<=d[i];j++) idx[i][j]=++id; } sum=id; for(int i=1;i<=m;i++) { int x,y; scanf("%d%d",&x,&y); for(int j=1;j<=d[x];j++) v[idx[x][j]].push_back(id+1),v[id+1].push_back(idx[x][j]); for(int j=1;j<=d[y];j++) v[idx[y][j]].push_back(id+2),v[id+2].push_back(idx[y][j]); v[id+1].push_back(id+2),v[id+2].push_back(id+1); id+=2; } int ans=0; for(int i=1;i<=id;i++) if(!match[i] && augment(i,id)) ans++; if(ans*2==id) printf("Yes\n"); else printf("No\n"); for(int i=1;i<=id;i++) v[i].clear(); } return 0; }
J. Easy Integration (牛客 5666J)
推导见:某作业帮答案
如果放到现场赛真的会变成签到题吗?深表怀疑。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号