第4章 语法分析
自顶向下语法分析
消除回溯
- 路标法:设有规则U∷=a1V1|a2V2|…|anVn,若ai为互不相同的终结符时,将ai作为路标,当被分析符号串为ai时,便可按规则U∷=aiVi往下分析,这样可以消除回溯。
- 提取左因子法:当文法不满足上述路标法条件,即规则右部首符号相同时,可以采用提取左因子法对文法进行改写。
消除直接左递归
- 重复表示法:使用扩充BNF重新表示规则
- 改写法:对A引入一个新的非终结符A′,将A∷=Aα|β等价写成A∷=βA′;A′∷=αA′|ε
消除间接左递归
对于间接左递归先将间接左递归变成直接左递归,然后消除直接左递归
例如:A ∷=aB|Bb(1);B ∷=Ac|d(2)
先将(1)代入(2)中,得B ∷=Bbc|aBc|d(3)
由此将(3)改写为:B ∷=(aBc|d);B′∷=bcB′|ε
LL(1)语法分析
LL(1)分析方法也是一种自顶向下不带回溯的分析方法,LL的意思是:从左到右扫描输入符号串并建立它的最左推导。数字1是指向前看一个符号来决定选择同一个非终结符的不同规则。
构造头终极符号集FIRST
FIRST(α)是α的所有可能推导的开头终结符或可能的ε。
对于文法中的每一个文法符X∈(VNUVT),构造FIRST(X)时,只要连续使用下列规则,直至每个FIRST集不再扩大为止。
- 若X∈VT,则FIRST(X)={X}。
- 若X∈VN,且有形如X∷=aα规则(a∈VT),或X∷=ε的规则,把a或(和)ε加入FIRST(X)中。
- 设文法G中有形如X∷=Y1Y2…Yk的规则,若Y1∈VN,则将FIRST(Y1)中一切非ε符号加进FIRST(X)中,若Y1=>*ε,则把Y2中首符号集FIRST(除ε外)也加入FIRST(X)中,如此继续下去,直到Yk-1=>*ε,则把Yk中首符号集(除ε外)也入FIRST(X)中。
- 若Y1,Y2…Yk每个非终结符号都可能推导出空符号串,即Y1,Y2…Yk=>*ε,则把ε也加进FIRST(X)中
构造后继终结符号集FOLLOW
FOLLOW(B)是所有句型中出现在紧接B之后的终结符或#。
对文法中每个非终结符B,为了构造FOLLOW(B),可反复应用如下规则,直到每个FOLLOW集不再扩大为止。
- 若B是文法的开始符号,令#∈FOLLOW(B)。
- 若文法中有形如A∷=αBβ的规则,且β≠ε,则将FIRST(β)中一切非ε符号加进FOLLOW(B)中。
- 若文法中有形如A∷=αB或A∷=αBβ的规则,且β=>*ε,则将FOLLOW(A)中全部终结符写入FOLLOW(B),其中α可以为ε。
构造分析表M
- 求出符号串FIRST集合和所有非终结符FOLLOW集合;
- 对于G中每一个规则A∷=α,可按如下算法确定表中各元素:
- 对FIRST(α)中每一终结符a,置M[A, a]=“A→α”;
- 若ε∈FIRST(α),则对属于FOLLOW(A)中的每一符号b (b为终结符或#),置M[A,b]=“A→α”;
- 把M中所有不能按规则①、②定义的元素均置为出错,置为空。
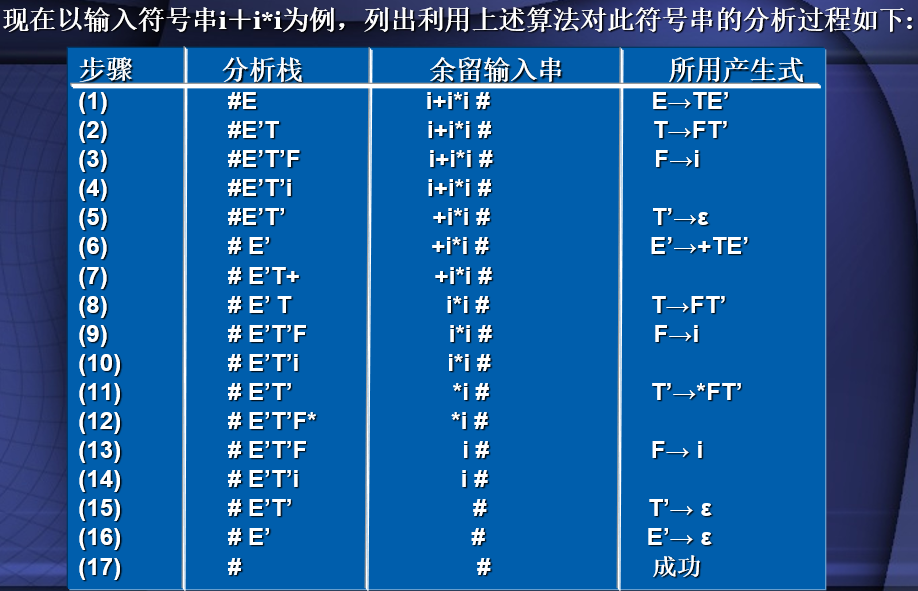
LL(1)分析符号串
- 分析栈从左到右是栈底到栈顶,栈底放置#,符号串从左到右是首元素和末尾元素,某尾放置#
- 每次分析栈顶元素遇到余留符号串首字符,并将分析表中规则右部倒序放入分析栈
- 如果栈顶元素和余留符号串首字符相同,则两者匹配去除,直到分析栈和预留符号串皆剩下#,则分析成功

LL(1)文法
- 一个文法G,如果它的分析表M不含多重定义入口,则称该文法是LL(1)文法。
- LL(1)文法是2型文法,但并不是所有2型文法都是LL(1)文法。
- LL(1)文法不是二义的,也不含左递归。
证明文法G是LL(1)文法,当且仅当G的任何两个规则A∷=α|β,满足下面条件:
- FIRST(α)∩ FIRST(β)=Ø,也就是α和β推导不出以某个同一终结符a为首的符号串。
- α和β中最多只有一个可能推出空串.
- 如果β=>*ε,那么α推出任何串不会以FOLLOW(A)中的终结符开始,即若β=>*ε则FIRST(α) ∩FOLLOW(A) =Ø。
自底向上语法分析
活前缀:是规范句型的一个前缀,不含有句柄后任何符号。
活前缀和句柄的关系
- 活前缀已包含句柄全部符号,用A∷=β·表示,意味着相应的分析动作应是用此规则进行归约,称可归约的活前缀。
- 活前缀中只含句柄一部分符号,用A∷=β1·β2表示,意味着β1已出现在栈顶,正期待着从余留输入串中看到能由β2推出的符号串。
- 活前缀不包含句柄的任何符号,用A∷=·β表示,意味着右部符号串β不在分析栈顶,正期待从余留输入串中由规则A∷=β的β所能推出的符号串。
LR(0)项目
- 对于形如A∷=β·项目, 因为它表明右部符号串β已出现在栈顶,此时相应分析动作应按规则进行归约,称此种项目为归约项目。
- 对于形如A∷=β1·aβ2,其中β1可以是ε,a是终结符,相应分析动作应将当前输入符号移入栈中,故称此项目为移进项目。
- 对于形如A∷=β1·Bβ2,其中β1可以是ε,B是非终结符,由于期待着从余留输入符号串中进行归约而得到B,称此类项目为待约项目。
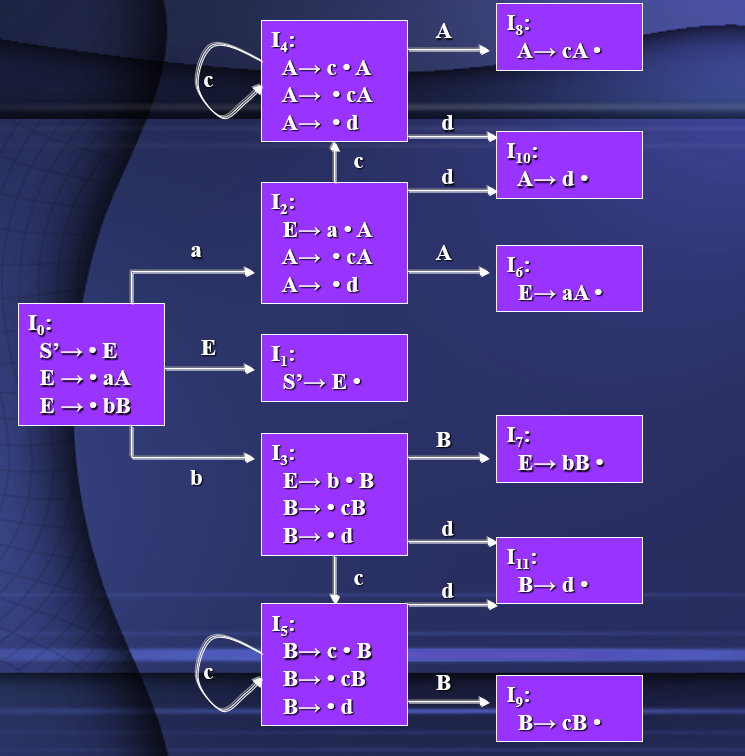
构造识别活前缀的NFA
- 拓广文法:设开始文法S′,将项目S′∷=·S称为项目集I0的基本项目。对于规则A∷=β对应项目数为|β|+1个,根据·号位置不同进行拓广文法;
- 闭包的构建(自我拓展):若状态中有形如A→β1·Bβ2的LR(0)项目,则将B→•x1|•x2|...|•xn所有项目加入此状态,重复以上过程,直至新产生的LR(0)项目圆点后全是总结符号位置(B∈VN);
- 延伸:状态中所有形如A→β1·αβ2的LR(0)项目(α可以是VN也可以是VT),标注一条箭弧(箭弧上的符号为α)延伸至新的状态,新状态中必会有A→β1α•β2的LR(0)项目。所有状态都要进行延伸,直至圆点后无符号或出现自回路为止。
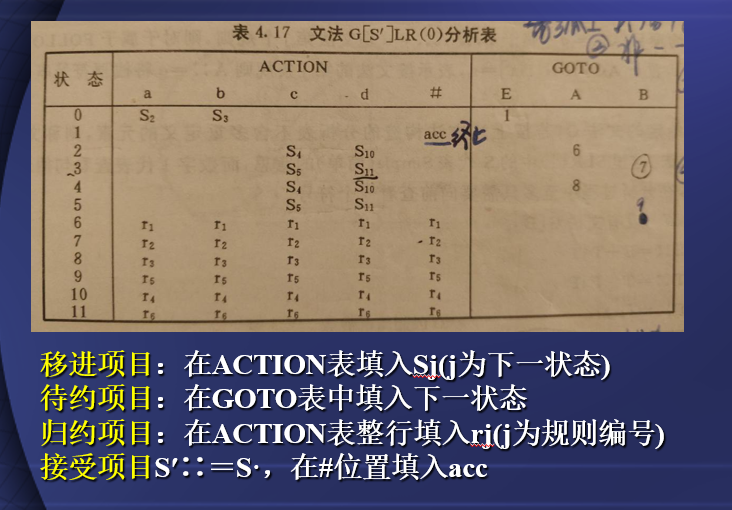
LR(0)分析表的构建
- 移进项目:在ACTION表填入Sj(j为下一状态)
- 待约项目:在GOTO表中填入下一状态
- 归约项目:在ACTION表整行填入rj(j为规则编号)
- 接受项目S′∷=S·,在#位置填入acc


根据分析表分析过程
- E∷=E+T
- E∷=T
- T∷=T*F
- T∷=F
- F∷=(E)
- F∷=i
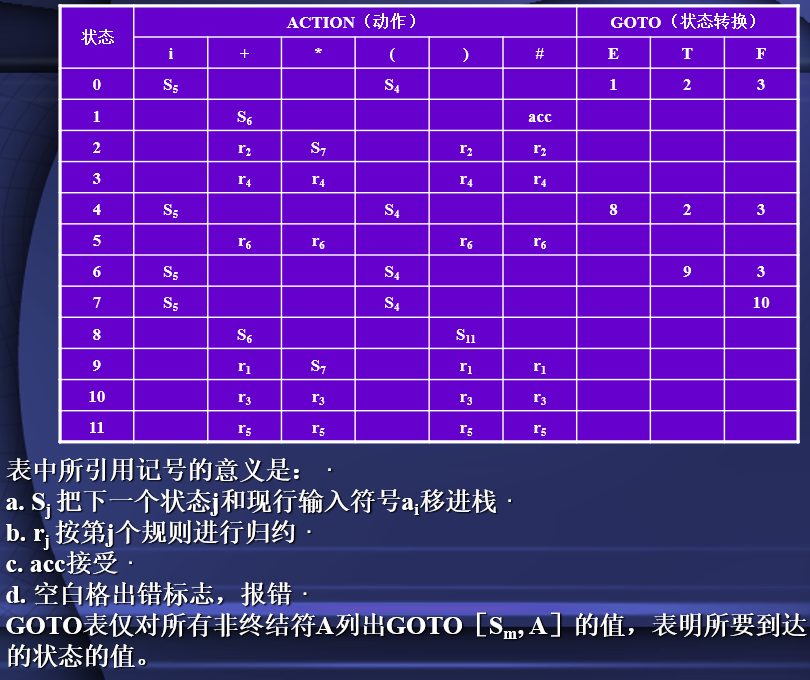
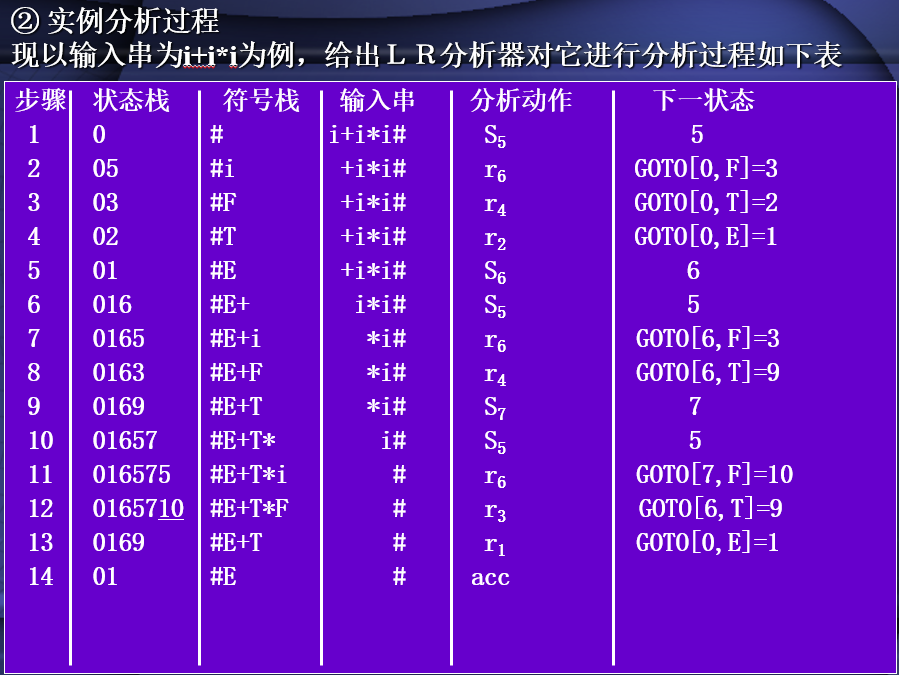
- 移进项目Sj:将j压入状态栈,并且将输入串首字符压入符号栈
- 归约项目rj:
- 根据j号规则替换符号栈的内容,然后根据j号规则右部有几个字符,则删去状态栈几个状态,
- 然后剩下的状态在查找此时符号栈对于的GOTO表,将查找的状态写入状态栈
- 接受项目acc:当符号栈只剩下开始符号,输入串没有字符,此时分析动作为acc,则表示分析成功。
LR(1)语法分析
只有以下两个部分与LR(0)不同:
- 在闭包扩展时,需要增加“,超前搜索符”,超前搜索符求解如下:
- 对于项目S′∷=·S,#,超前搜索符一定是#;
- 扩展的S∷=·a,#中的超前搜索符#,是求解S后面的所有(包括超前搜索符)的FIRST集
- 如果求解的FIRST集的非终结符号有多个,则超前搜索符也填写多个
- 归约项目填表时,只对ACTION表中,超前搜索符所在的列填写rj。
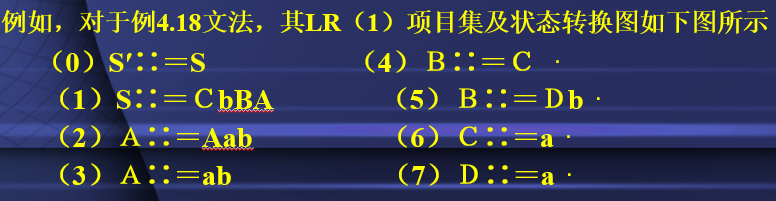

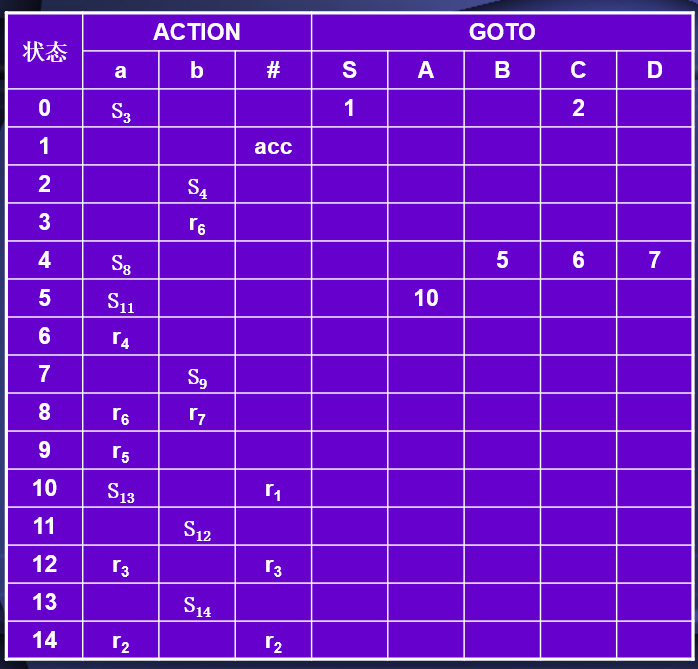
越努力越幸运!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号