第2章 形式语言基础知识

巴科斯范式(BNF)

• 第一次提出是为了描述ALGOL语言。
• 以“::=”符号(或“→”符号)表示定义为，以“|”符号表示或，以“〈〉”符号表示语法实体(语法单位)。

形式语言基本概念和术语

元语言

• 用来描述其他语言的语言称为元语言，被描述的语言是对象语言。
• 用尖括号括起来的词汇就是元语言变量或语法单位。

符号和符号串

字母表

• 有限个元素的非空集合称字母表，也称符号集。习惯上用V、Σ或其它大写字母表示。
• |V|表示字母表中符号的个数，符号是字母表中不再分解的最小单位。

符号串

• 符号串是字母表中的符号所组成的任何有穷序列，用t,u,v等小写字母表示。
• 空符号串ε，|ε|=0

行集合

• 字母表V上各种长度的符号串构成行集合，记为V^*，不包括空符号串的集合记为V⁺

关于行集合V^*上的几种运算

• 符号串联结：设有符号串x和y，则它们的联结xy是将符号串y直接拼接在符号串x之后。
• 行集合乘积：设A和B为两个符号串集合，并包含于V^*，则A和B的乘积定义为AB={xy|x∈A且y∈B}，满足x∈A且y∈B的所有符号串xy所组成的集合。
• 符号串的方幂：若x∈V^* ，是符号串。则x⁰=ε，x¹=x，x²=xx，x³=xxx，…xⁿ=xx…x(n个）。
• 行集合方幂：设符号串集合A∈V^*是行集合，则A⁰={ε}, A¹= A, A²= AA, A³= AAA, … Aⁿ = AAA…A (n个)。
• 行集合的闭包和正闭包:设A为符号串集合，则A的正闭包为A⁺=A¹∪A²∪…∪Aⁿ∪…；A的闭包为A^*=A⁰∪A⁺={ε}∪A⁺ （A+= AA* = A*A）。

产生式（规则）

• 产生式(规则)就是一个符号与另一个符号串的有序偶(U, x)，通常记为:U→x或U∷=x。
• 其中：U是符号，x是有限非空符号串。U称为规则的左部, x称为规则的右部
• 如果U→x₁|x₂|…|x_n,并称x_i是U的一个候选式。

字汇表V

• 用于规则左部和右部中所有符号形成集合为字汇表，记为V。
• 非终结符号：出现在规则左部，且能派生出符号或符号串的那些符号称为非终结符，也称语法实体或语法单位，它们的全体构成一个非终结符的集合，记为V_N
• 终结符号：规则中不属于V_N的那些符号称为终结符，它们的全体组成终结符的集合，记为V_T。
• V_N∪V_T=V，V_N∩V_T=Ø

文法G

• 文法是规则的有穷集合，形式定义为四元组：G=(V_N,V_T,P,Z)，文法G通常记为G[Z]。
• 其中：V_N是非终结符集合，V_T是终结符集合，P代表产生式集，Z∈V_N是文法G开始符号，也称识别符号，它至少要在一条产生式左部出现。

推导和归纳

• 直接推导/直接归约:v=>w，长度为1
• 推导/归约：v=>⁺w，长度≥1
• 广义推导/广义归约，v=>^*w，长度≥0

句型和句子

• 设G[Z]是一文法，若符号串x是由识别符Z推导而得，即Z=>*x，x∈V^*，则称符号串x为该文法G的一个句型。
• 如果一个句型x仅由终结符组成，即Z=>*x，x∈V_T^*，则称句型x为该文法的一个句子。
• 句子一定是句型，句型不一定是句子。

语言

• 设G[Z]为一文法，由该文法所产生的一切句子的集合称为由该文法所定义的语言，记为L(G[Z])(或L(G))，即L(G)={x|Z=>*x且x∈V_T*}

递归文法

• 在规则左部和右部具有相同的非终结符规则称为递归规则。非终结符U则成为递归非终结符。
• 如果一个语言是无穷的，则描述该语言的文法一定是递归文法。
• 对于一个文法，若有一个规则U∷=…U…，则称直接递归，若有规则U∷=U…，则称直接左递归，若有规则U∷=…U，则称直接右递归。
  
• 若有推导式U=>+…U…，则称间接递归，若有推导式U=>+U…，则称间接左递归，若有推导式U=>+…U，则称间接右递归。

短语和简单短语

短语和简单短语

设G[Z]是一文法，w=xuy是其中一句型

• 若有Z=>*xUy, U∈V_N且U=>+u,u∈V⁺,则称u是一个相对于非终结符U、句型w的短语。
• 若Z=>*xUy且U=>u,则称u是一个相对于非终结符U、句型w的简单短语。

1.短语或简单短语是由某非终结符推导得到的。
2.简单短语是由非终结符直接推导得到的，短语是由非终结符推导得到的，可见简单短语是短语的特例。
3.短语或者简单短语是句型w的子串
方法：在句型中的任一子串是否能由某非终结符推导得到

柄短语

• 一个句型最左边的简单短语称为该句型的句柄(或柄短语)，而且句柄最左边的符号称句柄的头，句柄最右边的符号称句柄的尾。

语法树

设有文法G=(V_N,V_T,P,Z)，满足下列条件的树即为一个语法树
a. 树中每一个结点都有标记，且该标记是V_N∪V_T中某一符号
b. 树根标记是识别符号
c. 若有一个结点至少有一个后继结点，则该结点标记必为非终结符
d. 若一个标记为U的结点，它有标记依次为X1，X2，X3，…，Xn的直接后继结点，则U∷=X1X2…Xn必定是G的一条规则。

• 树的末端结点标记从左到右连接起来就是要推导的句型或句子
• 末端结点的符号串是相对于子树根的短语，分支结点的符号串是相对于分支名字的简单短语(只有父子两代) ，最左简单子树的末端结点的符号串是句柄。

最左推导和最右推导

• 在任何一步推导v=>w中，都是对符号串v的最左(右)的非终结符进行替换，则称最左(右)推导。
• 规范推导：最右推导是规范推导，由规范推导所得的句型称为规范句型。如果推导v=>+w中每一步直接推导是规范的，则称推导v=>+w为规范推导。
• 规范归约：最右推导的逆过程称最左归约，最左归约也称为规范归约。
• 对于文法中的每一句子都必定有最左和最右推导，但对于一句型来说则不尽然。

文法二义性

• 如果一个文法中某个句型对应两棵不同的语法树，则称这个文法是二义性的。
• 也就是说，若一个文法中的某句型对应两个不同的最左推导或最右推导，则这个文法是二义性的。
• 一般只说文法二义性，而不说语言的二义性。

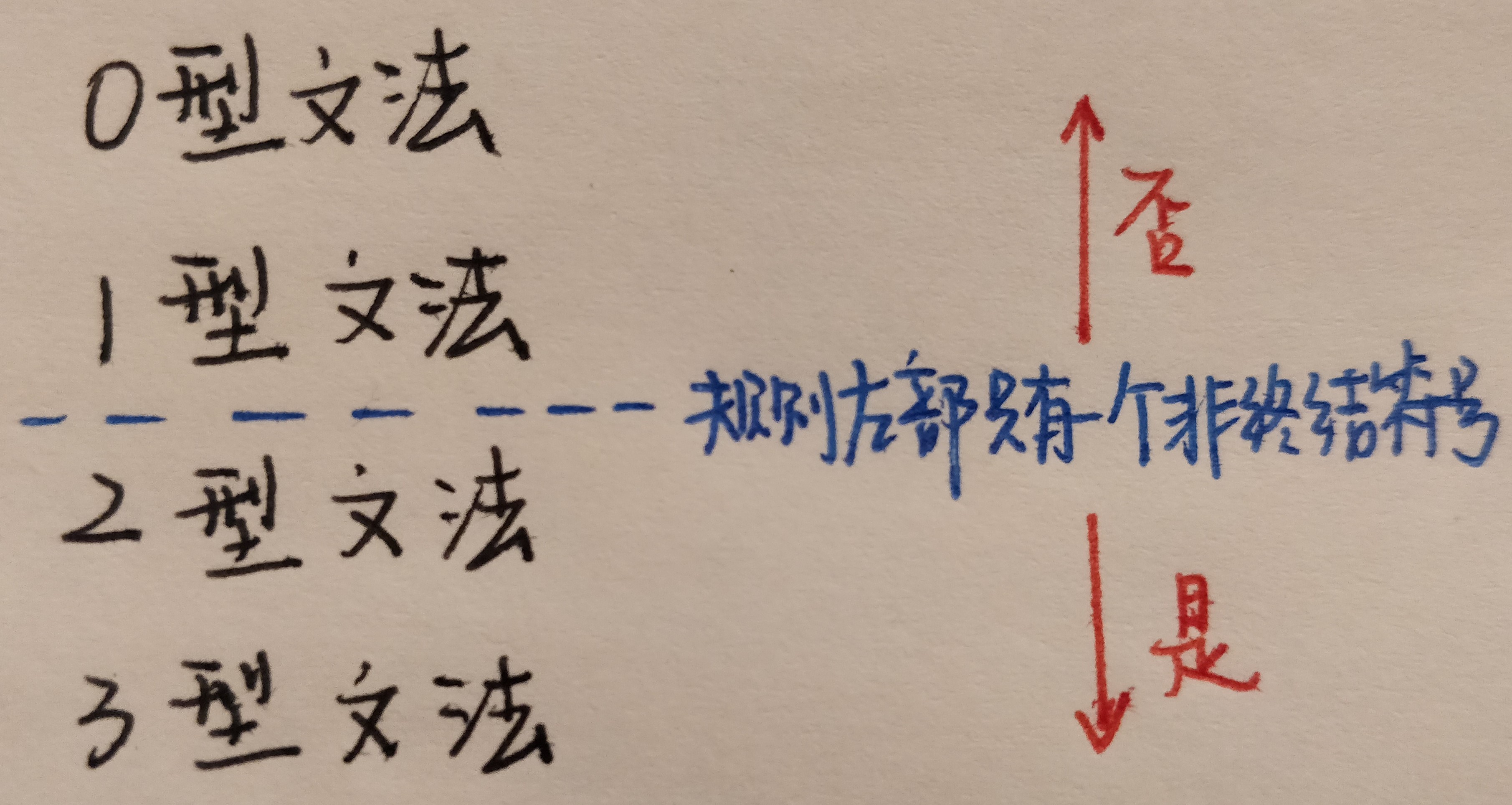
文法与语言分类

0型文法

• 若在文法G中，P中规则具有如下形式：α∷=β，其中α∈V+，且至少含一个非终结符，β∈Ｖ*
• 则文法G称为0型文法或称短语结构文法，由0型文法所描述和定义的语言称为0型语言,即L₀

1型文法

• 若在文法G中，P中规则具有如下形式：αAβ∷=αwβ其中α,β∈V*,A∈V_N,w∈V⁺
• 则称文法G为1型文法或上下文有关文法。1型文法相应的语言称1型语言，即L₁
• 产生式右部不得为空(仅仅S→ε例外，但S不得出现在产生式右部)

2型文法

• 若在文法G中，P中规则具有如下形式：A∷=w，其中A∈V_N，w∈V^*
• 则称文法G为2型文法或称上下文无关文法，由2型文法所确定的语言称2型语言，即L₂

3型文法

• 若在文法G中，P中规则具有如下形式：A∷=aB或A∷=a，其中A,B∈V_N,a∈V_T则称文法G为右线性文法。
• 类似地，如P中规则有如下形式：A∷=Ba或A∷=a，则称文法G为左线性文法。S::= ε不是正规文法。
• 把左线性文法和右线性文法称3型文法或正规文法，由3型文法所产生的语言称3型语言，即L₃。3型文法与词法分析密切相关。

L₀⊃L₁⊃L₂⊃L₃

文法和自动机

• 3型文法和有穷自动机
• 2型文法和下推自动机
• 1型文法和线性界限自动机
• 0型文法和图灵机

压缩过文法

1. 在文法中不含有形如A∷=A的规则；
2. 在文法中不包含多余规则：
   • 每一个非终结符号A(Z除外)必须在某句型中出现(否则为不可到达的)，即Z=>*αAβ，其中α,β∈V^*
   • 非终结符A必须推出终结符串t来(否则为不可终止的)，即A=>⁺t，t∈VT*
3. 某规则删除后，所有的连带规则也必须删除掉。

扩充巴科斯范式

花括号{}

1. {t}ⁿ_m表示符号串t可重复出现m次、m+1次、m+2次,…,直到n次
2. {t}ⁿ表示符号串t不出现或至多出现n次
3. {t}_m表示符号串t至少重复m次
4. {t}表示符号串t不出现或出现任意多次

方括号[]

• 方括号用来表示可供选择的符号串，即[t]=ε或t

圆括号()

• 引入圆括号以后，可以在规则中提取因子。设文法规则Z∷=AB|AC，可以表示成Z∷=A(B|C)