题解：【JROI-7】hibernal

题目链接

交互题，显然返回值为 \(1\) 时在所分的两个组中各一个，否则则在所分的同一个组中。

限制次数的题一般都从数据范围入手，可以发现最大范围 \(\log_21000 \approx 9\)，再看这个最大操作次数为 \(19\) 次，八成就是跑两遍相关的算法了。

考虑二进制拆分，首先将按照二进制每一位上分组，每次单独看一位，将这一位上是 \(0\) 的分在一组里面，是 \(1\) 的分在一组里面，如果不在同一组中则说明最终答案的两个下标在二进制这一位下不同，询问次数为 \(\log_2n\)。

由于两个不同的数他们的二进制位上必然有一位不同，我们随便选一个不同的位，然后分成两组二分答案。具体就是始终固定一组，然后找另一组中的答案：将要选出答案的那一组不断二分缩小范围，剩下的放入一组。大致就是下图这么一个过程。

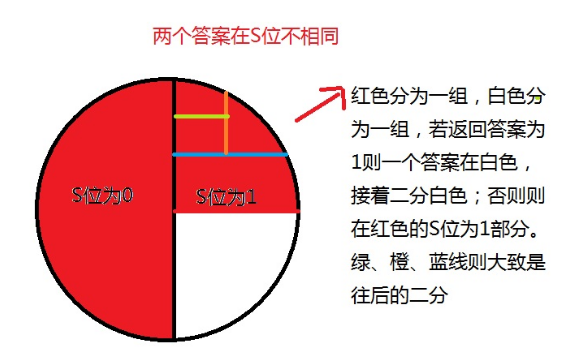
因为我们知道了两个答案在二进制位上哪一位相同哪一位不同，就可以直接推出另一个答案了。第一次的分组可以在前面的询问中记录下来一个，后面二分答案询问次数则是严格小于 \(\log_2n\) 的。

\(Code\)

#include<bits/stdc++.h>
#define int long long
using namespace std;

namespace LgxTpre
{
    static const int MAX=100010;
    static const int INF=200707070707;

    int T,n,g;
    bool check[20];
    int lis[MAX],l,r,t;

    inline void init()
    {
    	memset(check,0,sizeof check);
	memset(lis,0,sizeof lis);
	l=1,r=0;
    	cin>>n;
    	t=__lg(n);
    }

    inline void Binary_Split()
    {
        for(int k=0;k<=t;++k)
	{
		int cnt=0;
		cout<<"? ";
		for(int i=1;i<=n;++i)
			if(((i>>k)&1)==1) 
				++cnt;
		cout<<cnt<<" ";
		for(int i=1;i<=n;++i)
			if(((i>>k)&1)==1)
				cout<<i<<" ";
		cout<<endl;
		cin>>check[k];
		if(check[k]==1) g=k;
	}
    }
    inline void Binary_Group()
    {
        for(int i=1;i<=n;++i)
		if(((i>>g)&1)==1)
			lis[++r]=i;
	while(l<r)
	{
		int mid=(l+r)>>1,op,cnt=0;
		cout<<"? ";
		for(int i=l;i<=mid;++i)
			++cnt;
		cout<<cnt<<" ";
		for(int i=l;i<=mid;++i)
			cout<<lis[i]<<" ";
		cout<<endl;
        	cin>>op;
		if(op==0) l=mid+1;
		else r=mid;
	}
    }
    inline void Find_Answer()
    {
        int x=lis[l],y=x;
	for(int i=0;i<=t;++i)
		if(check[i])
			y=y^(1<<i);
	if(x>y) swap(x,y);
	cout<<"! "<<x<<" "<<y<<endl;
    }

    inline void lmy_forever()
    {
        ios::sync_with_stdio(false);
        cin.tie(0);
        cin>>T;
        while(T--)
        {
            init();
            Binary_Split();
            Binary_Group();
            Find_Answer();
        }
    }
}

signed main()
{
	LgxTpre::lmy_forever();
	return (0-0);
}