洛谷 P3272 [SCOI2011]地板 黑 题解

前言

做这道题前建议先把模板消化掉，见下行

这个题是插头 DP 的应用，相对于模板题来说变化还是挺大的。

初步分析

最大的区别莫过于它最后不是要求成环，不过动态规划嘛，就这德行……

我们依旧采用四进制来维护每一行的状态，并且每条已遍历和未遍历的分界线的数依旧是 \(x \in \{0,1,2\}\)，只不过对应的意义变了。

\(x=0\) 表示该边没有插头，\(x=1\) 表示该边有插头且所扑的地毯到目前为止没有拐弯，\(x=2\) 表示该边有插头且所扑的地毯到目前为止拐且只拐了一次弯。

那么问题就好解决了，只要细心想，转移方程就迎刃而解了。

用图像来解释状态转移方程

在放图之前，在这里我想列一个列表，希望能够清楚地呈现出各种情况。

令 \(x\) 表示某个方格左边插头状态，\(x\) 表示某个方格上边插头状态，

  1. \((i,j)\) 是障碍物，此时如果 \(x=0,\ y=0\)，那么可以加入新状态（和原状态一样，不用变化）；否则无解（显然），不用管它。
  2. \(x=0,\ y=0\) 有三种转移方程，详情见下图。
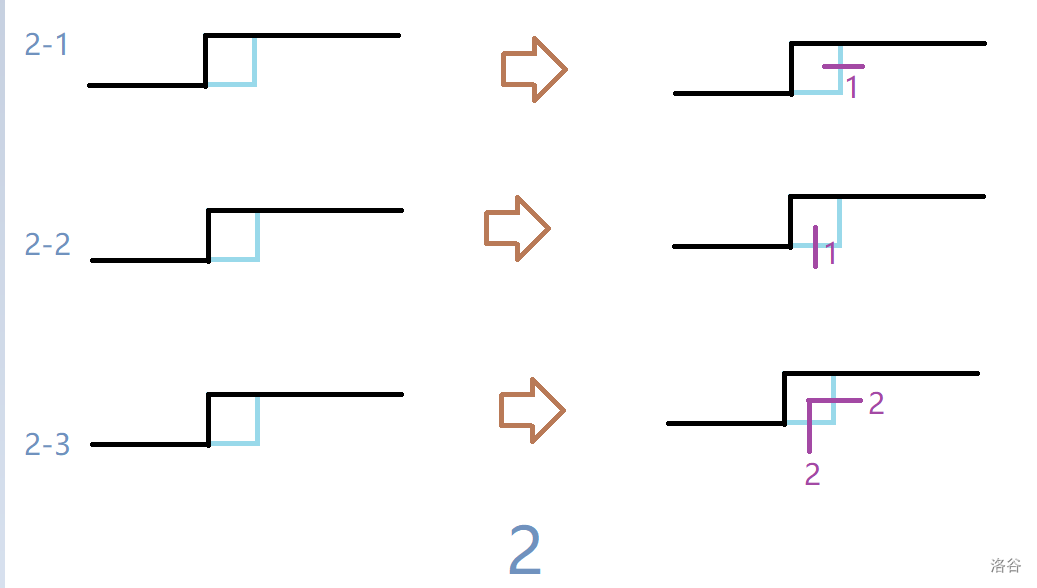
  3. \(x=0,\ y=1\) 有二种转移方程，详情见下图。
  4. \(x=1,\ y=0\) 有二种转移方程，详情见下图。
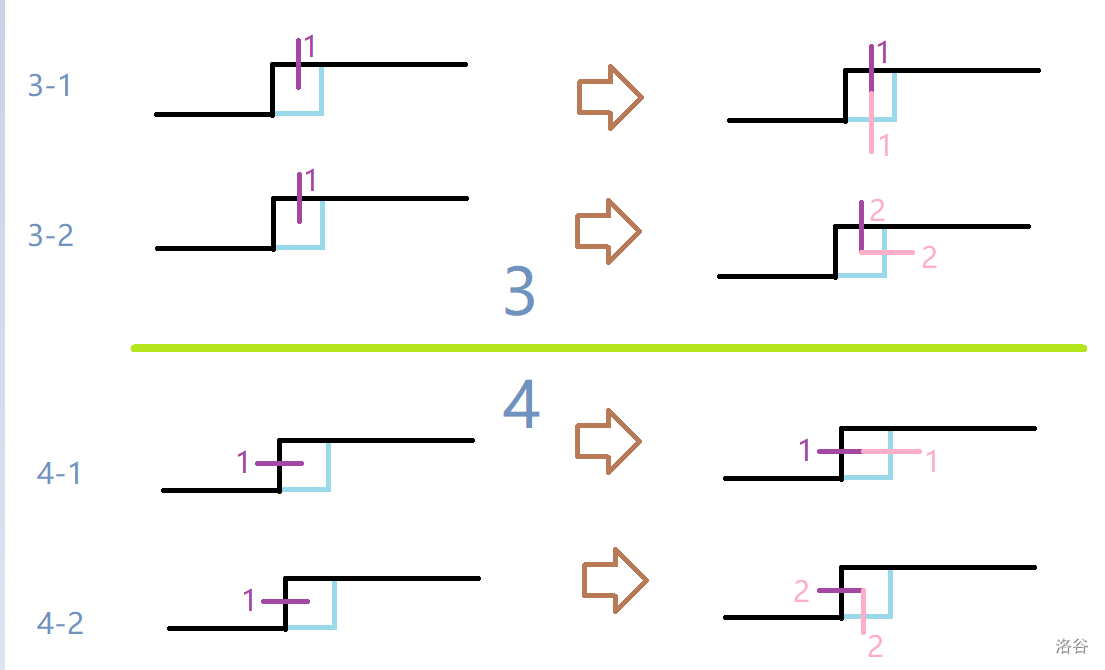
  5. \(x=0,\ y=2\) 有二种转移方程，详情见下图。
  6. \(x=2,\ y=0\) 有二种转移方程，详情见下图。
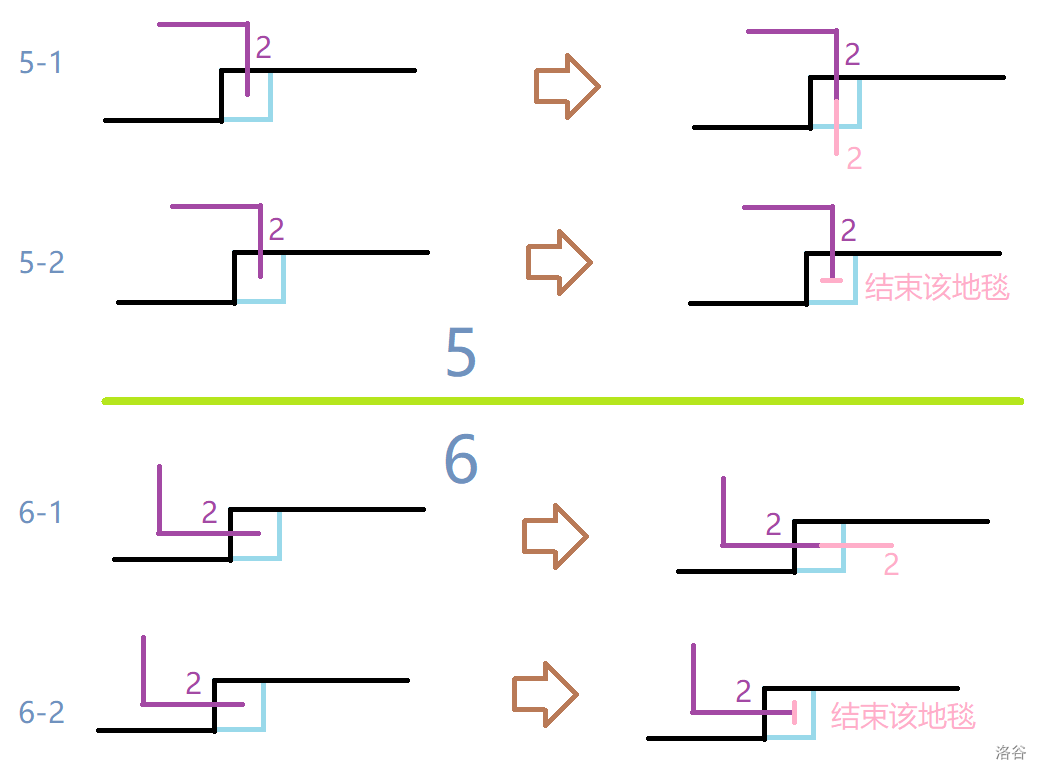
  7. \(x=1,\ y=1\) 在这里必须封口。为什么？如果不封口，那么 \(x,y\) 中必定有一个一次也没拐弯且前路已断，今生不可能再次被访问到，那么它就不符合要求。
  8. \(\begin{cases} x=1,\ y=2 \\ x=2,\ y=1 \\ x=2,\ y=2 \end{cases}\) 的情况是不可能出现的，因为这三种情况已将被前面几种情况覆盖了！（看了 @Orion545 大佬的题解才明白这一点）

那么接下来，对于第二到第六种情况……上图~

第二种

第三、四种

第五种、六种

细节/实现

手写哈希表可提高速度，用滚动数组省空间。

Code

#include <iostream>
#include <cstring>
#include <string>

using namespace std;

const int N = 180000, M = N * 2 + 7, mod = 20110520;

int n, m, end_x, end_y;
int maze[110][110], q[2][N], cnt[2];
int h[2][M], v[2][M];

int find_pos(int cur, int x)
{
	int t = x % M;
	while (h[cur][t] != -1 && h[cur][t] != x)
		if ( ++ t == M) t = 0;
	return t;
}

void add(int cur, int state, int w)
{
	int t = find_pos(cur, state);
	if (h[cur][t] == -1)
	{
		h[cur][t] = state;
		v[cur][t] = w;
		q[cur][ ++ cnt[cur]] = t;
	}
	else v[cur][t] = (v[cur][t] + w) % mod;
}

int get(int state, int k)
{
	return (state >> (k * 2)) & 3;
}

int stt(int k, int v)
{
	return v * (1 << (k * 2));
}

void rap()
{
	swap(n, m);
	swap(end_x, end_y);
	for (int i = 1; i <= n; i ++ )
		for (int j = 1; j < i; j ++ )
			swap(maze[i][j], maze[j][i]);
	return;
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	
	cin >> n >> m;
	for (int i = 1; i <= n; i ++ )
	{
		string s;
		cin >> s;
		s = ' ' + s;
		for (int j = 1; j <= m; j ++ )
			if (s[j] == '_')
			{
				maze[i][j] = 1;
				end_x = i;
				end_y = j;
			}
	}
	
	if (n < m) rap();
	
	int ans = 0;
	memset(h, -1, sizeof h);
	int cur = 0;
	add(cur, 0, 1);
	
	for (int i = 1; i <= n; i ++ )
	{
		for (int j = 1; j <= cnt[cur]; j ++ )
			h[cur][q[cur][j]] <<= 2;
		
		for (int j = 1; j <= m; j ++ )
		{
			int lst = cur;
			cur ^= 1;
			cnt[cur] = 0;
			memset(h[cur], -1, sizeof h[cur]);
			
			for (int k = 1; k <= cnt[lst]; k ++ )
			{
				int state = h[lst][q[lst][k]];
				int w = v[lst][q[lst][k]];
				int x = get(state, j - 1);
				int y = get(state, j);
				
				if (!maze[i][j])
				{
					if (!x && !y) add(cur, state, w);
				}
				else if (!x && !y)
				{
					if (maze[i][j + 1]) add(cur, state + stt(j, 1), w);
					if (maze[i + 1][j]) add(cur, state + stt(j - 1, 1), w);
					if (maze[i][j + 1] && maze[i + 1][j]) add(cur, state + stt(j, 2) + stt(j - 1, 2), w);
				}
				else if (!x && y == 1)
				{
					if (maze[i + 1][j]) add(cur, state - stt(j, y) + stt(j - 1, y), w);
					if (maze[i][j + 1]) add(cur, state + stt(j, 1), w);
				}
				else if (x == 1 && !y)
				{
					if (maze[i][j + 1]) add(cur, state - stt(j - 1, x) + stt(j, x), w);
					if (maze[i + 1][j]) add(cur, state + stt(j - 1, 1), w);
				}
				else if (!x && y == 2)
				{
					if (i == end_x && j == end_y) ans = (ans + w) % mod;
					else if (maze[i + 1][j]) add(cur, state - stt(j, y) + stt(j - 1, y), w);
					add(cur, state - stt(j, y), w);
				}
				else if (x == 2 && !y)
				{
					if (i == end_x && j == end_y) ans = (ans + w) % mod;
					else if (maze[i][j + 1]) add(cur, state - stt(j - 1, x) + stt(j, x), w);
					add(cur, state - stt(j - 1, x), w);
				}
				else if (x == 1 && y == 1)
				{
					if (i == end_x && j == end_y) ans = (ans + w) % mod;
					add(cur, state - stt(j - 1, x) - stt(j, y), w);
				}
			}
		}
	}
	
	cout << ans << endl;
	
	return 0;
}

后语

这代码我调了许久……

参考资料：AcWing 2644. 地板（算法进阶课）

完结撒花！

posted @ 2022-08-12 17:28  LittleMoMol  阅读(149)  评论(0)    收藏  举报
*/