洛谷 P1791 [国家集训队]人员雇佣 紫 题解

前言

大家都能看出来是一个最小割，在此主要阐述一下连边的正确性。

博客欢迎你，为你开天辟地

连边方式

1. 源点 \(S\) 向每个点（经理）\(i\)，连容量为 \(\sum\limits_{k=1}^n E_{i,k}\) 的边。
2. 每个点（经理）\(i\) 向汇点 \(T\)，连容量为 \(A_i\) 的边。
3. 每个点（经理）\(i\) 向其他点（经理）\(j\)，连容量为 \(2 E_{i, j}\) 的边。
4. 答案为 \(\sum\limits_{i=1}^n \sum\limits_{j=1}^n E(i,j) - \operatorname{dinic}\)。

理论基础

答案最大是多少？自然是所有 \(E\) 相加。

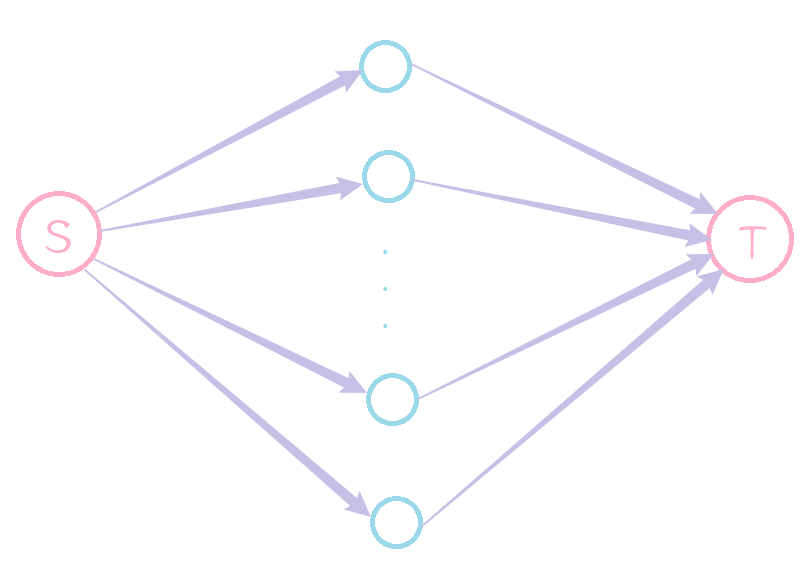
我们令连向 \(S\) 的点为雇佣者；连向 \(T\) 的点为不雇佣者。那么当答案最大时，图就长这样（当然，它不可能达到这个状态）。

这个图说明每个经理即雇佣了又没有雇佣，呈一种薛定谔的状态。

也就是说每个点我们只可以连 \(S\) 和 \(T\) 的其中一条边！

不考虑冲突，假如我们割去某个点与 \(T\) 的连边，说明我们要雇佣该经理，雇佣该经理就需要一些费用，而这些费用就该体现在这条边上，由此得知每个点连向 \(T\) 的边的容量为 \(A_i\)。

不考虑冲突，假如我们割去 \(S\) 与某个点的连边，说明我们要解雇该经理，解雇该经理就造成一定损失，而这些损失就该体现在这条边上，损失具体是多少？自然是所有第 \(i\) 行的 \(E\)，因为没了 \(i\) 这个经理，所有与 \(i\) 相关的价值都要被删去，由此得知 \(S\) 连向每个点的边的容量为 \(\sum\limits_{k=1}^n E_{i,k}\)。

考虑冲突，为什么要那样连边？先上图！

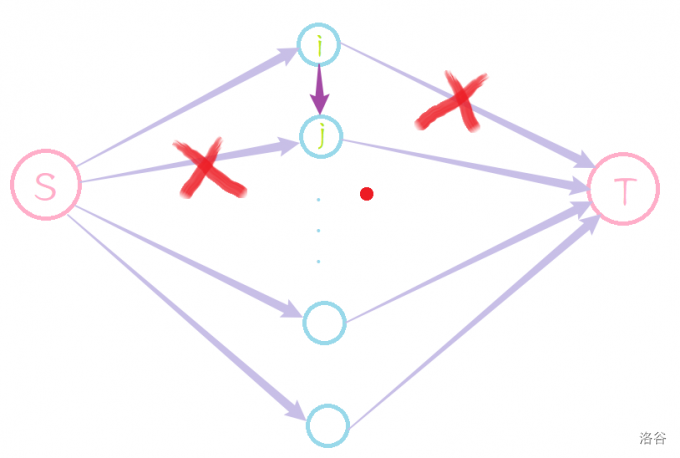
这个图的情况是选 \(i\) 但是不选 \(j\)。

首先如果两个点都连接于 \(S\) 或者 \(T\) ，那么中间的边是不起作用的，因为你们都在一个团队里了还互相残杀就说不过去了。

当 \(i\) 在 \(S\) 中，\(j\) 在 \(T\) 中，对于 \(i\) 他是对所在团队有 \(\sum\limits_{k=1}^n E_{i,k}\) 的贡献，但是！但是！ \(j\) 和 \(i\) 认识，因为 \(j\) 知道 \(i\) 的底细，所以 \(i\) 对团队做出的贡献中 \(E_{i,j}\) 白搭了！不仅白搭！还会减少 \(E_{i,j}\)！惊不惊喜？意不意外？，所以团队总贡献一下子少了 \(2 E_{i,j}\)，那么连的边的权值自然为 \(2E_{i,j}\)。

这告诉我们一个真理：不要把自己完全裸露在对方的视野里，要留一手备长局，步入社会后就是这样。

所以说跑一边最大流求最小割，用总价值减去它即可。

Code

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1010 * 1010, M = 2 * (N * 3);
const int INF = 0x3f3f3f3f;

int n, S, T, sum;
int maze[1010][1010];
int h[N], e[M], f[M], ne[M], idx;
int q[N], cur[N], depth[N];

int read()
{
	int s = 0, w = 1;
	char c = getchar();
	while (c < '0' || c > '9')
	{
		if (c == '-') w = -1;
		c = getchar();
	}
	while (c >= '0' && c <= '9')
	{
		s = s * 10 + c - '0';
		c = getchar();
	}
	
	return s * w;
}

void add(int a, int b, int c)
{
	e[idx] = b;
	f[idx] = c;
	ne[idx] = h[a];
	h[a] = idx ++ ;
	
	e[idx] = a;
	f[idx] = 0;
	ne[idx] = h[b];
	h[b] = idx ++ ;
	
	return;
}

bool bfs()
{
	int hh = 0, tt = 0;
	memset(depth, -1, sizeof depth);
	q[0] = S;
	depth[S] = 0;
	cur[S] = h[S];
	
	while (hh <= tt)
	{
		int t = q[hh ++ ];
		for (int i = h[t]; ~i; i = ne[i])
		{
			int ver = e[i];
			if (depth[ver] == -1 && f[i] > 0)
			{
				depth[ver] = depth[t] + 1;
				cur[ver] = h[ver];
				q[ ++ tt] = ver;
				if (ver == T) return true;
			}
		}
	}
	
	return false;
}

int dfs(int u, int lmt)
{
	if (u == T) return lmt;
	int flow = 0;
	for (int i = cur[u]; ~i && flow < lmt; i = ne[i])
	{
		cur[u] = i;
		int ver = e[i];
		if (depth[ver] == depth[u] + 1 && f[i] > 0)
		{
			int t = dfs(ver, min(f[i], lmt - flow));
			if (!t) depth[ver] = -1;
			f[i] -= t;
			f[i ^ 1] += t;
			flow += t;
		}
	}
	
	return flow;
}

int dinic()
{
	int res = 0, flow = 0;
	while (bfs())
		while (flow = dfs(S, INF))
			res += flow;
	return res;
}

int main()
{
	n = read();
	S = 0, T = n + 1;
	memset(h, -1, sizeof h);
	for (int i = 1; i <= n; i ++ )
	{
		int a = read();
		add(i, T, a);
	}
	for (int i = 1; i <= n; i ++ )
	{
		int tot = 0;
		for (int j = 1; j <= n; j ++ )
		{
			cin >> maze[i][j];
			sum += maze[i][j];
			tot += maze[i][j];
		}
		add(S, i, tot);
	}
	
	for (int i = 1; i <= n; i ++ )
		for (int j = 1; j <= n; j ++ )
		{
			if (i == j) continue;
			add(i, j, 2 * maze[i][j]);
		}
	
	cout << sum - dinic() << endl;
	
	return 0;
}

后语

思考是好的，完结撒花！