UVA1389 Hard Life 题解
UVA1389 Hard Life 题解
前言
由于这道题的建模很简单,所以在这里我们重点讨论一下最大密度子图的模板原理
问题描述
最大密度子图是这样一类问题:
给定一张图,选择其中的一个子图,使得该子图的点数除以边数的值最大。选择的子图必须满足:若一条边被选上,则其两个端点必须选;若一个点被选上,与其相邻的边可以不选,不做要求。(这个很好理解,图越密的话边数越多)
原图记为 \(G<V,E>\),子图记为 \(G'(V',E')\),子图中边的个数记为 \(|E'|\),子图中点的个数记为 \(|V'|\),我们要求的是 \(\max\left(\dfrac{|E'|}{|V'|}\right)\)
总框架
对于分数的最值,通常会用 01 分数规划来解决,而对于 01 分数规划问题,通常用二分来解决。
那么我们可以二分枚举 \(g\),若 \(\max\left(\dfrac{|E'|}{|V'|}\right) > g\),由于 \(|V'| \not= 0\),则有
反之,同理。
接下来考虑左边界和右边界,对于左边界,由于都是正数运算,故 \(L>0\);对于右边界,最极端的情况就是 \(1\) 个点连着 \(m\) 条边,所以 \(R \le m\)。
对于每个 \(g\),我们最渴望解决的就是求出 \(|E'|-g|V'|\) 的值。
重点:求值
设想一下,如果某个子图已经确定了,也就是 \(|V'|\) 固定,那么要使 \(\dfrac{|E'|}{|V'|}\) 最大,只需让 \(|E'|\) 最大,那最优情况一定是点集的诱导子图。
诱导子图:选出来的子图,满足点与点的连边都在子图中,形式化地,对于子图 \(G'<V',E'>\) 中的所有的 \(u, v\) 都有 \((u, v) \in E'\) 。
接着,要将诱导子图的边一个个找出来。
正难则反,可以用所选点的度数-所选点集的补集与这个点集所连的边来求出。
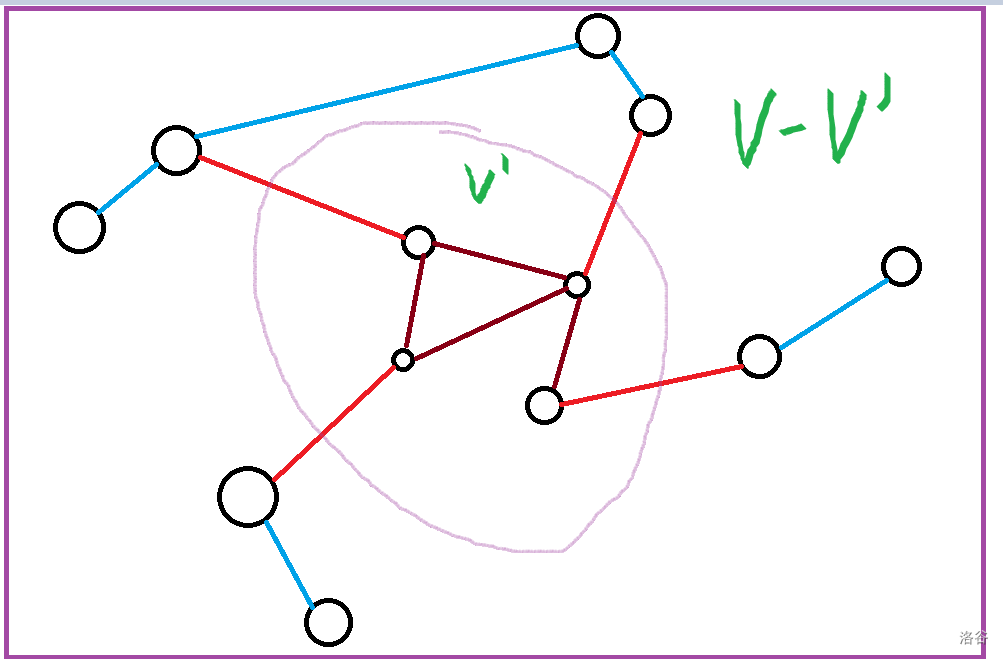
在这个图中,若选择的子图为 \(V'\),红色的边即为“所选点集的补集与这个点集所连的边”
统计所选点的度数很简单,但后者就不易了,如上图,对于红色的边,它像什么?它是不是非常像最小割!对叭~那么就来考虑最小割!
因为是最小割,我们就把最大化 \(|E'| - g|V'|\) 的问题转化为最小化 \(g|V'|-|E'|\) 的问题。
接下来,我们看一看 \(g|V'|-|E'|\) 究竟是啥
令 \(d_v\) 为点 \(v\) 的度数,\(C(S,T)\) 为集合 \(S\) 和 \(T\) 最小割,那么
我们想让原问题和最小割一一对应起来,但不幸的是,除了最小割,还多了一项让人讨厌的 \(\sum \limits_{v \in V'} (2g - d_v)\),我们想如何可以把它“集合”到最小割里面。
我们可以这样做
- 将所有 \(v \in V\) 向汇点 \(T\) 连一条权值为 \(2g-d_v+U\) 的边( \(U\) 为常数,来确保权值非负)
- 若 \(u,v,e_{u,v} \in G\) ,则 \(u\) 向 \(v\) 连一条容量为 \(1\) 的边
- 源点 \(S\) 向 \(u \in V\) 连一条容量为 \(U\) 的边
为什么这样建图?暂且不管。建完后,我们看一看 \(C(S,T)\) 究竟是什么
令 \(V'=S-\{s\},\enspace \overline{V'}=V-V'\),则有
因为 \(Un\) 是一个常数,所以 \(g|V'|-e|E'|\) 与 \(C(S,T)\) 的大小是有线性关系的。
这也正是这样建图的妙处,一一对应上了!
最终,我们得到了
好耶!接下来就是敲代码啦!
Code
#include <iostream>
#include <cstring>
using namespace std;
const int N = 110, M = (1000 + N * 2) * 2, INF = 1e8;
int n, m, S, T;
int h[N], e[M], ne[M], idx;
double f[M];
int q[N], depth[N], cur[N];
int dg[N];
struct warma
{
int a, b;
} edges[M];
int ans;
bool st[N];
void add(int a, int b, double c1, double c2)
{
e[idx] = b;
f[idx] = c1;
ne[idx] = h[a];
h[a] = idx ++ ;
e[idx] = a;
f[idx] = c2;
ne[idx] = h[b];
h[b] = idx ++ ;
return;
}
void build(double g)
{
memset(h, -1, sizeof h);
idx = 0;
for (int i = 0; i < m; i ++ )
add(edges[i].a, edges[i].b, 1, 1);
int U = m;
for (int i = 1; i <= n; i ++ )
{
add(S, i, U, 0);
add(i, T, U + 2 * g - dg[i], 0);
}
}
bool bfs()
{
int hh = 0, tt = 0;
memset(depth, -1, sizeof depth);
q[0] = S;
depth[S] = 0;
cur[S] = h[S];
while (hh <= tt)
{
int t = q[hh ++ ];
for (int i = h[t]; ~i; i = ne[i])
{
int ver = e[i];
if (depth[ver] == -1 && f[i] > 0)
{
depth[ver] = depth[t] + 1;
cur[ver] = h[ver];
q[ ++ tt] = ver;
if (ver == T) return true;
}
}
}
return false;
}
double dfs(int u, double lmt)
{
if (u == T) return lmt;
double flow = 0;
for (int i = cur[u]; ~i; i = ne[i])
{
cur[u] = i;
int ver = e[i];
if (depth[ver] == depth[u] + 1 && f[i] > 0)
{
double t = dfs(ver, min(f[i], lmt - flow));
if (t <= 0) depth[ver] = -1;
f[i] -= t;
f[i ^ 1] += t;
flow += t;
}
}
return flow;
}
double dinic(double g)
{
build(g);
double res = 0, flow = 0;
while (bfs())
while (flow = dfs(S, INF))
res += flow;
return res;
}
void way(int u)
{
st[u] = true;
if (u != S) ans ++ ;
for (int i = h[u]; ~i; i = ne[i])
{
int ver = e[i];
if (!st[ver] && f[i] > 0)
way(ver);
}
return;
}
int main()
{
while (cin >> n >> m)
{
//cin >> n >> m;
S = 0, T = n + 1;
memset(dg, 0, sizeof dg);
memset(st, 0, sizeof st);
ans = 0;
for (int i = 0; i < m; i ++ )
{
int a, b;
cin >> a >> b;
dg[a] ++ ;
dg[b] ++ ;
edges[i] = {a, b};
}
double L = 0, R = m;
int U = m;
while (R - L > 1e-8)
{
double mid = (L + R) / 2;
double t = dinic(mid);
if (U * n - t > 0) L = mid;
else R = mid;
}
dinic(L);
way(S);
if (!ans) cout << 1 << endl << 1 << endl;
else
{
cout << ans << endl;
for (int i = 1; i <= n; i ++ )
if (st[i])
cout << i << endl;
}
cout << endl;
}
return 0;
}
后语
写这篇题解前我还是不太理解最大密度子图的蒟蒻,而写题解的过程中通过看论文、视频等等方式,肝了一夜,终于完成了题解并大致理解了!希望大家也多多通过这种方式学习,真的很有效果呢~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号