洛谷 P5752 [NOI1999] 棋盘分割 题解

P5752 [NOI1999] 棋盘分割

前言

看大部分题解里面都是多层循环，看着太壮观啦！我来提供一个不需要循环的方法，用记忆化搜索！

什么？数学公式不会推？这篇题解的方法，根本不用推数学公式！

思路

要使 \(\sqrt{\dfrac{\sum\limits_{i=1}^{n}(x_1-\overline{x})^2}{n}}\) 最小，也就是使 \(\dfrac{\sum\limits_{i=1}^{n}(x_1-\overline{x})^2}{n}\) 最小，考虑怎么快速计算 \(\overline{x}\)，很显然，可以用二维前缀和计算。

我们令 \(f[x_1][y_1][x_2][y_2][k]\) 表示在左上角坐标为 \((x_1,y_1)\) 右下角坐标为 \((x_2,y_2)\) 的矩形中切 \(k-1\) 刀分割成了 \(k\) 个小矩形后所得的均方差的最小值，那么答案就为 \(f[1][1][8][8][n]\)。

考虑状态转移方程，由于刀可以横切也可以竖切，而对于横切或者竖切，又有取那一块的选择，所以有四种情况，分别对应下图的甲乙丙丁。

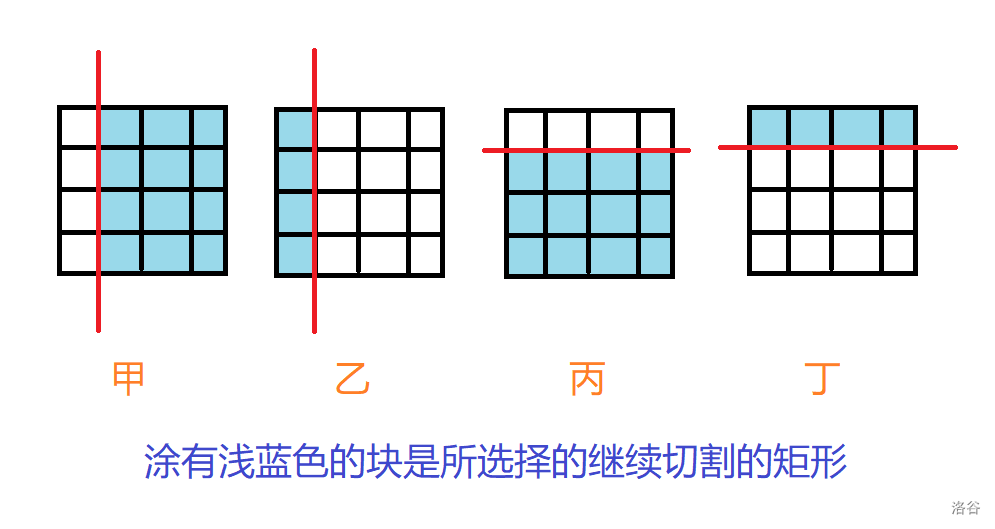
那么状态转移方程就可以得到了，详见代码注释。

代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>

using namespace std;

const int N = 15, M = 9;
const double INF = 1e9;

int n, m = 8;
int s[M][M];
double f[M][M][M][M][N];
double X;

//求块内均方差
double get(int x1, int y1, int x2, int y2)
{
	double sum = s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] - X;
	return sum * sum / n;
}

//重点：记忆化搜索
double dp(int x1, int y1, int x2, int y2, int k)
{
	double &v = f[x1][y1][x2][y2][k];
	if (v >= 0) return v;
	if (k == 1) return v = get(x1, y1, x2, y2);
	
    //状态转移方程 始
	v = INF;
	for (int i = x1; i < x2; i ++ ) //枚举纵向切的位置
	{
		v = min(v, dp(x1, y1, i, y2, k - 1) + get(i + 1, y1, x2, y2));//对应图乙
		v = min(v, dp(i + 1, y1, x2, y2, k - 1) + get(x1, y1, i, y2));//对应图甲
	}
	for (int i = y1; i < y2; i ++ ) //枚举横向切的位置
	{
		v = min(v, dp(x1, y1, x2, i, k - 1) + get(x1, i + 1, x2, y2));//对应图丁
		v = min(v, dp(x1, i + 1, x2, y2, k - 1) + get(x1, y1, x2, i));//对应图丙
	}
    //状态转移方程 收
	
	return v;
}

int main()
{
	cin >> n;
    //求二维前缀和
	for (int i = 1; i <= m; i ++ )
		for (int j = 1; j <= m; j ++ )
		{
			cin >> s[i][j];
			s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
		}
	
	memset(f, -1, sizeof f);
	X = (double) s[m][m] / n; //平均数
	
	printf("%.3lf\n", sqrt(dp(1, 1, 8, 8, n)));
	
	return 0;
}