洛谷 P3422 [POI2005]LOT-A Journey to Mars 题解

P3422 [POI2005]LOT-A Journey to Mars 题解

前言

了解过单调队列嘛？如果还没有的话，建议做完 P1886 滑动窗口 /【模板】单调队列 再做此题。

思路

No. 1 破环成链

首先题目给的是环，自然要破环成链，我最喜欢的一种方式是，复制一份，如下图。

淡黄色为每次遍历经过的点，可以发现，和环形的遍历是等价的。

No. 2 怎么想到用单调队列的？

\(p_i\) 存下第 \(i\) 个加油站的油量，\(d_i\) 表示第 \(i\) 个加油站和第 \((i+1) \operatorname{mod}\ n\) 个加油站的距离（模 \(n\) 的原因是最后一个加油站和第一个加油站是相邻的），以下图为例：

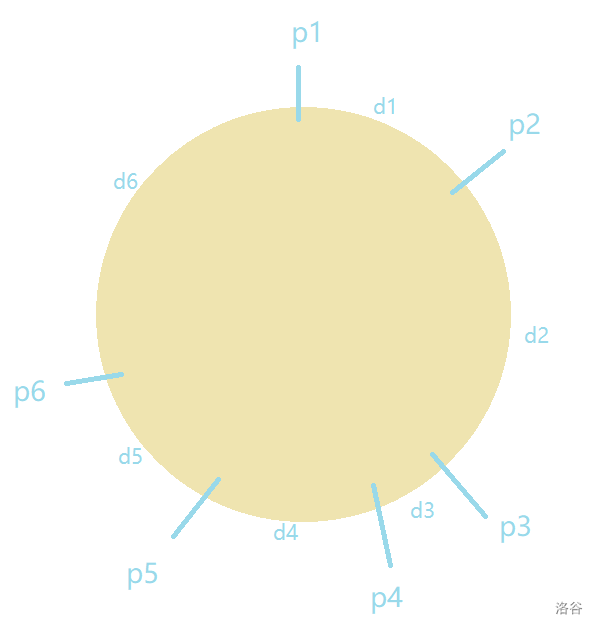
下面展示分析问题的过程

• 先以顺时针为例，如果想要转完一圈，就必须保证每一步都可以到达下一个加油站，比如：想要从第一个加油站走到第二个加油站，就必须满足 \(p_1 - d_1 \ge 0\)，类似地，想要从第一个加油站走到第三个加油站，就必须满足 \(p_1 - d_1 \ge 0\) 且 \(p_1 + p_2 - d_1 - d_2 \ge 0\)，可知如果想走完一圈，也就是从第一个加油站走到第 \(n\) 个加油站，就必须满足 \(\forall\ k \in [1,n],\ \sum\limits _{i=1}^{k}p_i - \sum\limits _{i=1}^{k}t_i \ge 0\)

• 那么如何快速求出式子呢，你一定最先想到前缀和，那么我们令 \(s_i\) 表示 \(\sum\limits _{j=1}^{i}p_j - \sum\limits _{j=1}^{i}t_j\)。那么对于第 \(i\) 个加油站，只需要满足 \(\forall\ k \in [i,i + n],\ s_k - s_{i-1} \ge 0\)。

• 你会发现每一个前缀和都要判断，有没有一种方法，使得只用判断一次呢？可以发现，只需要让所有的 \(s_k\) 中最小的那个满足 \(s_k - s_{i-1} \ge 0\) 即可。

• 也就是说，当前最大的问题是如何快速找到最小的 \(s_k\)，于是就很自然地想到了单调队列，用一个单调队列维护前缀和的最小值。

No. 3 细节多

顺时针	逆时针
维护该点往后的 \(n\) 个点的前缀和，所以要从后往前遍历	维护该点往前的 \(n\) 个点的前缀和，所以要从前往后遍历
\(s_i = p_i - d_i\)	\(s_i = p_i - d_{i-1},\ d_0 = d_n\)
维护 \(s_k\) 的最小值（原因见后文）	维护 \(s_k\) 的最大值（原因见后文）
先出队再更新	先更新再出队
当遍历到 \(i \le n\) 的加油站再更新答案	当遍历到 \(i > n\) 的加油站再更新答案

对于第三条，放一个图，就能明白了

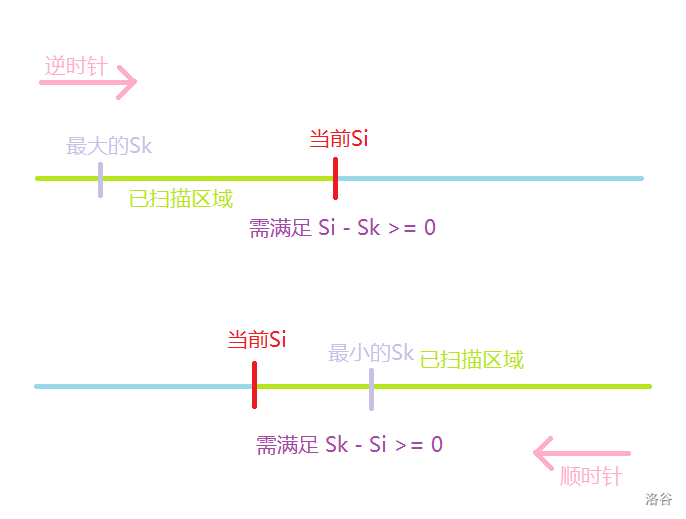
Code

#include <cstring>
#include <iostream>

using namespace std;

typedef long long LL;

const int N = 2e6 + 10;

int n;
int p[N], d[N];
LL s[N];
int q[N];
bool ans[N];

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	
	cin >> n;
	for (int i = 1; i <= n; i ++ ) cin >> p[i] >> d[i];
	
	//顺时针
	for (int i = 1; i <= n; i ++ )
		s[i] = s[i + n] = p[i] - d[i]; //对应细节2
	for (int i = 1; i <= n * 2; i ++ )
		s[i] += s[i - 1];
	
	int hh = 0, tt = -1;
	for (int i = n * 2; i; i -- ) //对应细节1
	{
		if (hh <= tt && q[hh] >= i + n) hh ++ ;
		while (hh <= tt && s[q[tt]] >= s[i]) tt -- ; //对应细节3，细节4
		q[ ++ tt] = i;
		if (i <= n)  //对应细节5
		{
			if (s[q[hh]] - s[i - 1] >= 0) ans[i] = true;
		}
	}
	
	//逆时针
	d[0] = d[n];  //对应细节2
	for (int i = 1; i <= n; i ++ )
		s[i] = s[i + n] = p[i] - d[i - 1]; //对应细节2
	for (int i = 1; i <= n * 2; i ++ )
		s[i] += s[i - 1];
	
	hh = 0, tt = -1;
	for (int i = 1; i <= n * 2; i ++ ) //对应细节1
	{
		if (hh <= tt && q[hh] < i - n) hh ++ ;
		if (i > n)  //对应细节5
		{
			if (s[i] - s[q[hh]] >= 0) ans[i - n] = true;
		}
		while (hh <= tt && s[q[tt]] <= s[i]) tt -- ; //对应细节3，细节4
		q[ ++ tt] = i;
	}
	
	for (int i = 1; i <= n; i ++ )
		if (ans[i]) cout << "TAK" << endl;
		else cout << "NIE" << endl;
	
	return 0;
}

后语

我在写这篇题解的时候有一个小插曲，让我 debug 了好长时间，在此分享一下

错误的写法

while (hh <= tt && s[q[tt] <= s[i]]) tt -- ;

正确的写法

while (hh <= tt && s[q[tt]] <= s[i]) tt -- ;

可太难调了捏~

制作不易，盼君一赞。

完结撒花！！