洛谷 CF442C Artem and Array 紫 题解

前言

说实话这道题确实不太适合作为紫题，但是它的思路很妙，在此我详细解释一下每一步操作背后的原因。

大致流程

1. 从前往后读入数组 \(a\)，对于一个下标 \(pos\)，若其满足 \(a[pos-1] \ge a[pos]\) 且 \(a[pos] \le a[pos+1]\)，那么将答案 \(ans+= \min(a[pos-1],\ a[pos+1])\)，并删除 \(a[pos]\)。
2. 将 \(a\) 数组中剩余数按从小到大排序，若 \(a\) 数组中还剩下 \(n\) 个数，那么让 \(ans\) 再加上 \(a\) 的前 \(n-2\) 项即为答案。

理论基础

对于第一步

为什么要找“V”型？

我们令 \(a[pos-1] \ge a[pos]\) 且 \(a[pos] \le a[pos+1]\)，那么如果我们不删除 \(a[pos]\) 而去删除 \(a[pos-1]\) 或 \(a[pos-1]\)，那么得到的价值最大也只能是 \(a[pos]\)；然而若删除 \(a[pos]\)，那么得到的价值为 \(\min(a[pos-1], a[pos+1])\)，由于 \(a[pos-1]\) 和 \(a[pos+1]\) 必然都是大于等于 \(a[pos]\) 的，所以删除 \(a[pos]\) 更优。

为什么见到一个“V”型就可以直接删除？

这个困扰了我许久，最终找到了答案。我们令“V”型三元组为 \((x,y,z)\)，其中 \(a[x] \ge a[y],\ a[y] \le a[z]\)，那么可以发现任意两个“V”型三元组的 \(y\) 不可能相邻（除了这两个 \(y\) 相等）。

如果 \(y\) 不相等，那么每一个“V”型是互不影响的，所以你先删哪个后删哪个效果是一样的。

如果 \(y\) 相等，比如 \((x,\ y,\ y,\ y,\ z)\)，容易发现你先删哪一个 \(y\) 所获得的价值是一样的，都是 \(a[y]\)，那么顺序仍然不影响结果。

注意：每一次删除可能不止删一个 \(y\)

对于第二步

单峰

你会发现剩下的 \(a\) 数组中是没有“V”型的，这很显然。进一步地，它还是单峰的，如果说大白话，那就是“它下去了就上不来了”，因为如果下去再上来，那么拐点处和其左右相邻的点构成一个“V”型，这就矛盾了！

不可能取到 \(a\) 中的最大值和次大值

最大值肯定去不到，因为有次大值拖着后退呢~

次大值也取不到，为什么？反证法！如果可以取到次大值，那么必然存在一个下标 \(pos\) 使得 \(a[pos]\) 在最大值和次大值中间，那它们岂不是构成了“V”型？！矛盾！！

能否将最大值和次大值之外的所有值都取一遍？

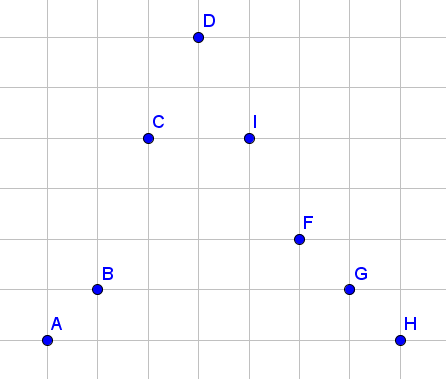
先举一个例子，直接上图！

（纵坐标即为对应值的大小）

删 \(D\) 取 \(C\)
删 \(C\) 取 \(B\)
删 \(I\) 取 \(F\)
删 \(F\) 取 \(G\)
删 \(G\) 取 \(H\)
删 \(B\) 取 \(A\)
最后删 \(A,H\)

大致方法就是永远删最上面的，即可保证。严格证明我也不会，感性理解叭。

为什么最优解是将除了最大值和次大值之外的所有值都取一遍？

因为只能取除了最大值和次大值之外的值，所以我们只需证明，重复取同一个值只会使答案更劣。

对于一个下标 \(pos\) 以及其对应的值 \(a[pos]\)，每一次删数操作，如果所删的数小于 \(a[pos]\)，那么这个操作对答案的贡献不可能是 \(a[pos]\)，这种情况就无需讨论了。

如果所删的数大于等于 \(a[pos]\)，那么 \(a[pos]\) 是可以作为答案的贡献的。我们考虑如果删了两个数，对答案的贡献均为 \(a[pos]\)，那么这两个数必然是相邻的，而如果所删的两个数是相邻的，那么我们可以将这两个数删去的顺序换一下，答案一定不会变差，举个具体例子。

比如上面那张图，我们先删 \(I\)，再删 \(D\)，这两次操作的贡献都是 \(F\) 对应的值；而如果我们先删 \(D\)，再删 \(I\)，贡献则为 \(I+F\)，更优。

Code

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 5e5, INF = 0x3f3f3f3f;

int n, m;
int a[N];
LL ans;

int read()
{
	int s = 0, w = 1;
	char c = getchar();
	while (c < '0' && c > '9')
	{
		if (c == '-') w = -1;
		c = getchar();
	}
	while (c >= '0' && c <= '9')
	{
		s = s * 10 + c - '0';
		c = getchar();
	}
	
	return s * w;
}

int main()
{
	n = read();
	a[1] = read(), a[2] = read();
	
	if (n == 1)
	{
		cout << 0 << endl;
		return 0;
	}
	
	for (int i = 3; i <= n; i ++ )
	{
		cin >> a[i];
		while (a[i - 2] >= a[i - 1] && a[i - 1] <= a[i] && i >= 2)
		{
			ans += min(a[i - 2], a[i]);
			a[i - 1] = a[i];
			n -- ;
			i -- ;
		}
	}
	
	sort(a + 1, a + 1 + n);
	for (int i = 1; i <= n - 2; i ++ ) ans += a[i];
	
	cout << ans << endl;
	
	return 0;
}

后语

我自己曾经说过：“严谨的证明是好的，囫囵吞枣只去追求刷题量是可耻的。”（尽管我也经常囫囵吞枣）

反正是终于整完了！肝了好久，盼君一赞~

完结撒花！