从损失函数优化角度：讨论“线性回归（linear regression）”与”线性分类（linear classification）“的联系与区别

1. 主要观点

线性模型是线性回归和线性分类的基础
线性回归和线性分类模型的差异主要在于损失函数形式上，我们可以将其看做是线性模型在多维空间中“不同方向”和“不同位置”的两种表现形式
损失函数是一种优化技术的具体载体，影响损失函数不同形式的因素主要有：
- 和谁比：和什么目标比较损失
- 怎么比：损失比较的具体度量方式和量纲是什么
- 比之后如何修正参数：如果将损失以一种适当的形式反馈给原线性模型上，以修正线性模式参数

在这篇文章中，笔者会先分别介绍线性回归（linear regression）和线性分类（linear classification）各自的定义和应用场景。然后用函数优化这个统一视角，将它们二者统一起来讨论，揭示它们二者的共性和区别。

2. 线性模型，线性回归和线性分类的基础

0x1：线性模型中的“线性”指的是什么

线性（linear），指量与量之间按比例、成直线的关系，在数学上可以理解为一阶导数为常数的函数，如下式：

Y = a₁x₁ + a₂x₂ + ..... + a_nx_n

这里Y和a_n，x可以是任何实值。

在二维平面上，线性函数就表现为一个直线：

在更高维的空间上，线性函数就是一个高维超平面。

与此相对的另一个概念，非线性（non-linear）则指不按比例、不成直线的关系，一阶导数不为常数。

在二维平面上，非线性函数就变现为一个曲线：

在更高维的空间上，非线性函数就是一个高维超曲面。

线性模式是很多复杂机器学习模型的基础，现在最复杂的深度神经网络，拆分到最底层，也可以看到线性模式发挥了巨大的作用。

3. 线性回归（linear regression）模型

0x1：线性回归的发展起源

“回归”是由英国著名生物学家兼统计学家高尔顿(Francis Galton,1822～1911，生物学家达尔文的表弟)在研究人类遗传问题时提出来的。

为了研究父代与子代身高的关系，高尔顿搜集了1078对父亲及其儿子的身高数据。他发现这些数据的散点图大致呈直线状态，也就是说，总的趋势是父亲的身高增加时，儿子的身高也倾向于增加。但是，高尔顿对试验数据进行了深入的分析，发现了一个很有趣的现象，回归效应。

当父亲高于平均身高时，他们的儿子身高比他更高的概率要小于比他更矮的概率；
父亲矮于平均身高时，他们的儿子身高比他更矮的概率要小于比他更高的概率

它反映了一个规律，即这两种身高父亲的儿子的身高，有向他们父辈的平均身高回归的趋势。这就是统计学上最初出现“回归”时的涵义，高尔顿把这一现象叫做“向平均数方向的回归” (regression toward mediocrity)。

对于这个一般结论的解释是：大自然具有一种约束力，使人类身高的分布相对稳定而不产生两极分化，这就是所谓的回归效应。

0x2：线性回归定义

线性回归分析（Linear Regression Analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。本质上说，这种变量间依赖关系就是一种线性相关性，线性相关性是线性回归模型的理论基础。

例如：

一个地区的房价：由面积、地段、层数、周边配套等因素线性组成
孩子的身高：由父亲和母亲的身高两个因素线性组成

线性回归要做的是就是找到一个数学公式能相对较完美地把所有自变量组合（加减乘除）起来，得到的结果和目标接近。这里的所谓“数学公式”就是一个线性模型：

y = w₀ + w₁a₁ + .... + w_ka_k

这里y是连续的属性值，w₀，w₁，...，w_k是权值。

在统计学中，线性回归（Linear regression）是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间的关系（关系就是要通过训练样本获得的知识）进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。

笔者提醒：

读者朋友可能知道，在机器学习中存在很多损失函数，但是线性回归模型一般只能使用最小二乘（MSE）损失函数。这是因为回归分析中，MSE的误差满足正态假设。换句话说，在线性回归中，使用MSE等价于获得极大似然估计。

但是要注意的是，在0/1分类线性分类中，正态误差假设不成立了，因此不能继续使用MSE进行误差估计，需要改用例如交叉熵这种概率评估方法。这点我们后面还会讨论到。

0x3：从一元线性回归说起

在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析（就是我们最熟悉的y=f(x)函数）。

1. 一个广告公司销售额回归预测问题

比方说有一个公司，每月的广告费用和销售额，如下表所示

如果我们把广告费和销售额画在二维坐标内，就能够得到一个散点图，如果想探索广告费和销售额的关系，就可以利用一元线性回归做出一条拟合直线

2. 这条线是怎么画出来的？

很自然地，我们要思考一个问题：我们能不能画出这样一条直线，它能很好地解释历史上广告费和销售额的关系，并且还能帮助我们预测将来新的投入更多的广告费，销售额能到的具体数值。

我们假设这样一个一元线性方程：

Y = ax + b（a、b分别代表2个参数，是我们需要通过观察数据计算得到的）

但是我们发现，这里的a、b参数可能的取值空间是无限的，就算是如上图所示的基本和点集拟合的直线，上下稍微微调一些也是无限的，那到底选哪一条是"相对最精确"的呢？

要知道，绝对精确是不可能的，误差总是存在的。很自然地，我们需要引入一个"标准"来评价模型参数空间中，哪一个是最好的，这就是经验损失函数。接下来的问题是，选什么样的函数呢？

3. 线性回归的损失函数必须选择最小二乘损失！高斯如是说

数学家高斯，通过推导理论证明了，线性回归模型的损失函数必须是最小二乘损失。

线性回归方程预测的结果是存在随机误差的，比如某一组特征值，真实值和预测值之间存在误差。按照高斯随机误差定理（由大量随机误差组成的事件总误差满足高斯分布），假设误差满足高斯分布，那么误差的概率密度函数为：

将均方损失函数公式代入上式，得到下式：

我们发现以上就是拟合数据集的最大似然函数，通过求似然函数的极大值来获取最优参数θ，对似然函数两边取log并不影响获取极大值的的参数θ，即：

为简便记忆上面的结论，可做以下推导：

高斯通过推导证明了：在一个符合高斯随机误差假设的线性模式中，基于最小二乘损失函数求解模型参数的过程，本质上就是在求解模型参数的极大似然估计。

4. 回到我们广告预测的例子

有了上面额讨论，对于广告费和销售额的那个例子，我们就可以算出那条拟合直线具体是什么，分别求出公式中的各种平均数，然后带入即可，最后算出a=1.98，b=2.25

最终的回归拟合直线为：

Y=1.98X+2.25

利用该线性回归模型可以对未来做一些预测，比如如果投入广告费2万，那么预计销售额为6.2万。

5. 为什么对历史数据拟合的看起来不是那么准？

上面得到了回归拟合直线：Y=1.98X+2.25，但是我们仔细观察一下会发现这条回归直线对历史数据拟合的并不是那么准，很多的点都没有落在直线上。这是为什么呢？

对这个问题，存在几个原因：

数据集本身存在异常噪音点（noise data）：样本本身可能存在一些“离群异常点”，这些点本身不存在任何线性相关关系。
数据集中包含非线性数据（non linear problem）：这可能是个严重的问题，意味着我们的建模就错误了，目标问题根本就不是一个线性关系问题，强行用线性模型拟合肯定是不行的。
异质性（欠特征化）：导致因变量的自变量不在我们选取的特征中，换句话说，即我们选择的特征不能很好的体现出线性型的特征。对于销售额这个例子来说，其实广告费只是影响销售额的其中一个比较重要的因素，可能还有经济水平、产品质量、客户服务水平等众多难以说清的因素在影响最终的销售额，那么实际的销售额就是众多因素相互作用最终的结果，由于销售额是波动的，回归线只表示广告费一个变量的变化对于总销售额的影响，所以必然会造成偏差，回归线只能解释了一部分影响。

这就反回来启发我们，应该用一个更加切近真实情况的损失评估标准来评估我们的回归线，为了引入这个新的损失评估标准，我们先来引入二个新的评价指标。

6. 两个新的评价指标

SST（总偏差）= SSR（回归线可以解释的偏差）+ SSE（回归线不能解释的偏差）

总偏差平方和（SST，Sum of Squaresfor Total）：是每个因变量的实际值（给定点的所有Y）与因变量平均值（给定点的所有Y的平均）的差的平方和，即，反映了因变量取值的总体波动情况。实际上也就是方差。
回归平方和（SSR，Sum of Squares forRegression）：因变量的回归值（直线上的Y值）与其均值（给定点的Y值平均）的差的平方和，即，它是由于自变量x的变化引起的y的变化，反映了y的总偏差中由于x与y之间的线性关系引起的y的变化部分，是可以由回归直线来解释的
残差平方和（又称误差平方和，SSE，Sum of Squaresfor Error）：因变量的各实际观测值(给定点的Y值)与回归值（回归直线上的Y值）的差的平方和，它是除了x对y的线性影响之外的其他因素对y变化的作用，是不能由回归直线来解释的

R²= SSR/SST 或 R²= 1-SSE/SST

R²的取值在0，1之间，越接近1说明拟合程度越好。

可以看到，我们将SSR（回归线可以解释的偏差）除以(归一化)一个总偏差，以此来更加准确地评估我们的回归线对真实情况的拟合。

假如所有的点都在回归线上，说明SSE为0，则R²=1，意味着Y的变化100%由X的变化引起，没有其他因素会影响Y，回归线能够完全解释Y的变化
如果R2很低，说明Y的变化不完全由X的波动决定，X和Y之间可能不存在线性关系

实际上，这两个指标在概率论与数理统计里中有类似的概念，叫做相关系数R（学名是皮尔逊相关系数，因为这不是唯一的一个相关系数，而是最常见最常用的一个），R用来表示X和Y作为两个随机变量的线性相关程度，取值范围为【-1，1】。

R=1：说明X和Y完全正相关，即可以用一条直线，把所有样本点（x,y）都串起来，且斜率为正
R=-1：说明完全负相关，及可以用一条斜率为负的直线把所有点串起来
R=0：则说明X和Y没有线性关系，注意，是没有线性关系，说不定有其他关系(例如非线性关系)

还是回到最开始的广告费和销售额的例子，这个回归线的R^2为0.73，说明广告费和营业额之间存在相对较高的相关性，且拟合程度还可以。

Relevant Link:

http://scikit-learn.org/stable/auto_examples/linear_model/plot_ols.html#sphx-glr-auto-examples-linear-model-plot-ols-py
http://www.jianshu.com/p/fcd220697182
http://studyai.site/2016/07/22/%E6%96%AF%E5%9D%A6%E7%A6%8F%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E8%AF%BE%E7%A8%8B%20%E7%AC%AC%E4%B8%80%E5%91%A8%20(4)%E4%B8%80%E5%85%83%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92/
https://baike.baidu.com/item/%E4%B8%80%E5%85%83%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92%E9%A2%84%E6%B5%8B%E6%B3%95

0x4：扩展到多元线性回归

将上面一元的例子推广到多元的情况。多元线性回归模型（multivariable linear regression model ）

在实际经济问题中，一个变量往往受到多个变量的影响，有时几个影响因素主次难以区分，或者有的因素虽属次要，但也不能略去其作用。例如，家庭消费支出，除了受家庭可支配收入的影响外，还受诸如家庭所有的财富、物价水平、金融机构存款利息等多种因素的影响。在这种复杂问题的拟合中，我们要用到多元线性函数。

所谓多元回归分析预测法，是指通过对两个或两个以上的自变量与一个因变量的相关分析，建立预测模型进行预测的方法。当自变量与因变量之间存在线性关系时，称为多元线性回归分析

1. 多元线性模型数学公式

假定被解释变量与多个解释变量之间具有下面的线性关系（即满足下面关于变量X的多元线性函数），则称X和Y的关系组成了一个多元线性回归模型

其中：

为被解释变量
为个解释变量
为个未知参数
为随机误差项

可以看到，多元线性函数其实是由很多个一元线性函数线性组合而成

对于组观测值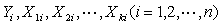，其方程组形式为：

即

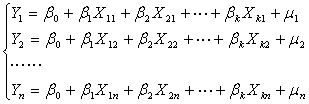
其矩阵形式为

即：，其中

为被解释变量的观测值向量
为解释变量的观测值矩阵
为总体回归参数向量
为随机误差项向量。

总体回归方程表示为：

2. 根据训练样本(观测数据)来推测出多元线性模式的参数 - 最大似然估计思想

多元线性回归模型包含多个解释变量，多个解释变量同时对被解释变量发生作用，若要考察其中一个解释变量对的影响就必须假设其它解释变量保持不变来进行分析。

因此多元线性回归模型中的回归系数为偏回归系数，即反映了当模型中的其它变量不变时，其中一个解释变量对因变量的均值的影响。

由于参数都是未知的，可以利用样本观测值对它们进行估计。若计算得到的参数估计值为，用参数估计值替代总体回归函数的未知参数，则得多元线性样本回归方程：

其中：

为参数估计值
为的样本回归值或样本拟合值、样本估计值

其矩阵表达形式为:

其中：

为拟合值列向量
为阶样本观测矩阵
为阶参数估计值列向量

3. 多元线性模型下怎么评估拟合程度的好坏？

1）残差平方估计

和一元线性回归一样，在多元的情况下也可以使用最小二乘估计来得到拟合值和实际值的差距

观测值与回归值的残差为：

由最小二乘法可知从训练样本估计得到的参数估计值应使全部观测值与回归值的残差的平方和最小，即使

取得最小值。根据多元函数的极值原理，分别对求一阶偏导，并令其等于零，即

展开有：

化简得下列方程组：

上述个方程称为正规方程，其矩阵形式为：

因为

且

设为参数估计值向量，根据上式可得到正规方程组：

2）可决系数 $R 2$

与一元线性回归中可决系数 $r 2 相对应，多元线性回归中也有多重可决系数 r 2 ，它是在因变量的总变化中，由回归方程解释的变动(回归平方和)所占的比重， R 2 越大，回归方各对样本数据点拟合的程度越强，所有自变量与因变量的关系越密切。计算公式为：$

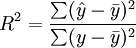
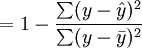
$R^2=\frac{\sum(\hat{y}-\bar{y})^2}{\sum(y-\bar{y})^2}$ $=1-\frac{\sum(y-\hat{y})^2}{\sum(y-\bar{y})^2}$

分母表示实际值和实际均值的残差平方和，分子表示拟合值和实际均值的残差平方和

3）估计标准误差

估计标准误差，即因变量y的实际值与回归方程求出的估计值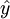 $\hat{y}$ 之间的标准误差，估计标准误差越小，回归方程拟合程度越好

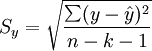
$S_y=\sqrt{\frac{\sum(y-\hat{y})^2}{n-k-1}}$

其中，k为多元线性回归方程中的自变量的个数。除此之后还显著性检验，F检验等，本质上都类似的，都是用来评估拟合值和真实值之间的差距程度，这里就不一一列举。

笔者提醒：注意多重共线性问题
多重共线性是指在多元线性回归方程中，自变量之间有较强的线性关系，这种关系若超过了因变量与自变量的线性关系，则回归模型的稳定性受到破坏，回归系数估计不准确。

需要指出的是，在多元回归模型中，多重共线性的难以避免的，只要多重共线性不太严重就行了。判别多元线性回归方程是否存在严惩的多重共线性，可分别计算每两个自变量之间的可决系数r2，若r2 > R2或接近于R2，则应设法降低多重线性的影响降低多重共线性的办法主要是转换自变量的取值，如“变绝对数为相对数或平均数”，或者”更换其他的自变量“。

Relevant Link:

http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html 
https://zh.wikipedia.org/wiki/%E7%B7%9A%E6%80%A7%E5%9B%9E%E6%AD%B8
https://medium.com/towards-data-science/simple-and-multiple-linear-regression-in-python-c928425168f9https://baike.baidu.com/item/%E5%A4%9A%E5%85%83%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92%E6%A8%A1%E5%9E%8B
http://www.cnblogs.com/dfcao/p/ng_ml_2.html
http://www.cnblogs.com/zgw21cn/archive/2008/12/24/1361287.html 
https://onlinecourses.science.psu.edu/stat501/node/311
http://wiki.mbalib.com/wiki/%E5%A4%9A%E5%85%83%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92%E9%A2%84%E6%B5%8B

4. 线性分类（linear classification）模型

0x1：从多响应线性回归（multiresponse linear regression）说起

线性回归法可以方便地应用于数值预测任务中。事实上，任何回归技术，无论是线性的还是非线性的，都可以用来做分类任务。技巧是对每一个类执行一个回归，使属于该类的训练实例的输出结果为1，而不属于该类的输出结果为0，最终得到该类的一个线性表达式。然后，对一个给定的未知类的测试实例，计算每个线性表达式的值并选择其中最大的，这种方法有时称为多响应线性回归。

叶子节点为线性回归模型的决策树，线性模式得到的数值需要再转化为一个概率值

如上图所示，一种查看多响应线性回归的方法是将线性表达式想象成与每个类对应的数值型的隶属函数（membership function）。

对于属于这个类的实例，隶属函数值为1
对于其他类的实例，函数值为0

对于一个新给出的实例，计算新实例与各个类的从属关系，从中选择从属关系最大的一个。

在实际应用中，多响应线性回归通常能产生很好的结果，但是也存在两个缺点：

第一、隶属函数产生的不是概率值，从属关系值可能落在0~1之外
第二、最小二乘回归假设误差之间彼此独立，所有误差综合起来得到一个标准正态分布，当多响应线性回归用于分类问题时，明显违背了这个假设，因为这时观察值仅呈现0和1，是一种阶跃分布

解决这个问题的学术演进是 Logistic回归（Logistic regression）的统计技术，我们接下来展开讨论。

0x2: 逻辑斯蒂回归（Logistic regression）分类模型

逻辑斯蒂回归（logistic regression）是统计学中的经典分类方法，它属于对数线性模型。逻辑斯蒂回归模型源自逻辑斯蒂分布，其分布函数F(x)是S形函数。逻辑斯蒂回归模型是由输入的线性函数表示的输出的对数几率模型。

这么说有些抽象，我们来看看logistic regression是如何改进linear regression的。

1. 逻辑斯蒂分布（logistic distribution）模型对线性回归（linear regression）的改机

首先假设只有两个类的情况，logistic regression将原始目标变量：

这个无法用线性函数来正确地近似表达的变量，替换为：

结果值将不再局限于0~1，而是无穷大和无穷小之间的任意值，如下图：

这种变换我们称之为对数变换（logit transformation）。

转换后的变量使用一个线性函数来近似，就像是由线性回归法所建立的函数，结果模型是：

这里权值为w，下图展示了该函数在1维数据空间上的一个例子，w₀=-0.125，w₁=0.5。

2. Logistic regression模型概率公式

逻辑斯谛分布是指连续随机变量X具备下列分布函数和密度函数

其中，u为未知参数，r > 0为形状参数，如下图：

可以看到，逻辑斯谛分布函数是一条S形曲线（sigmoid curve），该曲线以点（u, 1/2）为中心对称。曲线在中心附近增长速度较快，在两端增长速度较慢：

形状参数r的值越小，曲线在中心附近增长得越快，也即越接近阶跃函数
阶跃点由位置参数u决定

3. 由逻辑斯蒂回归模型得到的对数几率线性模式

我们前面说过，逻辑斯蒂回归模型属于对数线性模型，通过两边加入对数log，可以让逻辑斯蒂回归呈现出线性形式，这种线性形式我们称之为”几率（odds）“。

一个事件的几率（odds）指该事件发生与不发生的概率比值，若事件发生概率为

上式中可以看出，输出Y=1的对数几率是由输入x的线性函数表示的模型。当 w⋅x的值越接近正无穷，P(Y=1|x) 概率值也就越接近1。

进一步的，上式就是神经网络中sigmoid激活函数的形式，每一个sigmoid函数就是一个决策单元。

4. 逻辑斯蒂回归模型参数估计

logistic regression模型建立后，接下来如何去求解模型中的参数。在统计学中，常常使用极大似然估计法来求解，即找到一组参数，使得在这组参数下，我们的训练样本数据被正确分类的似然度（概率）最大。

损失函数可以有很多选择，但是不能继续用最小二乘损失函数进行最大似然估计，的原因前面说过了，因为误差假设条件不成立了。常用的损失函数是交叉熵代价函数，它的理论基础是KL散度最小化原则。

逻辑斯蒂回归模型学习时，对于给定的训练数据集T = {（x1, y1），（x2，y2），....，（xn, yn）}，设：

似然函数（likelihood）如下：

对数对数似然函数（log-likelihood）如下：

现在要求

实际上，对数似然损失在单个数据点上的定义为：

如果取整个数据集上的平均对数似然损失，我们恰好可以得到:

由此可以看到，在逻辑回归模型中，最大化似然函数和最小化对数似然损失函数这两种策略实际上是等价的。损失函数背后的本质还是似然概率分布原理。

5. 多项式逻辑斯蒂回归（多项代表label有多种可能）

在大于2的多分类问题中，要用到多项式逻辑斯蒂回归模型（multi-nominal logistic regression model）。假设离散型随机变量Y的取值集合是｛1，2，...，K｝，则模型公式为：

同样，二项逻辑斯蒂回归的参数估计法也可以推广到多项逻辑斯蒂回归。

逻辑斯蒂回归比线性回归优势在于：线性回归在整个实数域内敏感度一致。而逻辑回归就是一种减小预测范围，将预测值限定为[0,1]间的一种回归模型。逻辑曲线在z=0时，十分敏感，这让模型能够对数据集中细节的差别具备较灵敏的分类能力（未知参数r越小，灵敏度越高），在z>>0或z<<0处（两头位置），都不敏感。

逻辑斯蒂回归可以看成是一个通过log压缩到【0，1】值域中的线性回归模型

Relevant Link:

http://blog.csdn.net/xbinworld/article/details/43919445
http://blog.sciencenet.cn/blog-427701-688352.html
http://blog.csdn.net/ppn029012/article/details/8775597
http://blog.csdn.net/richard2357/article/details/17241039
http://blog.sciencenet.cn/blog-508318-633085.html
http://blog.csdn.net/daunxx/article/details/51816588
https://chenrudan.github.io/blog/2016/01/09/logisticregression.html
http://www.52cs.org/?p=286
https://www.zhihu.com/question/21329754/answer/18004852
https://yoyoyohamapi.gitbooks.io/mit-ml/content/%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92/articles/%E5%9B%9E%E5%BD%92%E9%97%AE%E9%A2%98.html

0x3：感知机，一种简单的逻辑回归模型

logistic回归试图通过将训练数据的概率最大化的方法，产生正确的概率估计。现在假设只有两个类，如果使用一个超平面能够将数据完美地分成两组，那么就称该数据为线性可分（linearly separable）数据。

如果数据是线性可分的，那么就有一个非常简单的算法用于寻找一个分隔超平面，这种算法称为感知机学习规则（perceptron learning rule）。

感知机使用“y是否大于0”作为判别法则，把结果 y > 0和y < 0对应的输入 x 分成两类。我个人更愿意将其理解为简化版本的逻辑斯蒂回归，因为从图上就可以看到，感知机对区别度较大的样本分类效果很好，但是对区别度较小的（靠近0）的中间那块，这样一刀切的方式就很容易造成误报和漏报

但其本质还是：基于线性回归的结果，进行离散化得到有限个分类结果。和上面讨论的典型线性分类算法核心思想是一样的

0x4: 最大熵模型，逻辑斯蒂回归的一般泛化形式

在了解了logistic regression的基本定义后，我们来对概念进一步地抽象泛化，讨论一个更一般的理论框架。我们先从最大熵原理说起。

1. 最大熵原理

最大熵模型（maximum entropy model）由最大熵原理推导实现。最大熵原理是概率模型学习中的一个准则，即：

学习概率模型时，在所有可能的概率模型（分布）中，熵最大的模型是最好的模型。最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型。

假设离散随即变量X的概率分布是P(X)，则其熵为：

根据信息论原理，熵满足下列不等式：

，其中| X |代表X的取值个数，当且仅当X的分布是均匀分布时右边的等号成立，即当X服从均匀分布时，熵最大。

直观地说，最大熵原理认为要选择的概率模型首先必须满足目前已有的事实，即约束条件。在没有更多信息的情况下，那些不确定的部分都是"等可能的"（即等概率）。

最大熵原理通过熵的最大化来表示等可能性。"等可能性"不好公式化，而熵则是一个可优化逼近的数值指标。

2. 最大熵模型的定义

最大熵原理是统计学的一般原理，将它应用到分类得到最大熵模型。在进行下面推导之前，我们需要先定义一些数学符号：

π(x)_u：输入时

我们的目标，就是从训练数据中，学习得到一个模型，使得

基于信息论理论，我们可以得到

根据最大熵原理，需要让该熵公式，也就是目标（策略）

在k=2的情况下，最大熵模型退化为逻辑斯蒂回归模型。

3. 最大熵模型和逻辑斯蒂模型联系与区别总结

逻辑回归跟最大熵模型没有本质区别。逻辑回归是最大熵对应类别为二类时的特殊情况
概率函数指数簇分布的最大熵等价于其指数形式的最大似然函数
二项式分布的最大熵解等价于二项式指数形式(sigmoid)的最大似然函数
多项式分布的最大熵等价于多项式分布指数形式(softmax)的最大似然函数

Relevant Link:

http://blog.csdn.net/cyh_24/article/details/50359055

5. 从函数优化这个统一视角看线性回归和线性分类模型的区别与联系

0x1：从输入输出角度看"回归"和"分类"的区别

线性分类问题和线性回归问题都要根据训练样本训练出一个实值函数g(x)，g(x)也叫映射函数

回归模型: 给定一个新的输入特征，推断它所对应的输出y(连续值实值)是多少, 也就是使用y=g(x)来推断任一输入x所对应的输出值。
分类模型: 给定一个新的输入特征, 推断它所对应的类别(大多数情况是二分类如: +1, -1，也可以基于二分类扩展出多分类), 也就是使用y=sign(g(x))来推断任一输入x所对应的类别。注意，模型的输出结果类别是有限的

0x2：从损失评估标准角度看"回归"和"分类"的区别

线性回归模型的损失评估是：(输出值) compare (输入值)
线性分类模型的损失评估是：(输出值) compare (F(输入值))，这里F(输入值)指依照某个标准将输入值映射为某些特定的类值

0x3：从决策超平面空间分布角度看"回归"和"分类"的区别

从线性方程组角度看，线性回归和线性分类的底层都是一组（w₁，....，w_n）权值向量参数。

而输入输出结果的不同，以及损失评估标准的不同，进一步导致了线性回归方程组和线性分类方程组的权值向量不同。

线性回归方程组的权重向量超平面是一个”靠近“数据集的超平面
线性分类方程组的权重向量超平面是一个”原理“数据集中不同类别的超平面决策面

0x4：回归和分类各自的应用场景

回归问题的应用场景 - 回归是对真实值的一种"逼近预测"
- 回归问题通常是用来预测一个值，如预测房价、未来的天气情况等等
- 例如一个产品的实际价格为500元，通过回归分析预测值为499元，我们认为这是一个比较好的回归分析
- 预测明天的气温是多少度，这是一个回归任务
分类问题的应用场景 - 分类并没有逼近的概念，最终正确结果只有一个，错误的就是错误的，不会有相近的概念
- 分类问题是用于将事物打上一个标签，通常结果为离散值
- 例如判断一幅图片上的动物是一只猫还是一只狗)
- 预测明天是阴、晴还是雨，就是一个分类任务，但是很容易理解

总体来说，回归模型对精度要求更低，它允许模型包含一定的误差，只要不影整体拟合结果即可

Relevant Link:

http://blog.csdn.net/caroline_wendy/article/details/13294893
https://my.oschina.net/zzw922cn/blog/544221?p=1
http://www.jianshu.com/p/d6f206c869ed
http://zh.numberempire.com/derivativecalculator.php
https://www.zhihu.com/question/21329754
https://hellozhaozheng.github.io/z_post/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0-%E9%80%BB%E8%BE%91%E5%9B%9E%E5%BD%92/

6. 从鸢尾花例子看回归和分类问题的共性和区别

笔者写这章的面对是希望向读者朋友传递一个观点：logistic regression只是一种利用linear regression的形式，并不代表线性分类只有logistic regression这一种形式。

线性分类的真正底层思想是：线性回归模型的归一化，这个归一化可以是概率0~1化，也可以是离散化。

我们用我们最熟悉的鸢尾花数据集作为例子，来说明这个概念。

0x1: 前2维特征+4维PCA降维到3维的可视化数据集展示

鸢尾花数据集是一个很经典的数据集，每个样本包含4个维度的特征：的花瓣和萼片长度和宽度。样本量150个，label标签有Setosa,Versicolour、Virginica这3种

# -*- coding: utf-8 -*-

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import datasets
from sklearn.decomposition import PCA

if __name__ == '__main__':
    # import some data to play with
    iris = datasets.load_iris()
    X = iris.data[:, :2]  # we only take the first two features.
    y = iris.target

    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5

    plt.figure(2, figsize=(8, 6))
    plt.clf()

    # Plot the training points
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1,
                edgecolor='k')
    plt.xlabel('Sepal length')
    plt.ylabel('Sepal width')

    plt.xlim(x_min, x_max)
    plt.ylim(y_min, y_max)
    plt.xticks(())
    plt.yticks(())

    # To getter a better understanding of interaction of the dimensions
    # plot the first three PCA dimensions
    fig = plt.figure(1, figsize=(8, 6))
    ax = Axes3D(fig, elev=-150, azim=110)
    X_reduced = PCA(n_components=3).fit_transform(iris.data)
    ax.scatter(X_reduced[:, 0], X_reduced[:, 1], X_reduced[:, 2], c=y,
               cmap=plt.cm.Set1, edgecolor='k', s=40)
    ax.set_title("First three PCA directions")
    ax.set_xlabel("1st eigenvector")
    ax.w_xaxis.set_ticklabels([])
    ax.set_ylabel("2nd eigenvector")
    ax.w_yaxis.set_ticklabels([])
    ax.set_zlabel("3rd eigenvector")
    ax.w_zaxis.set_ticklabels([])

    plt.show()

明确了数据集长什么样，我么接下来开始进行一个小实验，说逐步说明我们什么时候该用线性回归/非线性回归，什么时候该用分类模型，以及回归与分类的关系。

在开始之前，我需要明确一下我们的目标：建立一个模型(任意模型)，当我输入鸢尾花的特征之后，模型需要告诉我这个鸢尾花属于哪一类？

0x2: 先用一元线性回归模型试试？

也许直觉上这个问题不适合用一元线性回归模型来做，但是我这里执意要这么做，并且要最大程度地发挥一元线性回归模型的威力使其帮助我们尽可能地好的去靠近这个目标

1. 选择和待预测值Y相关性最强的一个特征

我们只能选择一个特征，那肯定要选择一个能达到最好拟合预测能力的特征，使用可决系数R2的来帮我们评估

Feature_1 - Variance score: 0.58
Feature_2 - Variance score: 0.26
Feature_3 - Variance score: 0.90
Feature_4 - Variance score: 0.92

从可决系数的比较上来看，第4个特征和待拟合值的相关性最好，我们选择特征4。

2. 建立一元线性回归模型

用X轴表示特征4，用Y轴表示label，通过plot可视化出来

# -*- coding: utf-8 -*-

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score

if __name__ == '__main__':
    # import some data to play with
    iris = datasets.load_iris()

    # Use only one feature
    diabetes_X = iris.data[:, 3:4]  # we only take the two features.
    diabetes_y = iris.target

    # Split the data into training/testing sets
    split_len = int(len(diabetes_X) * 0.8)
    diabetes_X_train = diabetes_X[:split_len]
    diabetes_X_test = diabetes_X[split_len:]
    print "diabetes_X_train"
    print diabetes_X_train

    # Split the targets into training/testing sets
    diabetes_y_train = diabetes_y[:split_len]
    diabetes_y_test = diabetes_y[split_len:]
    print "diabetes_y_train"
    print diabetes_y_train

    # Create linear regression object
    regr = linear_model.LinearRegression()

    # Train the model using the training sets
    regr.fit(diabetes_X_train, diabetes_y_train)

    # Make predictions using the testing set
    diabetes_y_pred = regr.predict(diabetes_X_train)
    print "diabetes_y_pred"
    print diabetes_y_pred

    # 对线性回归模型的预测值进行离散采样归一化
    '''
    diabetes_y_pred_normal = list()
    for pred in diabetes_y_pred:
        if pred <= 0.5:
            diabetes_y_pred_normal.append(0.)
        elif pred <= 1.5:
            diabetes_y_pred_normal.append(1.)
        else:
            diabetes_y_pred_normal.append(2.)
    diabetes_y_pred = np.array(diabetes_y_pred_normal)
    print "diabetes_y_pred"
    print diabetes_y_pred
    '''

    # The coefficients
    print('Coefficients: ', regr.coef_)
    # The mean squared error
    # Explained variance score: 1 is perfect prediction
    # 可决系数R2越接近1，说明特征和拟合值的相关性越大
    print('Variance score: %.2f' % r2_score(diabetes_y_train, diabetes_y_pred))
    # 预测的准确度
    print "Prediction accurate: %2f" % np.mean(diabetes_y_pred == diabetes_y_train)

    # Plot outputs
    plt.scatter(diabetes_X_train, diabetes_y_train, color='black')
    plt.scatter(diabetes_X_train, diabetes_y_pred, color='blue', linewidth=3)

    plt.xticks(())
    plt.yticks(())

    plt.show()

黑色的点代表样本实际值，蓝色的点代表一元线性模型拟合值。

3. 我们要预测的是[0, 1, 2]这3种离散的label类型，你给我一个连续性的线性回归模型怎么用？

得到的这个模型我们会发现无法进行预测，因为线性回归模型得到的值是连续值

我们先不要想当然地就回答说用逻辑回归来做线性分类，我们来一起思考下。

为了解决这个问题，我们前面说过，我们可以对线性回归模型的连续预测值进行离散化采样，采样点的分界面(对一维来说就是分界线)可以大致假定一个0.5和1.5，即取【0，1，2】的中位数，进行了离散采样归一化之后的结果如下

图中的两个箭头就是分界线

注意x(Y = 1.5)(Y值为1.5的x点)那个分界线，在分界线的两边都存在误分类(即误报)。

对这种情况。我们也许可以建立一个损失函数的策略，即根据均方误差损失函数去求得最佳分类线X。

这个例子很简单，从直观上就可以看出，第二个分界线不管怎么左右调整，损失函数都不可能降到0，因为在它的分类维度上，点集Y=1和点集Y=2是存在重合的，换句话说，点集Y=1和点集Y=2在当前特征维度上是线性不可分的，那么就不可能用线性函数进行完美分类，数据本身和维度的限制限制了最终的效果。

0x3: 多元线性回归模型入场？

既然一元回归模型维度太少了，我们就把维度提高，根据SVM核函数的思想，在低纬度不可分的数据集在高维度就有更大的可能是线性可分的，1维的分界线到了高维度变成了超分类面。

为了便于理解，我们来看一个4维PCA后的3维点集图：

可以看到，应该相对容易地我们用2个垂直于"2nd eigenvector" x "1st eigenvector"平面作为分类面，可以较好地把3类数据集给切分开来。

基于这个观察，我们改变策略：

这次同时用上鸢尾花的全部4个特征(当然其实这里是否要同时用到4个特征，也是值得展开的一个话题，严格地说这里应该进行特征选择工程，但我们暂时忽略)
离散采样标准还是x(Y = 0.5)、x(Y = 1.5)，取样本Y实际值的中位数对应的X点作为超分界面，只是这时候X不在是一个线，而是一个4维超平面

训练集得到的模型对训练集本身的离散化预测结果如下

Variance score: 0.98
Prediction accurate: 0.991667

这次的整体可决系数和准确度都得到的大幅度提高，对测试集的泛化能力也不错，达到了80%

0x4: 使用非线性回归模型试试？

我们试着用非线性回归模型来帮助我们更好地拟合样本点，得到的实验结果在多元线性回归模型上有进一步提升。

0x5: 使用Logistic regression对数据集进行分类

逻辑斯蒂回归模型是在回归模型的基础上进行概率归一化采样得到分类结果，本质上也是一种非线性回归模型。

#!/usr/bin/python
# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model, datasets

# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2]  # we only take the first two features.
Y = iris.target

h = .02  # step size in the mesh

logreg = linear_model.LogisticRegression(C=1e5)

# we create an instance of Neighbours Classifier and fit the data.
logreg.fit(X, Y)

# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = logreg.predict(np.c_[xx.ravel(), yy.ravel()])

# 预测的准确度
X_pre = logreg.predict(X)
print X_pre
print "Prediction accurate: %2f" % np.mean(X_pre == Y)


# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(4, 3))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)

# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=Y, edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')

plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())

plt.show()

每次判断时，多项式逻辑斯蒂回归模型基于最大似然估计原理，根据样本在所有条件概率中最大的对应的那个类作为最终判断结果（softmax）

可以看到，用逻辑斯蒂回归模型对鸢尾花的2个特征进行分类，得到了80%的准确度

0x6: 使用SVM直接寻找超分类面对数据集进行分类

SVM不进行回归训练，而是直接寻找最优超分类面

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets


def make_meshgrid(x, y, h=.02):
    """Create a mesh of points to plot in

    Parameters
    ----------
    x: data to base x-axis meshgrid on
    y: data to base y-axis meshgrid on
    h: stepsize for meshgrid, optional

    Returns
    -------
    xx, yy : ndarray
    """
    x_min, x_max = x.min() - 1, x.max() + 1
    y_min, y_max = y.min() - 1, y.max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))
    return xx, yy


def plot_contours(ax, clf, xx, yy, **params):
    """Plot the decision boundaries for a classifier.

    Parameters
    ----------
    ax: matplotlib axes object
    clf: a classifier
    xx: meshgrid ndarray
    yy: meshgrid ndarray
    params: dictionary of params to pass to contourf, optional
    """
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    out = ax.contourf(xx, yy, Z, **params)
    return out


# import some data to play with
iris = datasets.load_iris()
# Take the first two features. We could avoid this by using a two-dim dataset
X = iris.data[:, :2]
y = iris.target

# we create an instance of SVM and fit out data. We do not scale our
# data since we want to plot the support vectors
C = 1.0  # SVM regularization parameter
models = (svm.SVC(kernel='linear', C=C),
          svm.LinearSVC(C=C),
          svm.SVC(kernel='rbf', gamma=0.7, C=C),
          svm.SVC(kernel='poly', degree=3, C=C))
models = (clf.fit(X, y) for clf in models)

# title for the plots
titles = ('SVC with linear kernel',
          'LinearSVC (linear kernel)',
          'SVC with RBF kernel',
          'SVC with polynomial (degree 3) kernel')

# Set-up 2x2 grid for plotting.
fig, sub = plt.subplots(2, 2)
plt.subplots_adjust(wspace=0.4, hspace=0.4)

X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)

for clf, title, ax in zip(models, titles, sub.flatten()):
    plot_contours(ax, clf, xx, yy,
                  cmap=plt.cm.coolwarm, alpha=0.8)
    ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
    ax.set_xlim(xx.min(), xx.max())
    ax.set_ylim(yy.min(), yy.max())
    ax.set_xlabel('Sepal length')
    ax.set_ylabel('Sepal width')
    ax.set_xticks(())
    ax.set_yticks(())
    ax.set_title(title)

plt.show()

Relevant Link:

https://en.wikipedia.org/wiki/Iris_flower_data_set
http://scikit-learn.org/stable/auto_examples/datasets/plot_iris_dataset.html
http://scikit-learn.org/stable/auto_examples/index.html
http://blog.csdn.net/golden1314521/article/details/46564227
http://scikit-learn.org/stable/auto_examples/semi_supervised/plot_label_propagation_versus_svm_iris.html#sphx-glr-auto-examples-semi-supervised-plot-label-propagation-versus-svm-iris-py
http://scikit-learn.org/stable/auto_examples/svm/plot_iris.html

posted @ 2017-08-28 22:27 郑瀚阅读(2797) 评论(0) 编辑收藏举报

刷新页面返回顶部

Han Zheng, Thinker and Doer

Welcome to contact me. Wechat：LittleHann

从损失函数优化角度：讨论“线性回归（linear regression）”与”线性分类（linear classification）“的联系与区别

1. 主要观点

2. 线性模型，线性回归和线性分类的基础

0x1：线性模型中的“线性”指的是什么

3. 线性回归（linear regression）模型

0x1：线性回归的发展起源

0x2：线性回归定义

0x3：从一元线性回归说起

1. 一个广告公司销售额回归预测问题

2. 这条线是怎么画出来的？

3. 线性回归的损失函数必须选择最小二乘损失！高斯如是说

4. 回到我们广告预测的例子

5. 为什么对历史数据拟合的看起来不是那么准？

6. 两个新的评价指标

0x4：扩展到多元线性回归

1. 多元线性模型数学公式

2. 根据训练样本(观测数据)来推测出多元线性模式的参数 - 最大似然估计思想

3. 多元线性模型下怎么评估拟合程度的好坏？

1）残差平方估计

2）可决系数R2

3）估计标准误差

4. 线性分类（linear classification）模型

0x1：从多响应线性回归（multiresponse linear regression）说起

0x2: 逻辑斯蒂回归（Logistic regression）分类模型

1. 逻辑斯蒂分布（logistic distribution）模型对线性回归（linear regression）的改机

2. Logistic regression模型概率公式

3. 由逻辑斯蒂回归模型得到的对数几率线性模式

4. 逻辑斯蒂回归模型参数估计

5. 多项式逻辑斯蒂回归（多项代表label有多种可能）

0x3：感知机，一种简单的逻辑回归模型

0x4: 最大熵模型，逻辑斯蒂回归的一般泛化形式

1. 最大熵原理

2. 最大熵模型的定义

3. 最大熵模型和逻辑斯蒂模型联系与区别总结

5. 从函数优化这个统一视角看线性回归和线性分类模型的区别与联系

0x1：从输入输出角度看"回归"和"分类"的区别

0x2：从损失评估标准角度看"回归"和"分类"的区别

0x3：从决策超平面空间分布角度看"回归"和"分类"的区别

0x4：回归和分类各自的应用场景

6. 从鸢尾花例子看回归和分类问题的共性和区别

0x1: 前2维特征+4维PCA降维到3维的可视化数据集展示

0x2: 先用一元线性回归模型试试？

1. 选择和待预测值Y相关性最强的一个特征

2. 建立一元线性回归模型

3. 我们要预测的是[0, 1, 2]这3种离散的label类型，你给我一个连续性的线性回归模型怎么用？

0x3: 多元线性回归模型入场？

0x4: 使用非线性回归模型试试？

0x5: 使用Logistic regression对数据集进行分类

0x6: 使用SVM直接寻找超分类面对数据集进行分类

公告

2）可决系数 $R 2$