线性模型(linear model)基本定义及参数求解数学本质、损失函数的选择与评估数学原理、及其基于线性模型衍生的其他机器学习模型相关原理讨论
1. 线性模型简介
0x1:线性模型的现实意义
在一个理想的连续世界中,任何非线性的东西都可以被线性的东西来拟合(参考Taylor Expansion公式),所以理论上线性模型可以模拟物理世界中的绝大多数现象。而且因为线性模型本质上是均值预测,而大部分事物的变化都只是围绕着均值而波动,即大数定理。
事物发展的混沌的线性过程中中存在着某种必然的联结。事物的起点,过程,高潮,衰退是一个能被推演的过程。但是其中也包含了大量的偶然性因素,很难被准确的预策,只有一个大概的近似范围。但是从另一方面来说,偶然性自身也可以组成一条符合大数定理的线性。
0x2:线性模型的基本形式
给定有d个属性描述的示例,线性模型试图学得一个通过属性的线性组合来进行预测的函数,即:
一般用向量形式写成:![]() ,其中,
,其中,![]() ;
;
线性模型中 f(x) 可以是各种“尺度”上的函数,例如:
f(x)为离散的值:线性多分类模型
f(x)为实数域上实值函数:线性回归模型
f(x)为对数:对数线性模式
f(x)进行sigmoid非线性变换:对数几率回归
...
实际上 ,f(x)可以施加任何形式的变换,笔者在这篇blog中会围绕几个主流的变换形式展开讨论,需要大家理解的是,不同的变换之间没有本质的区别,也没有好坏优劣之分,不同的变换带来不同的性质,而不同的性质可以用于不同的场景。
1. 线性模型参数求解的本质 - 线性方程组求解
不管对 f(x) 施加什么样的变化,从方程求解角度来看,是一个线性方程组。
在这个方程组中,x 是我们已知的,因为我们有训练样本,所以在初始化时,我们的线性方程组看起来是如下形式:
y1 = 1 * w1 + 2 * w2 + .... + 3 * wn; .... yn = 3 * w1 + 4 * w2 + .... + 3 * wn;
每个样本代表线性方程组的一行,样本中完全线性共线的可以约去。
这样,我们就得到了一个 N(样本数) * M(特征维度) 的巨大矩阵。而样本的值和标签即(x,y)共同组成了一个巨大的增广矩阵。注意,是样本组成了系数矩阵,不是我们要求的模型参数!
求解线性模型的参数向量(w,b)就是在求解线性方程组的一个方程解,所有的方程解组成的集合称为线性方程组的解集合。
同时,在机器学习中,我们称 w 和 b 为线性模型的超参数,满足等式条件的(w,b)组合可能不只一种,所有的超参数构成了一个最优参数集合。实际上,根据线性方程组的理论,线性方程组要么有唯一解,要么有无限多的解。
唯一解的条件比较苛刻,在大多数的场景和数据集下,解空间都是无限的,机器学习算法的设计目标就是:
基于一种特定的归纳偏置,选择一个特定的超参数(w,b),使得模型具备最好的泛化能力,机器学习算法的目的不是解方程,而是获得最好的泛化能力。
当超参数通过训练拟合过程确定后,模型就得以确定。
0x3:线性模型蕴含的基本思想
线性模型的形式很简单,甚至可以说是一种最简单质朴的模型,但是却蕴含着机器学习中一些重要的基本思想:
1. 原子可叠加性:许多功能更为强大的非线性模型(nonlinear model)可在线性模型的基础上通过引入层级结构或高维映射而得到; 2. 可解释性(comprehensibility):权重向量 w 直观表达了各个属性在预测中的重要性(主要矛盾和次要矛盾),而误差偏置 b 则表达了从物理世界到数据表达中存在的不确定性,即数据不能完整映射物理世界中的所有隐状态,一定存在某些噪声无法通过数据表征出来;
Relevant Link:
https://www.cnblogs.com/jasonfreak/p/5551544.html https://www.cnblogs.com/jasonfreak/p/5554407.html http://www.cnblogs.com/jasonfreak/p/5595074.html https://www.cnblogs.com/pengyingzhi/p/5383801.html
2. 线性回归 - 基于线性模型的一种回归预测模型
0x1:线性回归模型的基本形式
通常给定数据集:D={(x1,y1),(x2,y2),…,(xn,yn)},其中xi=(xi1;xi2;…;xid),yi∈R。
线性回归(linear regression)试图学得一个线性模型:
![]() ,以尽可能准确地预测实值输出标记。
,以尽可能准确地预测实值输出标记。
注意,这里用”尽可能地准确“这个词,是因为在大多数时候,我们是无法得到一个完美拟合所有样本数据的线性方程的,即直接基于输入数据构建的多元线性方程组在大多数时候是无解的。
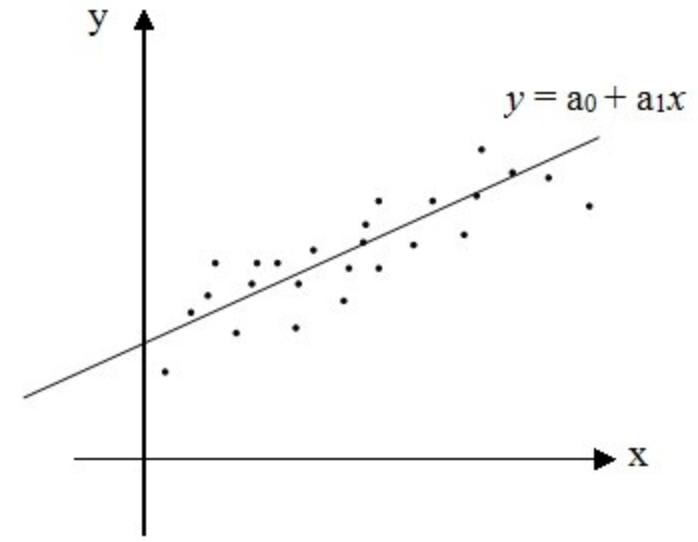
例如下图,我们无法找到一条完美的直线,刚好穿过所有的数据点:
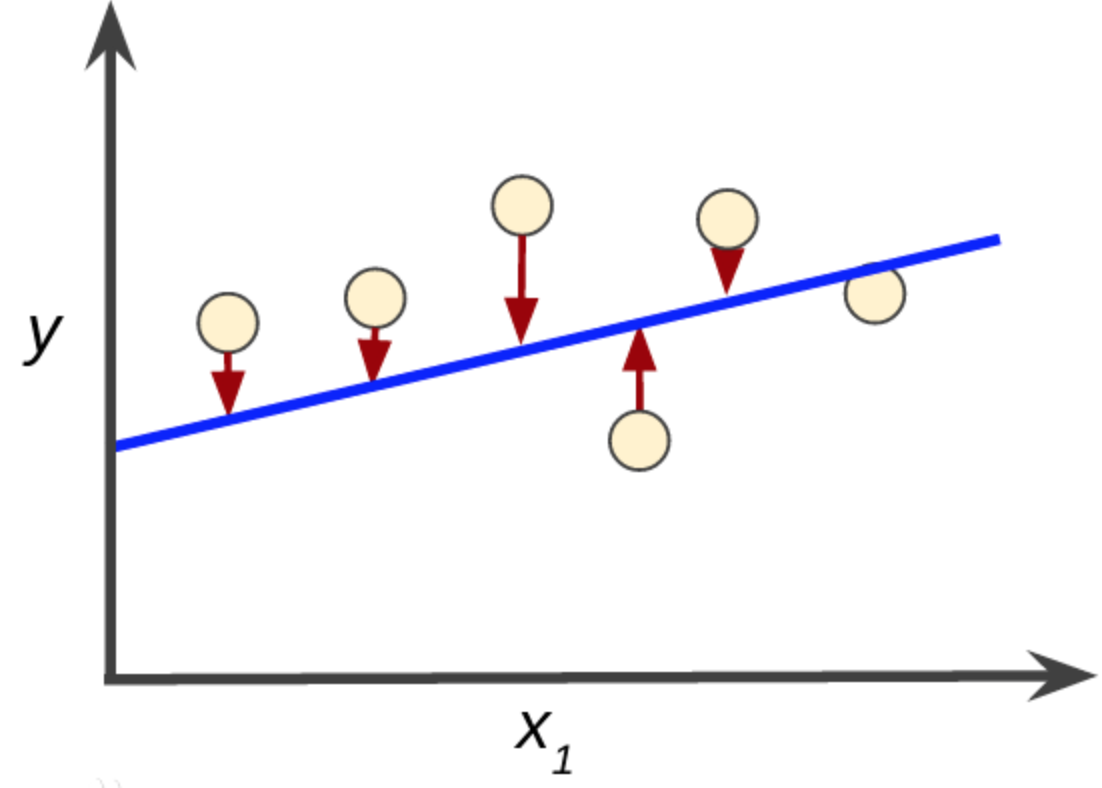
这个时候怎么办呢?数学家高斯发现了最小二乘,它的主要思想是:寻找一个解向量,它和目标数据点的距离尽可能地小。
所以现代线性回归算法所做的事情是:在一定的线性约束条件下,求解线性目标函数的极值问题,这是一个线性规划问题。
0x2:线性回归模型中损失函数的选择
我们上一章说道,直接基于输入数据求解对应线性方程组是无解的,高斯为了解决这个问题,引入了最小二乘。在此之上,之后的数学家又发展出了多种损失评估函数,其数学形式各异,但其核心思想是一致的。
我们知道,损失函数的选择,本质上就是在选择一种误差评价标准。我们知道,损失函数的本质是物理世界和数学公式之间的桥梁,选择何种损失函数取决于我们如何看待我们的问题场景,以及我们希望得到什么样的解释。关于损失函数的讨论,读者朋友可以参阅另一篇blog。
我们这章来讨论主要的常用损失函数。
1. 最小二乘损失函数
1)线性最小二乘的基本公式
 ,
,  ,
,
2)为什么是最小二乘?不是最小三乘或者四乘呢?
这节我们来讨论一个问题,为什么MSE的形式是平方形式的,这背后的原理是什么。
这里先抛出结论:在假设误差符合大数定理正态分布前提假设下,解线性模型参数优化问题等同于均方误差损失函数最小化问题。
下面来证明这个结论:
在线性回归问题中,假设模型为![]() ,其中 x 为输入,b为偏置项。
,其中 x 为输入,b为偏置项。
根据中心极限定理(注意这个前提假设非常重要)(关于大数定理的相关讨论,可以参阅我另一篇blog)假设模型 h(θ) 与实际值 y 误差 ϵ 服从正态分布(即噪声符合高斯分布),即:
![]()
则根据输入样本 xi 可以计算出误差 ϵi 的概率为:
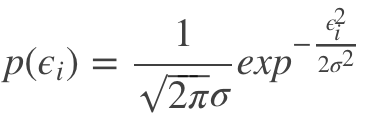
对应似然公式为:
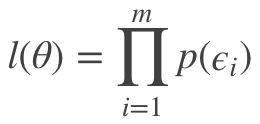
其中 m 为样本总数。基于以上公式可以写出对数最大似然,即对 <span id="MathJax-Span-207" class="mrow"><span id="MathJax-Span-208" class="mi">l<span id="MathJax-Span-209" class="mo">(<span id="MathJax-Span-210" class="mi">θ<span id="MathJax-Span-211" class="mo">) <span class="MJX_Assistive_MathML">整体取log,则:
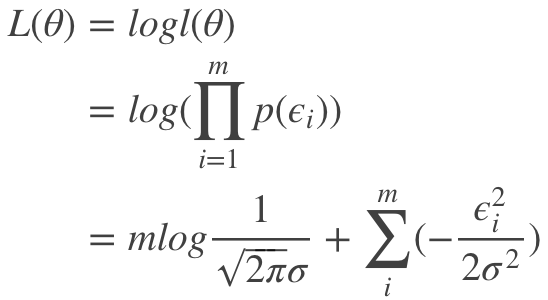
则最大化似然公式 <span id="MathJax-Span-298" class="mrow"><span id="MathJax-Span-299" class="mi">L<span id="MathJax-Span-300" class="mo">(<span id="MathJax-Span-301" class="mi">θ<span id="MathJax-Span-302" class="mo">) <span class="MJX_Assistive_MathML">相当于最小化<img src="https://img2018.cnblogs.com/blog/532548/201903/532548-20190309163133996-1588293181.png" alt="" width="285" height="25" />,<strong>损失函数最小问题</strong>即变换为<strong>最小二乘求解问题</strong>。
另外一点需要注意的是,线性回归的模型假设,这是最小二乘方法的优越性前提,否则不能推出最小二乘是最佳(即方差最小)的无偏估计,具体请参考高斯-马尔科夫定理。特别地,当随机噪声服从正态分布时,最小二乘与最大似然等价。
3)最小二乘参数求解方法
3.1)偏导数为零求极值方法
线性模型试图学得![]() 。同时在噪声符合高斯分布的假设前提下,均方误差是衡量 f(x) 和 y 之间的差别的最佳损失函数。
。同时在噪声符合高斯分布的假设前提下,均方误差是衡量 f(x) 和 y 之间的差别的最佳损失函数。
因此我们可以试图让均方误差最小化,即:

均方误差有非常好的几何意义,它对应了常用的欧几里得距离或简称欧氏距离(enclidean distance)。基于均方误差误差最小化来进行模型求解的方法称为“最小二乘法(least square method)”。
在一元线性回归中,最小二乘法就是试图找到一条直线,使所有样本到直线上的欧氏距离之和最小。
求解 w 和 b 使![]() 最小化的过程,称为线性回归模型的最小二乘参数估计(parameter estimation)。我们可将
最小化的过程,称为线性回归模型的最小二乘参数估计(parameter estimation)。我们可将![]() 分别对 w 和 b 求导,得到:
分别对 w 和 b 求导,得到:
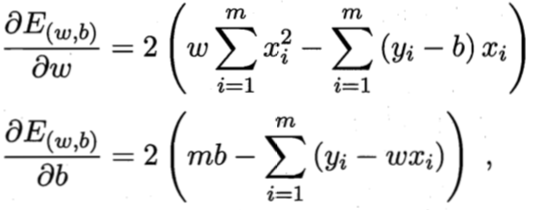
令上式等于零可得到 w 和 b 最优解的闭式(closed-form)解,同时损失函数中极值就是上式参数优化公式的最小值,线性规划问题得解。
注意:这里 E(w,b) 是关于 w 和 b 的凸函数,当它关于 w 和 b 的导数均为零时,得到 w 和 b 的最优解。
但是对于更高维的线性模型甚至非线性模型,目标函数往往并不是全局凸函数,因此不能继续使用导数为零的方式进行最优解求解,这个时候就需要例如GD这种递归优化求解算法。
Relevant Link:
https://www.zhihu.com/question/20822481 https://www.jianshu.com/p/985aff037938 https://juejin.im/entry/5be53a575188257cf9715723
3.2)逆矩阵计算参数求解方法
根据最小二乘求解公式,我们有:
![]()
令![]() ,对
,对![]() 求导得到:
求导得到:![]()
令上式为零可得![]() 最优解的闭式解。
最优解的闭式解。
接下来的问题就是,该线性方程组矩阵是否有解?如果有解,是有唯一解还是有无穷多解?这个问题在矩阵论中有明确的理论定义和讨论,读者朋友可以参阅一些清华/北大初版的线性代数书籍,讲解特别好。
1)满秩情况下
当![]() 为满秩矩阵(full-rank matrix)或正定矩阵(positive definite matrix)时,令上面求导公式为零可得:
为满秩矩阵(full-rank matrix)或正定矩阵(positive definite matrix)时,令上面求导公式为零可得:
![]()
其中,![]() 是矩阵
是矩阵![]() 的逆矩阵,令
的逆矩阵,令![]() ,则最终学得的多元线性回归模型为:
,则最终学得的多元线性回归模型为:
![]()
2)非满秩情况下
然而,在现实中,![]() 往往不是满秩矩阵。
往往不是满秩矩阵。
例如在许多任务中我们遇到大量的变量(即特征维度),其数目甚至超过样例数,导致 X 的列数多于行数,![]() 显然不满秩。此时可解出无限多个
显然不满秩。此时可解出无限多个![]() ,它们都能使均方误差最小化。
,它们都能使均方误差最小化。
选择哪一个解作为输出,将由学习算法的归纳偏好来决定,一个常用的做法是引入正则化(regularization)项。
笔者思考:
线性方程组的行数就是样本数吗?
答案是否定的,准确来说,线性方程组的行数应该是互相线性不相关的样例的行数。因为可以把同一个向量复制N遍,得到N+1个样本,例如(1,1)、(2,2)、(3,3)其实是同一个样例。这里背后其实是矩阵的秩的概念原理。
过拟合和线性方程组求解的关系是什么?
这提示我们可以从线性方程组角度解释过拟合问题的原因。过拟合的问题本质上是方程组的解有无穷多个,而算法模型选择了其中较为复杂的一种。
我们将训练样例输入模型,转化为一个线性方程组,如果从线性方程组化简化阶梯矩阵后,非零行数 < 未知量个数的角度,则该线性方程组有无穷多个解,即有可能发生过拟合。
发生过拟合并不是算法有问题,算法做的就是是合理的,符合现行方程组原理的,其实在解空间中,所有的解都是一样的,都可以使得在这个训练集上的损失最小,但是机器学习的目的是得到一个泛化能力好的模型,而根据奥卡姆剃刀原理,越简单的模型在未知的样本上的泛化能力越好。解决过拟合问题是一个机器学习的技巧,并不是线性代数的数学问题。
关于过拟合问题的详细讨论,可以参阅另一篇blog。
Relevant Link:
https://zhuanlan.zhihu.com/p/34842727 https://zhuanlan.zhihu.com/p/33899560 https://blog.csdn.net/shiyongraow/article/details/77587045
3.3)梯度下降算法(Gradient decent)来求解线性回归模型参数
我们前面说过,为了解决基于原始输入样本数据构成的线性方程组无解的问题,我们引入了损失函数,之后问题转换为了求解损失函数的参数解。
需要明白的,线性模型无论多复杂其本质上都是凸函数,凸函数一定可以求得全局最优的极值点,也即最优参数。
但是,当函数复杂度继续提高,例如增加了非线性变换之后的复合函数之后,目标函数不一定就是凸函数了(例如深度神经网络),这个时候我们就很难直接求得闭式解,矩阵求逆也不一定可以完成。
针对这种复杂函数,GD梯度下降就是一种相对万能通用的迭代式参数求解算法。
当然,理论上,我们也可以将GD算法用于线性模式的参数求解中。
下面的代码中,我们通过GD算法来求解一个二元线性模型的参数,并且将GD的求解结果和使用LSM算法求解的结果进行对比。
首先用3D绘制出数据集的分布:
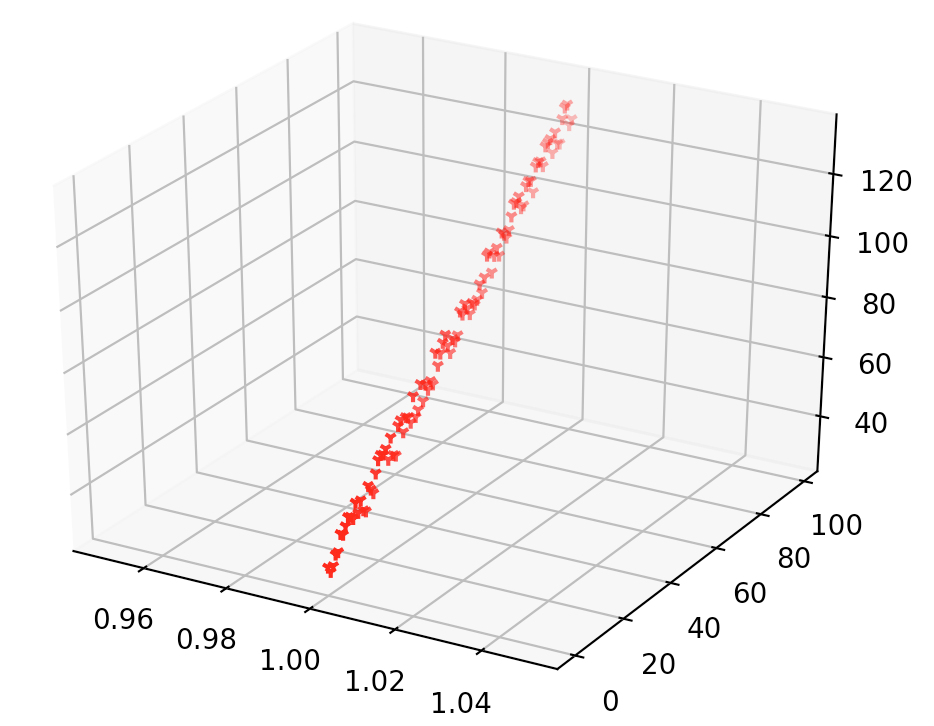
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import random
from sklearn import linear_model
#首先要生成一系列数据,三个参数分别是要生成数据的样本数,数据的偏差,以及数据的方差
def getdata(samples, bias, variance):
X = np.zeros(shape=(samples, 2)) #初始化X
Y = np.zeros(shape=samples)
for i in range(samples):
X[i][0] = 2 * i
X[i][1] = i
Y[i] = (i + bias) + random.uniform(0, 1) * variance
return X, Y
# 梯度下降算法来解决最优化问题,求损失函数的最小值
def gradient(X, Y, alpha, m, iter_numbers):
theta = np.ones(2) # 初始化theta的值 初始化要求解模型中参数的值
bias = np.ones(1)
X_trans=X.transpose() # 转化为列向量
for i in range(iter_numbers):
Y_hat = np.dot(X, theta) + bias # 待预测的函数: y = wx + b
loss = Y_hat - Y # 得到的仍然是一个m*1的列向量
coss = np.sum(loss**2) / (2 * m) # 平方和损失函数
print("iteration:%d / Cost:%f"%(i, coss)) #打印出每一次迭代的损失函数值,正常情况下得到的损失函数随着迭代次数的增加该损失函数值会逐渐减少
gradient_theta = np.dot(X_trans, loss) / m #损失函数的对 theta 参数求导后的结果,后面梯度下降算法更新参数theta的值时会用到这一项的值
gradient_bias = np.sum(loss) / m #损失函数的对 b 参数求导后的结果
theta = theta - alpha * gradient_theta
bias = bias - alpha * gradient_bias
return theta, bias
if __name__=="__main__":
m = 100
X, Y = getdata(m, 25, 10)
# Plot data
ax = plt.subplot(111, projection='3d')
ax.scatter(X[:,0], X[:,1], Y, c='r',marker='1')
theta, bias = gradient(X, Y, 0.00002, m, 2000000)
print("GD -> the parameters (theta) is: ", theta)
print("GD -> the parameters (bias) is: ", bias)
# 打印GD得到的参数对应的函数曲线
X_GD = np.zeros(shape=(m, 2))
Y_GD = np.zeros(shape=m)
for i in range(m):
X_GD[i][0] = 2 * i
X_GD[i][1] = i
Y_GD[i] = theta[0] * X_GD[i][0] + theta[1] * X_GD[i][1] + bias
ax.plot(X_GD[:,0], X_GD[:,1], Y_GD, c='b', lw=1)
clf = linear_model.LinearRegression()
clf.fit(X,Y)
print("LSM -> the theta is: ", clf.coef_)
print("LSM -> the bias is: ", clf.intercept_)
# 打印MSE得到的参数对应的函数曲线
X_LSM = np.zeros(shape=(m, 2))
Y_LSM = np.zeros(shape=m)
for i in range(m):
X_LSM[i][0] = 2 * i
X_LSM[i][1] = i
Y_LSM[i] = theta[0] * X_LSM[i][0] + theta[1] * X_LSM[i][1] + bias
ax.plot(X_LSM[:,0], X_LSM[:,1], Y_LSM, c='g')
plt.show()
运行结果如下:
('GD -> the parameters (theta) is: ', array([0.2020337 , 0.60101685]))
('GD -> the parameters (bias) is: ', array([29.915184]))
('LSM -> the theta is: ', array([0.40202688, 0.20101344]))
('LSM -> the bias is: ', 29.916313760692574)
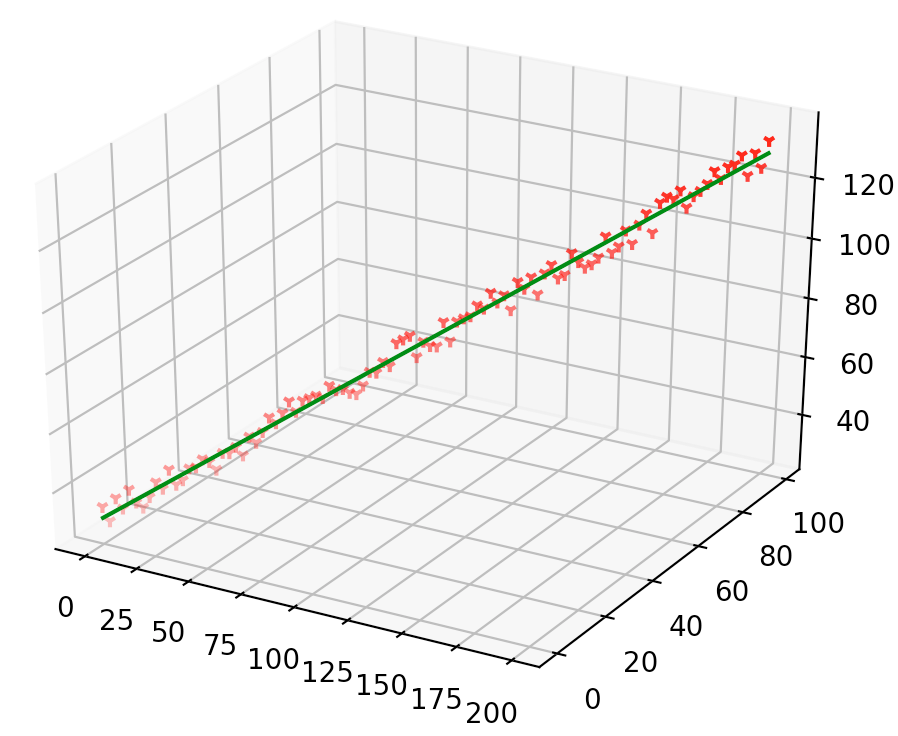
从运行结果以及我们将GD和LSM得到的参数打印出轨迹图中我们可以看出以下几点:
1. 尽管使用了相同的损失函数,但是GD算法得到的结果和LSM最小二乘法的最优结果并不一致,GD算法只是在逼近最优值,且接近最优值,并不能在有限步骤内完全达到最优点;
2. GD算法是一种参数求解算法,和使用什么损失函数没有关系,笔者在代码中使用了MSE平方和损失误差,读者朋友可以自己换成交叉熵代价损失,并不影响最终结果。
3. 在梯度下降中,权值更新是一个迭代的过程,每个维度权值(wi)更新取决于当前轮次中的误差,误差较大大的个体(xi)会使得对应的 wi 调整的更剧烈,这点从代码中可以体现。这种权值更新办法比较直观,但是同时也比较低效:即人人都有发言的权利,每次只考虑部分人,容易顾此失彼。
相比之下,LSM直接基于大数定理进行最小化均方误差,本质上就是求每个属性维度 xi 的样本均值。
3.4)其他参数优化算法
最速下降法是一种最优化求极值的方法。与此相关的还有共轭梯度法,牛顿法,拟牛顿法(为解决海森矩阵求逆代价过大的问题)等。
笔者思考:最小二乘和GD都需要计算 w 和 b 的偏导数。但是不同的的是,最小二乘直接基于偏导数求极值求得最全最优的参数值,而GD基于偏导数作为本轮迭代对 w 和 b 的修正因子(梯度方向)。
Relevant Link:
https://blog.csdn.net/Wang_Da_Yang/article/details/78594309
4)最小二乘损失的几何意义
这个章节,我们来讨论下几何投影与最小二乘法的联系。线性代数中的非常多概念都能在三维空间中找到对应的概念,这非常有利于我们学习和理解。
最小二乘法中的几何意义是:高维空间中的一个向量在低维子空间的投影。这个思想在MIT教授Gilbert Strang的线性代数的公开课程上有讨论。
我们基本向量讨论概念开始讨论起:
3.1)三维空间的向量在二维平面的投影
我们以三维空间作为例子,因为三维是可视化的最高维度,同时更高维的情况是可以扩展的。
如下图所示,在三维空间中给定一个向量 u,以及由向量 v1,v2 构成的一个二维平面:
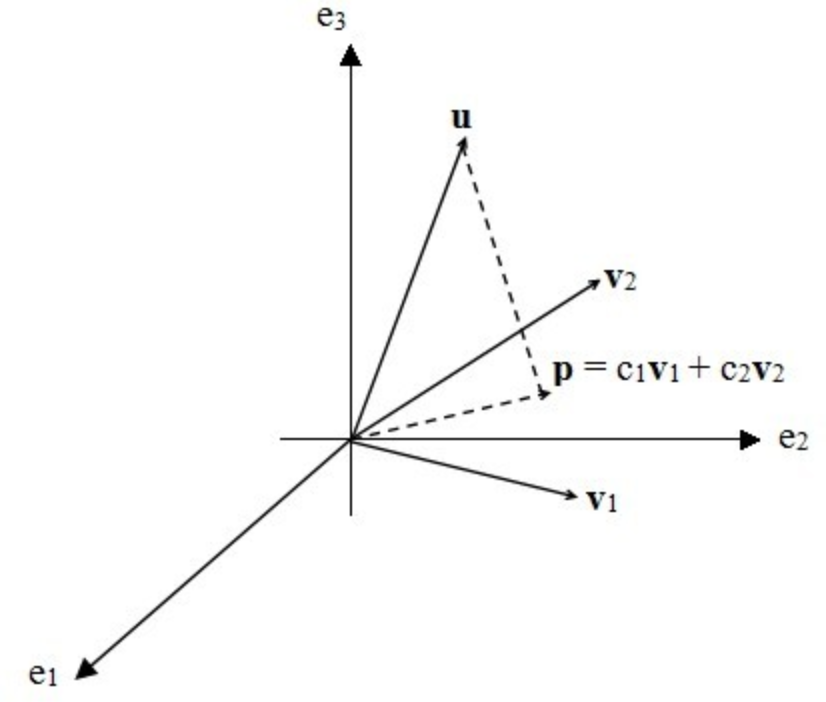
向量 p 为 u 到这个平面的投影,它是 v1,v2 的线性组合:
![]()
接下来我们利用 u - P 这个向量分别与 v1,v2 垂直这两个条件,分别能求出 c1,c2。用数学语言来表示,就是下面这两个式子。
![]()
为了方便之后扩展到更高维的情况,我们把它们合并成一个式子,令 V = [v1,v2],则上式等价于:
![]()
把向量p公式带入上式,然后矩阵转置(transpose)一下,得到以下这个式子
![]()
这里的 c = [c1,c2]T。所以系数 c 的表达式为
![]()
3.2)最小二乘和投影的关系
以二元情况为例,![]()
每个点的误差可以写成:![]()
损失函数的目标是最小化误差的平方和,也就是下面这个关于 a0,a1 的函数(注意,xi,yi都是已知的输入数据):
![]()
这是个函数求极值的问题,我们很快想到可以矩阵微分求导来得到答案:
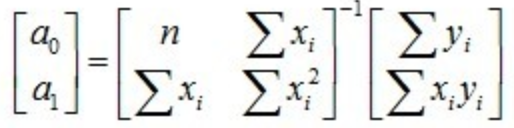
现在我们把平方和损失S重新写成矩阵形式,平方和损失就是下面这个向量的长度平方:
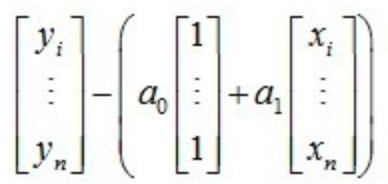
把上面呢这个向量长度最小化的意思是:寻找在 [1, ... , 1]T 和 [x1, ... , xn]T 构成的二维子空间上的一个点,使得向量 [y1, ... , yn]T 到这个点的距离最小。
那怎么找这个点呢?根据几何原理,只要做一个几何投影就好了。
我们只要把上个小节中的几何投影公式中的 u 替换成 [y1, ... , yn]T ,把 v1,v2 分别替换成 [1, ... , 1]T 和 [x1, ... , xn]T, 系数 c1 和 c2 也就是我们要求的 a0,a1,可以马上可以得出:
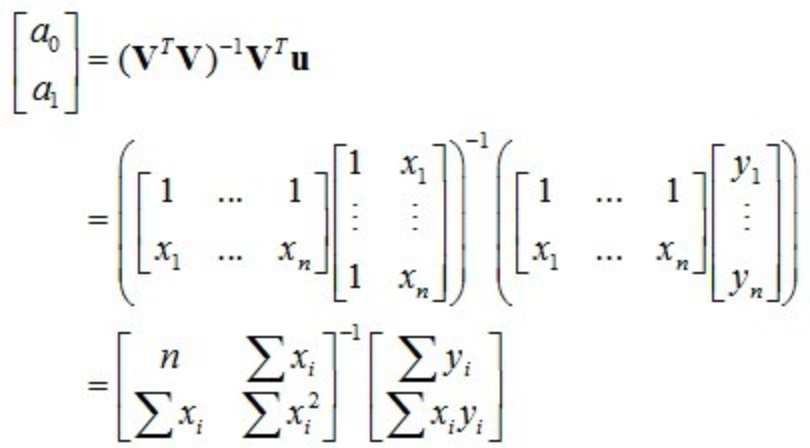
这和用矩阵微积分求得的公式是一样的。
总结一下:最小二乘法的几何意义是高维空间的一个向量(由y数据决定)在低维子空间(由x数据以及多项式的次数决定)的投影。
Relevant Link:
https://www.jianshu.com/p/b49f28b1b98c https://baike.baidu.com/item/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98%E6%B3%95/2522346?fr=aladdin 《线性代数的几何意义》西安电子科技大学出版社 https://blog.csdn.net/xiaoshengforever/article/details/14546075
2. 交叉熵代价函数
从信息熵的角度来看损失误差,在KL散度最小的前提假设下,线性模型参数优化问题等同于交叉熵代价函数最小化问题。
这个章节,我们从熵(Entropy) -> KL散度(Kullback-Leibler Divergence) -> 交叉熵 -> 交叉熵在一定条件下等价于KL散度,这个顺序逐渐引入我们的话题,即:为什么交叉熵代价函数同样适合用作线性模型(实际上不只线性模型)的损失函数,而且效果并不比MSE均方损失函数差,甚至在某些复杂模型场景下(例如深度神经网络模型),交叉熵代价函数的效果和性能还要优于MSE(从函数收敛性质的角度讨论)。
1)熵(Entropy) - 表示一个事件A的自信息量
放在信息论的语境里面来说,就是一个事件所包含的信息量。我们常常听到"这句话信息量好大",比如"昨天花了10万,终于在西湖边上买了套500平的别墅"。这句话为什么信息量大?因为它的内容出乎意料,违反常理。由此引出信息的两个基本规则:
-
越不可能发生的事件信息量越大,比如"上帝存在"这句话信息量就很大。而确定事件的信息量就很低,比如"我是我妈生的",信息量就很低甚至为0。
- 独立事件的信息量可叠加。比如"a. 张三今天喝了阿萨姆红茶,b. 李四前天喝了英式早茶"的信息量就应该恰好等于a+b的信息量,如果张三李四喝什么茶是两个独立事件。
因此熵被定义为  , x指的不同的事件比如喝茶,
, x指的不同的事件比如喝茶, 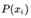 指的是某个事件发生的概率比如和红茶的概率。
指的是某个事件发生的概率比如和红茶的概率。
对于一个一定会发生的事件,其发生概率为1, ,信息量为0;反之,对于一个不可能发生的事,信息量无穷大,这个公式也包含了一个意思,宇宙中不存在完全不可能的事情。
,信息量为0;反之,对于一个不可能发生的事,信息量无穷大,这个公式也包含了一个意思,宇宙中不存在完全不可能的事情。
熵的主要作用是告诉我们最优编码信息方案的理论下界(存储空间),以及度量数据的信息量的一种方式。理解了熵,我们就知道有多少信息蕴含在数据之中。
2)衡量两个事件/分布之间的不同 - KL散度
我们已经知道对于一个随机变量x的事件A的自信息量可以用熵来衡量。但是如果我们有另一个独立的随机变量x相关的事件B,该怎么计算它们之间的区别?或者说我们如何对两个不同的概率分布之间的区别进行定量的分析?
此处我们讨论一种常用的计算方法:KL散度,有时候也叫KL距离,一般被用于计算两个分布之间的不同。
对KL散度,需要重点牢记的是,KL(A||B)散度是有严格的方向性的:KL散度不具备有对称性,A到B的KL散度和B到A的KL散度是不同的。
举个例子:
事件A:张三今天买了2个土鸡蛋,事件B:李四今天买了6个土鸡蛋。
我们定义随机变量x:买土鸡蛋,那么事件A和B的区别是什么?
对于张三来说,李四多买了4个土鸡蛋;对于李四来说,张三少买了4个土鸡蛋。选取的参照物不同,那么得到的结果也不同。
3)KL散度的数学定义
熵公式已经提供了一种量化衡量一个概率分布中包含信息量的多少,只要稍加改造就可以得到两个不同分布之间的信息差异,即 K-L散度。
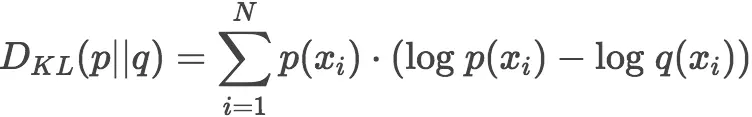
显然,根据上面的公式,K-L散度其实是数据的原始分布 p 和近似分布 q 之间的对数差值的期望。如果用2为底的对数计算,则 K-L散度值表示信息损失的二进制位数。下面公式以期望表达K-L散度:
![]()
一般,K-L散度以下面的书写方式更常见:
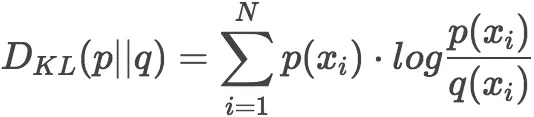
4)k-l散度的数学特性
从公式中可以看出:
- 如果 P(p) = P(q),即两个事件分布完全相同,那么KL散度等于0,当事件A为100%确定性事件时,分子为1,而当事件 q 越接近100%确定(即越靠近事件 p)时,总体KL散度公式趋向于0。
- KL散度公式中,减号左边的和公式事件 p 的熵有关,这是一个非常重要的理解KL散度的视角。
- KL散度是严格顺序的,如果颠倒一下顺序,那么结果就不一样了。所以KL散度来计算两个分布 p 与 q 的时候是不是对称的,有"坐标系"的问题。
5)交叉熵
交叉熵公式:
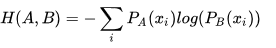
交叉熵的一些性质:
- 和KL散度相同,交叉熵也不具备对称性:
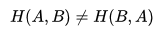 ;
; - Cross(交叉)主要是用于描述这是两个事件之间的相互关系,对自己求交叉熵等于熵。即
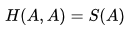 ;
;
6)交叉熵在一定条件下等价于KL散度
观察交叉熵和KL散度的公式可以发现,交叉熵和KL散度的公式非常相近。事实上交叉熵公式就是KL散度的后半部分:![]()
对比一下这是KL散度的公式:
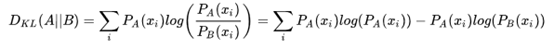
这是熵的公式:
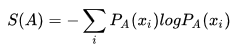
这是交叉熵公式:
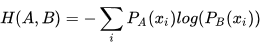
而 S(A) 代表了待估计对象本身的真实分布,它的熵可以被认为是一个常量,因此在求极值的时候,常量可以忽略,也就是说KL散度和交叉熵在真值存在条件下下等价。
在机器学习项目中,我们都可以假设真值是一定存在的,而且分布是固定的。因此我们的损失函数可以直接选择cross-entropy代替kl散度。
7)交叉熵作为损失函数在机器学习中的作用
机器学习的过程就是希望在训练数据上模型学到的分布![]() 和真实数据的分布
和真实数据的分布 ![]() 越接近越好(泛化能力才是机器学习模型的最终目的,注意不是仅仅在训练集上表现好)。怎么衡量并最小化两个分布之间的不同呢?通过使其KL散度最小即可达到目的!
越接近越好(泛化能力才是机器学习模型的最终目的,注意不是仅仅在训练集上表现好)。怎么衡量并最小化两个分布之间的不同呢?通过使其KL散度最小即可达到目的!
但我们没有真实数据的分布,那么只能退而求其次,希望模型学到的分布和训练数据的分布![]() 尽量相同,也就是把训练数据当做模型和真实数据之间的代理人。假设训练数据是从总体中独立同步分布采样(Independent and identically distributed sampled)而来,那么我们可以利用最小化训练数据的经验误差来降低模型的泛化误差。即
尽量相同,也就是把训练数据当做模型和真实数据之间的代理人。假设训练数据是从总体中独立同步分布采样(Independent and identically distributed sampled)而来,那么我们可以利用最小化训练数据的经验误差来降低模型的泛化误差。即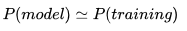 ,我们假设如果模型能够学到训练数据的分布,那么应该近似的学到了真实数据的分布
,我们假设如果模型能够学到训练数据的分布,那么应该近似的学到了真实数据的分布
但是,完美的学到了训练数据分布往往意味着过拟合,因为训练数据不等于真实数据,我们只是假设它们是相似的,而一般还要假设存在一个高斯分布的误差,是模型的泛化误差下限。
Relevant Link:
https://zhuanlan.zhihu.com/p/39682125 https://www.cnblogs.com/kexinxin/p/9858573.html https://blog.csdn.net/qq_17073497/article/details/81485650 https://blog.csdn.net/jiaowosiye/article/details/80786670 https://blog.csdn.net/u014135091/article/details/52027213 https://www.jianshu.com/p/3e163b6b96f5 https://blog.csdn.net/pxhdky/article/details/82388964 https://www.jianshu.com/p/43318a3dc715 https://www.zhihu.com/question/41252833
3. 其他损失函数
除了mse和cross-entropy之外,我们还可以使用例如绝对值损失、0-1损失等损失函数,其本质都是一样的。
3. 对数几率回归 - 基于线性回归的一种概率函数
在实数数域R上,线性模型输出的一个实值,如果我们希望将其用于分类任务,只需要找到一个单调可微函数,将分类任务的真实标记 y 与线性回归模型的预测值联系(link)起来即可。
0x1:阶跃函数 - 硬分类
考虑二分类任务,其输出标记![]() ,而线性回归模型产生的预测值
,而线性回归模型产生的预测值![]() 是实值,于是,我们将实值 z 转换为 0/1 值,一种最简单直观的连接函数是“单位阶跃函数(unit-step function)”。
是实值,于是,我们将实值 z 转换为 0/1 值,一种最简单直观的连接函数是“单位阶跃函数(unit-step function)”。
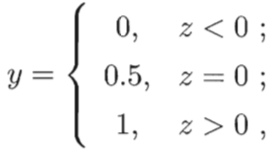
即若预测值 z 大于零就判别为正例;小于零则判别为反例;预测值为临界值则可以任意判别;
这种判别很符合人的直观直觉,实际上在生活中我们面临选择的时候很多时候就是遵循阶跃式的判别思维模式的。
但是,从数学上,单位阶跃函数不连续,无法进行求导,不利于方程组求解。
0x2:sigmoid函数(对数几率函数) - 软分类
对数几率函数(logistic function)在一定程度上近似代替单位阶跃函数,同时具备单调可微的数学性质,非常便于求导。
下图是对数几率函数和单位阶跃函数的对比
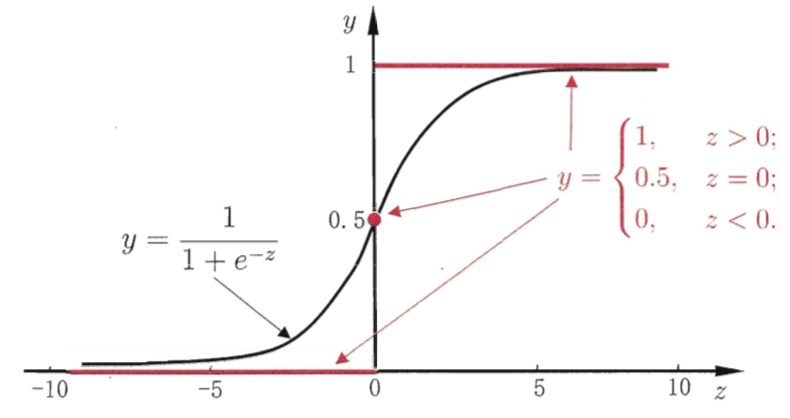
可以看到,对数几率函数是一种“sigmoid函数”,它将 z 值转化为一个接近 0 或 1 的 y 值,并且其输出值在 z = 0 附近变换很陡。
对数几率函数的函数形式如下:
![]() =
= ![]()
1. logistic function中体现的几率性质
对数几率函数的公式可等价变化为:
![]()
在对数几率函数的语境中,我们定义 y 为正例发生的概率,而 1-y 代表了反例发生的概率。两者的比值 y / 1-y 称为“几率(odds)”,反映了 x 作为正例的相对可能性,相对于反例发生的可能性。
对几率函数取对数即得到“对数几率(log odds,即logit)”,即
![]() 。
。
由此可以看到,对数几率实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率。因此,其对应的模型称为“对数几率回归(logistic regression)”,亦称 logit regression。
需要特别注意的是,虽然它的名字是“回归”,但实际却是一种分类学习方法。
0x3:对数几率回归的优点性质
1. 它直接对分类可能性进行建模,是一种判别式模型,无需事先假设数据分布,这样就避免了假设分布不准确所带来的问题; 2. 它不仅是预测出“类别”,而是可得到近似概率预测,这对需要需要利用概率辅助决策的任务很有用; 3. 对数几率函数是任意阶可导的凸函数,有很好的数学性质,现有的许多数值优化算法都可以直接用于求取最优解;
0x4:求解模型参数(w,b)
我们将![]() 视为类后验概率估计
视为类后验概率估计![]() ,则对数几率函数可重写为:
,则对数几率函数可重写为:
![]()
又因为有:
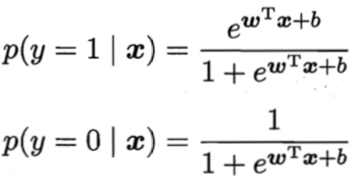
于是,我们可以通过“极大似然法(maximum likelihood method)”来估计(w,b)。
给定数据集![]() ,对数几率回归模型最大化“对数似然(log likelihood)”
,对数几率回归模型最大化“对数似然(log likelihood)”
![]()
即令每个样本属于其真实标记的概率越大越好。
为了便于讨论,令![]() 即参数向量,
即参数向量,![]() 即正例向量,则
即正例向量,则![]() 可简写为
可简写为![]() 。
。
再令![]() ,
,![]() 。
。
则上面对数似然公式中的似然项可重写为:
![]()
综上可得,最大化对数似然函数等价于最小化下式:
![]() ,即
,即![]()
上式是关于![]() 的高阶可导连续函数,根据凸优化理论,经典的数值优化算法,如梯度下降(gradient descent method)、牛顿法(newton method)等都可以求得次最优解。
的高阶可导连续函数,根据凸优化理论,经典的数值优化算法,如梯度下降(gradient descent method)、牛顿法(newton method)等都可以求得次最优解。
Relevant Link:
https://baike.baidu.com/item/%E5%AF%B9%E6%95%B0%E5%87%A0%E7%8E%87%E5%9B%9E%E5%BD%92/23292667?fr=aladdin
4. 广义线性回归
0x1:对数线性回归
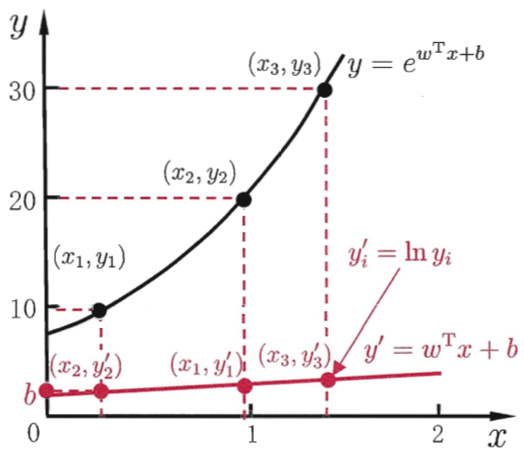
假设我们认为模型所对应的输出标记是在指数尺度上的变化,那就可以将输出标记的对数作为线性模型逼近的目标,即:
![]() 。这就是“对数线性回归(log-linear regression)”
。这就是“对数线性回归(log-linear regression)”
它实际上是在试图让![]() 逼近y。对数线性回归虽然形式上还是线性回归,但实质上已是在求取输入空间到输出空间的非线性函数映射。
逼近y。对数线性回归虽然形式上还是线性回归,但实质上已是在求取输入空间到输出空间的非线性函数映射。
0x2:广义线性模型
更一般地,考虑单调可微函数![]() ,令:
,令:
![]()
这样得到的模型称为“广义线性模式(generalized linear model)”,其中函数![]() 称为“联系函数(link function)”。
称为“联系函数(link function)”。
显然,对数线性回归是广义线性模型在![]() 的特例。
的特例。
Relevant Link:
https://baike.baidu.com/item/%E5%B9%BF%E4%B9%89%E7%BA%BF%E6%80%A7%E6%A8%A1%E5%9E%8B/8465894?fr=aladdin
4. 线性判别分析(Fisher linear discriminant analysis) - 基于线性模型的线性投影判别算法
线性判别分析(linear discriminant analysis LDA)是一种经典的线性学习方法,在二分类问题上最早由Fisher提出,因此亦称为“Fisher判别分析”。
0x1:LDA的思想
LDA的思想非常朴素:
1. 给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离; 2. 在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别;
下图给出了一个二维示意图:
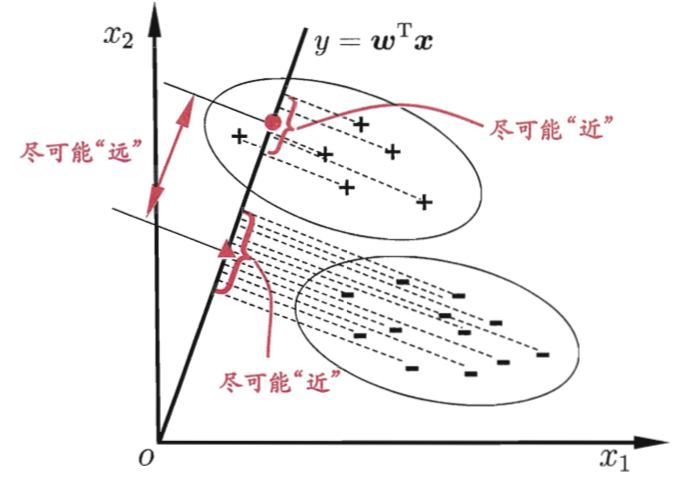
0x2:LDA算法数学公式
给定数据集![]() ,令
,令![]() 表示第
表示第![]() 类示例的集合、
类示例的集合、![]() 表示均值向量、
表示均值向量、![]() 表示协方差矩阵。
表示协方差矩阵。
若将数据投影到直线 w 上,则两类样本的中心在直线上的投影分别为![]() 和
和![]() 。
。
若将所有样本点都投影到直线上,则两类样本的协方差分为为![]() 和
和![]() 。
。
0x3:LDA算法求最优解
欲使同样样例的投影点尽可能接近,可以让同类样例投影点的协方差尽可能小,即![]() +
+![]() 尽可能小;而
尽可能小;而
而欲使异类样例的投影点尽可能远离,可以让类中心之间的距离尽可能大,即![]() 尽可能大。
尽可能大。
同时考虑上述2者,可得最大化的总目标:

定义“类内散度矩阵(within-class scatter matrix)”
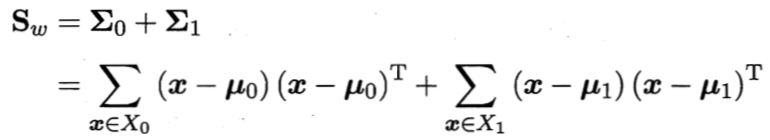
定义“类间散度矩阵(between-class scatter matrix)”
![]()
则上式最大化总目标函数为重写为:
![]()
上式即LDA欲最大化的目标,即转化为最大化 Sb 与 Sw 的“广义瑞利商(generalized Rayleigh quotient)”
接下来的问题是如何求得 w 呢?注意到上式中,分子和分母都是关于 w 的二次项,分子分母中关于w的长度部分会相约,因此解与 w 的长度无关,只与其方向有关,即选择的超曲线w的方向决定了广义瑞利商的值。
不是一般性,令![]() =1,则上式等价于:
=1,则上式等价于:
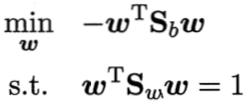
借助拉格朗日乘子法,上式等价于:
![]()
其中 λ 是拉格朗日乘子,注意到![]() 的方向恒为
的方向恒为![]() ,不妨令:
,不妨令:![]()
带入上式得:
![]()
考虑到数值解的稳定性,在实践中通常是对 Sw 进行奇异值分解,即:Sw = ![]() ,这里 ∑ 是一个实对角矩阵,其对角线上的元素是 Sw 的奇异值,然后再由
,这里 ∑ 是一个实对角矩阵,其对角线上的元素是 Sw 的奇异值,然后再由![]() 得到
得到![]() 。
。
0x4:LDA和PCA的内在共通之处
在machine learning领域,PCA和LDA都可以看成是数据降维的一种方式。但是PCA是unsupervised,而LDA是supervised。
所以PCA和LDA虽然都用到数据降维的思想,但是监督方式不一样,目的也不一样。
PCA是为了去除原始数据集中冗余的维度,让投影子空间的各个维度的方差尽可能大,也就是熵尽可能大;LDA是通过数据降维找到那些具有discriminative的维度,使得原始数据在这些维度上的投影,不同类别尽可能区分开来,而同类别之间尽量相近。
显然,这2种算法内核都借助方差矩阵实现最优化算法,从而实现数据降维压缩的目的。另一方面,笔者个人认为LDA的算法思想和一些社区发现算法例如pylouvain倒是有异曲同工之妙。
Relevant Link:
https://www.cnblogs.com/jiahuaking/p/3938541.html https://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html
5. 类别不平衡问题,及其缓解手段
0x1:类别不平衡带来的“伪训练成功问题”
我们本文讨论的分类方法都有一个共同的假设,即不同类别的训练样本数量相当。如果不同类别的训练样本数目稍微有区别,通常影响不大,但若差别很大,则会对学习过程造成困扰,甚至得到一个伪成功的结果。
例如有998个反例,但正例只有2个,那么学习方法只需返回一个永远将新样本预测为反例的学习器,就能达到99.8%的精度,这样的学习器往往泛化能力很差,因为它不能预测出任何正例。
读者朋友可能会质疑机器学习模型不可能这么笨,但其实是确认可能发生,例如GD在优化过程中,有一个局部最优点(全部预测为反例)以及一个全局最优点(998反例,2个正例),但是因为训练参数设置的关系,GD可能就会陷入那个局部最优,而永远跳不出来。
这就是类别不平衡问题(class-imbalance),指分类任务中不同类别的训练样例数目差别很大的情况。
0x2:类别不平衡带来的影响的原理分析
从对数概率线性回归分类器的角度讨论容易理解,在我们用![]() 对新样本 x 进行分类时,事实上是在用预测出的 y 值与一个阈值进行比较。
对新样本 x 进行分类时,事实上是在用预测出的 y 值与一个阈值进行比较。
例如通常在 y > 0.5(1-y < 0.5)时判别为正例,否则为反例。
y 实际上表达了正例的可能性,几率 y/1-y 在反映了正例可能性和反例可能性的比值,阈值设置为0.5恰表明了分类器认为真实正、反例可能性相同,即分类器决策规则为:
若 y/1-y > 1:预测为正例.
然而,当训练集中正、反例数目不同时,令![]() 表示正例数目,
表示正例数目,![]() 表示反例数目,则观测几率是
表示反例数目,则观测几率是![]() 。
。
由于我们通常假设训练集是真实样本总体的无偏采样,因此观测几率就代表了真实几率。注意这个非常重要的大前提,只有这个大前提成立,类别不平衡问题才存在,否则本小节也没有讨论的必要了,也不需要做任何的缩放处理。
于是,理论上来说,预测的阈值应该随着观测样本的类别分布来动态调整,即:
若![]() :预测为正例.
:预测为正例.
但是,我们的分类器逻辑往往是固定的,即“若 y/1-y > 1:预测为正例”。
这就导致实际预测值和理论预测值之间存在一个gap,具体gap的多少取决于类别不平衡的程度:
gap = (1 - y/1-y) * ![]()
当反例和正例差别越大的时候,这个gap的也越大。
0x3:类别不平衡问题的一种解决策略 - 再缩放(rescaling)
正确的做法应该是,需要对预测值进行动态缩放,即:
![]()
如果正反例数目相当,这个再缩放基本可以忽略,如果正反例数目有偏差,这个再缩放可以起到
这就是类别不平衡学习的一个基本策略,“再缩放(rescaling)”。
再次提醒读者朋友的一点是:再缩放的比例是根据真实样本分布中的比例来决定的,但是真实的分布只有上帝才知道,一种比较实用的获取方法是进行海量采样,通过海量样本并结合一些自己的领域业务经验,相对合理的设定这个缩放因子,根据笔者不多的项目经验来看,往往都可以取得比较好的效果。
0x4:类别不平衡问题的另一种解决策略 - 代价敏感学习(cost-sensitive learning)
在代价敏感学习中,将![]() 用
用![]() 代替,其中:
代替,其中:
cost+是将正例误分为反例的代价:如果更加关注正例别漏报了,就加大cost+惩罚比例;
cost-是将反例误分为正例的代价:如果更加关注反例别分错了,就加大cost-惩罚比例;
0x5:如何利用类别不平衡问题实现特定的分类策略
知道了类别不平衡的原理之后,我们可以在实际项目中有效利用这个特性,得到更加贴近业务的分类器。
例如在笔者所在的网络安全的场景中,对precision的要求往往比recall的要求高,因为虚警带来的对用户的困扰是非常巨大的,在任何时候都应该尽量比较误报。
因此,在设计机器学习模型的时候,可以采取以下策略:
1. 训练集中,有意的将白样本:黑样本的比例设置的比较大,例如 5:1,甚至更大,人为的造成一个类别不平衡偏置,这么做的结果很容易理解,模型判黑的几率会降低,会更倾向于判白,也即降低了误报的几率; 2. 在训练中,进行自定义损失函数,keras/tensorflow中很容易做到这点,将“白判黑损失”人为的增加为“黑判白”的 N 倍,这么做的结果和第一点也是一样的;
Relevant Link:
https://stackoverflow.com/questions/45961428/make-a-custom-loss-function-in-keras


 浙公网安备 33010602011771号
浙公网安备 33010602011771号