《White-Box Transformers via Sparse Rate Reduction》论文学习
一、Introduction
近年来,深度学习在处理大量高维多模态数据方面取得了巨大的实证成功。其中很大一部分成功归功于对数据分布的有效学习,然后将分布转化为简洁的结构化和紧凑的表示形式,这有助于许多下游任务(例如视觉、分类、识别和分割以及生成。为此,已提出和实践了许多模型和方法,每种方法都有其优点和局限性。
在这里,我们对几种流行的方法进行简要介绍,作为我们在这项工作中寻求完整理解和统一的背景。
Transformer模型和自注意力(Transformer models and self-attention)
Transformer是最新流行的用于学习高维结构化数据表示的模型之一,例如文本、图像和其他类型的信号。
在第一个块之后,将每个数据点(例如文本语料库或图像)转换为一组或序列的tokens标记,并以一种介质不可知的方式对标记集进行进一步处理。
Transformer模型的一个基石是所谓的自注意力层,它利用tokens标记序列中的统计相关性来改进tokens标记表示。
Transformer在学习性能良好的紧凑表示方面取得了巨大成功。然而,Transformer网络架构是经验设计的,缺乏严格的数学解释。事实上,注意力层的输出本身有几种竞争的解释。因此,数据分布与Transformer学到的最终表示之间的统计和几何关系在很大程度上仍然是一个神秘的黑盒子。
扩散模型和去噪(Diffusion models and denoising)
扩散模型最近成为学习数据分布的一种流行方法,特别是用于”生成任务(generative tasks)“和高度结构化但难以有效建模的自然图像数据。
扩散模型的核心概念是从高斯噪声分布(或其他标准模板)中采样特征,并迭代地去噪和变形特征分布,直到收敛到原始数据分布。如果将这个过程建模为一步是计算上不可行的,因此通常将其分为多个增量步骤。每个步骤的关键是所谓的评分函数,或者说是“最佳去噪函数”的估计。在实践中,这个函数是使用通用的黑盒深度网络建模的。
扩散模型已经显示出在学习和从数据分布中采样方面的有效性。然而,尽管近期进行了一些努力,它们通常没有建立起初始特征与数据样本之间的清晰对应关系。因此,扩散模型本身并没有提供对数据分布的简洁或可解释的表示。
结构寻求模型和采样降维(Structure-seeking models and rate reduction)
在前两种方法中都是通过使用深度网络解决下游任务(例如分类或生成/抽样)的副产品来隐式构建的。然而,我们也可以直接显式地学习数据分布,作为任务本身的目的。
- 最常见的方法是尝试识别和表示输入数据中的低维结构。这一范式的经典示例包括基于模型的方法,如稀疏编码和字典学习,这些方法促使了早期的深度网络架构的设计和解释。
- 近年来的方法则更多地从无模型的角度出发,通过一个足够信息丰富的预训练任务来学习表示(例如在对比学习中压缩相似和分离不相似的数据,或者在最大编码速率减少方法类别中最大化信息增益)。
与黑盒深度学习方法相比,基于模型和无模型的表示学习方案具有更好的可解释性:
- 首先,它们允许用户明确设计所学表示的期望属性。
- 此外,它们允许用户通过展开表示学习目标的优化策略来构建新的白盒前向深度网络架构,使得构建网络的每一层实现优化算法的迭代。
然而,不幸的是,在这种范式中,如果所需属性的定义狭窄,可能很难在大规模真实数据集上实现良好的实际性能。
主要贡献和本文的概述
在本文中,我们旨在通过更统一的框架来解决这些现有方法的局限性,设计类似transformer的网络架构,从而实现数学可解释性和良好的实际性能。为此,我们提出学习一系列增量映射,以获得输入数据(或其令牌集)的最紧凑和稀疏表示,优化统一的目标函数,即稀疏率降维。映射的目标在下图中进行了说明。
在这个框架内,我们将上述三种看似不相关的方法统一起来,并展示了类似transformer的深度网络层可以自然地从展开迭代优化方案中派生出来,以逐步优化稀疏率降维目标。
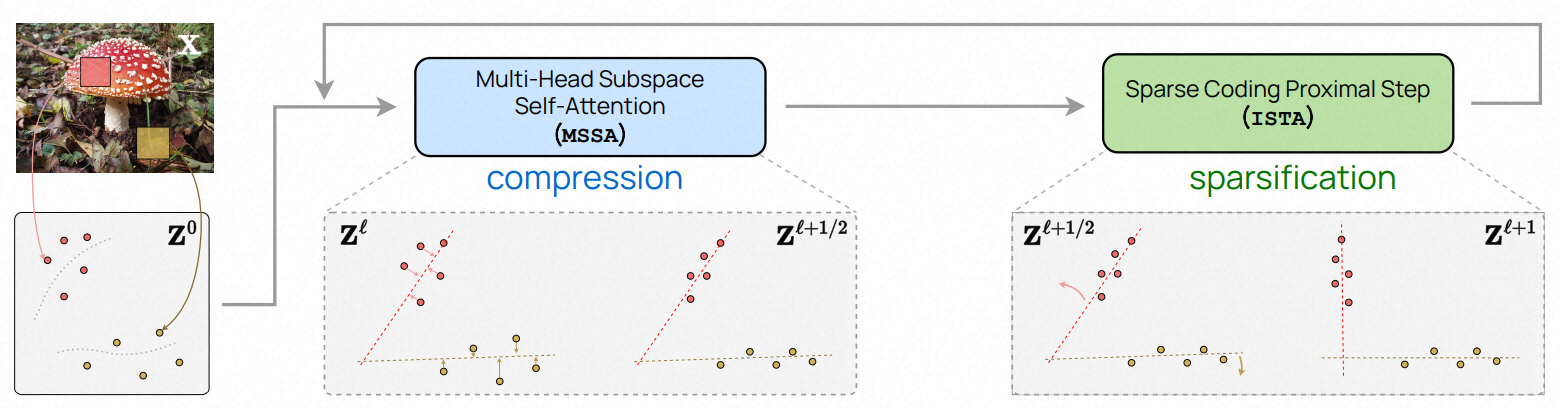
The ‘main loop’ of the CRATE white-box deep network design. After encoding input data X as a sequence of tokens Z0, CRATE constructs a deep network that transforms the data to a canonical configuration of low-dimensional subspaces by successive compression against a local model for the distribution, generating Zℓ+1/2, and sparsification against a global dictionary, generating Zℓ+1. Repeatedly stacking these blocks and training the model parameters via backpropagation yields a powerful and interpretable representation of the data.
具体而言,我们的贡献和本文的概述如下:
- 我们使用一个理想化的令牌分布模型,证明了如果将令牌迭代地向低维子空间去噪声,相关的评分函数会呈现出类似于Transformer中的自注意运算符的显式形式。
- 我们推导出多头自注意层作为一个展开的梯度下降步骤,以最小化有损编码率部分的速率降低,从而展示了自注意层的另一种解释,即对令牌表示进行压缩。
- 我们展示了紧随多头自注意的多层感知器可以被解释为(并被替换为)一个层,通过构建令牌表示的稀疏编码来逐步优化稀疏率降维目标的剩余部分。
- 我们利用这个理解来创建一个新的白盒(完全数学可解释的)Transformer架构,称为CRATE(即Coding RAte reduction TransformEr),其中每个层执行交替最小化算法的单步操作,以优化稀疏率降维目标。
因此,在我们的框架中,学习目标函数、深度学习架构和最终学习到的表示都成为完全数学可解释的白盒。
CRATE网络虽然简单,但已经可以在大规模真实数据集上学习到所需的压缩和稀疏表示,并在各种任务(如分类和迁移学习)上实现与更复杂的Transformer网络(如ViT)相当的性能。
参考链接:
https://ma-lab-berkeley.github.io/CRATE/ https://arxiv.org/pdf/2306.01129.pdf
二、Technical Approach and Justification
0x1:Objective and Approach
我们考虑一个与现实世界信号相关的一般学习任务。
我们有一些随机变量X = [x1, . . . , xN] ∈ RD×N,它是我们的数据来源。每个xi ∈ RD被解释为一个令牌token,xi的相关结构可以是任意的。
我们使用Z = [z1, . . . , zN] ∈ Rd×N来表示定义输入表示的随机变量。每个zi ∈ Rd是相应令牌xi的表示。
我们给出了B ≥ 1 i.i.d.(独立同分布)的样本X1, . . . , XB ∼ X,其令牌为xi,b。
我们样本的表示表示为Z1, . . . , ZB ∼ Z,令牌的表示为zi,b。
最后,对于给定的网络,当输入为X时,我们使用Zℓ来表示前ℓ层的输出。相应地,样本的输出为Ziℓ,令牌的输出为zℓi,b。
1、Objective for learning a structured and compact representation
根据稀疏率降维框架,我们认为表示学习(representation learning)的目标是找到一个特征映射f:
![]()
将具有潜在非线性和多模态分布的输入数据X∈RD×N转换为一个(分段)线性化和紧凑的特征表示Z∈Rd×N。
虽然对应的特征表示Z的联合分布(zi)Ni=1的联合分布可能很复杂(并且任务特定),但我们进一步认为要求单个token标记zi的目标边缘分布应该高度压缩和结构化,便于紧凑编码,这是合理和实用的。
特别地,我们要求该分布是低维(比如K)高斯分布的混合,其中第k个高斯分布的均值为0∈Rd,协方差Σk⪰0∈Rd×d,并且由正交基Uk∈Rd×p组成。
我们用U[K] = (Uk)Kk=1表示所有高斯分布的基集。
因此,为了最大化最终token标记表示的信息增益,我们希望最大化token标记的编码率降低,即:
![]()
![]()
其中R和Rc是损失编码率的估计。
这也促使来自不同高斯分布的标记表示zi不相关。由于编码率降低是表示正例(goodness)的内在度量,它对表示的任意旋转是不变的。因此,为了确保最终的表示适于更紧凑的编码,我们希望将表示(及其支撑子空间)转换为相对于结果表示空间的标准坐标而言是稀疏的。这种结合速率降低和稀疏化的过程在下图中示意。

从计算上讲,我们可以将上述两个目标合并为一个统一的优化目标:
![]()
其中ℓ0范数 ||Z||0提升了最终token标记表示Z = f(X)的稀疏性。
我们将这个目标称为“稀疏编码率降低”。
2、White-box deep architecture as unrolled incremental optimization
虽然很容易陈述,但上述目标的每个术语在计算上都很难优化。因此,自然而然地采用一种近似方法,通过多个简单的增量和局部操作fℓ的连续组合来实现全局转换f优化,从而将表示分布推向期望的简约模型分布。
![]()
其中 f0 : RD → Rd 是将输入token令牌 xi ∈ RD 转换为它们的token令牌表示 z1i ∈ Rd 的预处理映射。
每个增量前向映射 Zℓ+1 = fℓ(Zℓ),或称为“层”,根据其输入token令牌的分布 Zℓ,优化上述稀疏率降维目标函数。
与其他展开优化方法(如ReduNet)不同,我们明确地对每个层的输入分布 Zℓ 进行建模,例如将其建模为线性子空间的混合或由字典稀疏生成。模型参数通过数据学习(例如通过端对端训练进行反向传播)。前向“优化”和后向“学习”的区分明确了每个层作为操作符,转换其输入分布的数学角色,而输入分布则由层的参数建模(并随后学习)。
0x2:Self-Attention via Denoising Tokens Towards Multiple Subspaces
有很多不同的方式可以逐步优化目标函数。在这项工作中,我们提出了可能是最基本的方案。为了帮助澄清我们推导和近似的直觉,在本节中,我们研究了一个在很大程度上理想化的模型,尽管如此,它仍然捕捉到了几乎整个过程的本质,并特别揭示了为什么在许多情况下会出现类似于自注意力的运算符的原因。
假设N = 1,并且单个令牌x是从一个未知的高斯混合![]() 中独立同分布地抽取的,该混合分布在低维子空间上支持具有正交基
中独立同分布地抽取的,该混合分布在低维子空间上支持具有正交基![]() ,并且受到加性高斯噪声
,并且受到加性高斯噪声![]() 的干扰,即:
的干扰,即:
![]()
其中z按照混合分布进行分布。
我们的目标仅仅是将带有噪声的令牌x的分布转化为低维高斯分布的混合。
根据上述增量构建表示f的目标,我们进行归纳推理:如果zℓ 是一个噪声令牌,在噪声水平σℓ 下进行去噪是自然的。从均方意义上讲,最优估计是E[z | zℓ ],它具有变分特征:
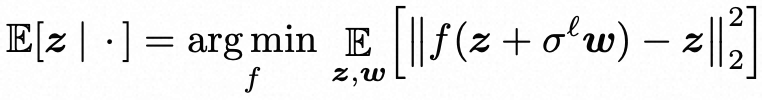
将 zℓ 的下一个阶段表示为 zℓ+1 = E[z | zℓ],因此基于zℓ的局部信号模型,表征了下一个阶段的优化目标。此外,让 x → qℓ(x) 表示 zℓ 的密度,根据Tweedie的公式,我们可以闭式地表示解决上式的最优表达式。
![]()
Tweedie的公式通过噪声观测的对数似然梯度的加性修正(一般为zℓ的非线性函数)来表达最优表示,使得最优表示可以清楚地解释为对当前噪声分布qℓ的递增扰动。这种连接在估计理论和逆问题领域广为人知,并最近在自然图像生成模型的训练中得到了强大的应用。在这里,我们可以计算出这个得分函数![]() 的闭式表达式,当结合上式和一些技术假设时,可以得到以下近似:
的闭式表达式,当结合上式和一些技术假设时,可以得到以下近似:
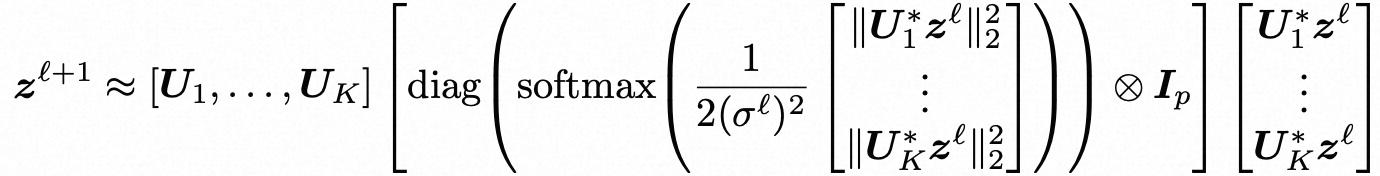
⊗表示Kronecker乘积。
这个操作类似于标准Transformer架构中的自注意力层,具有K个头部,序列长度N = 1,“查询-键-值”结构被单个线性投影![]() 替代,并且头部输出的聚合(通常由MLP建模)由上式中的最左边的两个矩阵完成。
替代,并且头部输出的聚合(通常由MLP建模)由上式中的最左边的两个矩阵完成。
因此,我们得出了以下有用的解释:针对子空间模型的高斯去噪导致了变换f中的自注意力类型层。给定一个遵循模型的初始样本x,我们可以重复使用局部变换与上式中的分布来实现增量映射f:x → z。
这些洞察将指导我们在接下来设计我们的白盒Transformer架构。
0x3:Self-Attention via Compressing Token Sets through Optimizing Rate Reduction
在上一小节中,我们已经看到transformer中的多头注意力机制类似于分数匹配算子,其目标是将一个标记z向量转换为一组子空间(或者退化的高斯分布)。
然而,要对任意数据执行这样的操作,首先需要从有限的样本中学习或估计出这组(退化的)高斯分布的参数,这被认为是一项具有挑战性的任务。因为在典型的学习环境中,给定的标记集并不是从子空间的混合中独立同分布采样得到的。这些标记之间的联合分布可以编码关于数据的丰富信息,例如语言和图像数据中的词语或对象部分的共现关系,我们也应该学习到这些信息。因此,我们应该对这组标记进行压缩/去噪/转换。为了达到这个目的,我们需要一个度量质量的指标,即集合标记的紧凑性。这样一组标记的紧凑性的一个自然度量是将它们编码到一定精度ϵ > 0的(有损)编码率。对于一个零均值的高斯分布,这个度量可以有一个闭合形式。如果我们将 Z ∈ Rd×N 中的标记视为从一个单独的零均值高斯分布中采样得到的,它们的(有损)编码率的估计,受到量化精度ϵ > 0的限制,可以表示为:
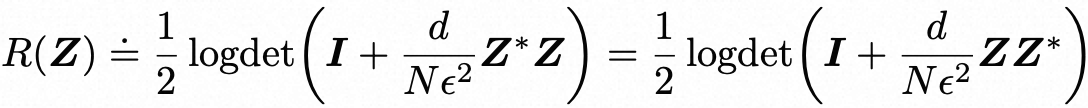
在实践中,数据分布通常是多模态的,例如一个由许多类别组成的图像集,或者很多图像块集合。
更适合的做法是要求令一组标记映射到混合的子空间(退化的高斯分布),我们用![]() 来表示这些子空间的(待学习的)基向量,其中Uk∈Rd×p。
来表示这些子空间的(待学习的)基向量,其中Uk∈Rd×p。
虽然标记Z的联合分布是未知的,但每个标记zi的边际分布是一组子空间的混合。因此,我们可以通过将标记投影到这些子空间上并求得各自的编码率之和来得到标记集Z的编码率的上界。
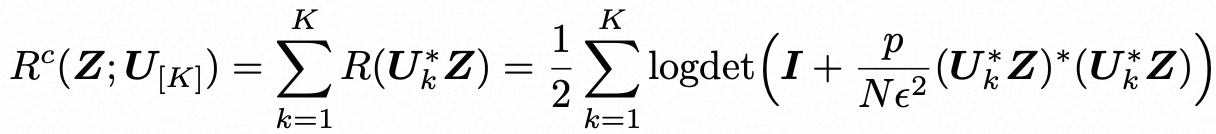
我们希望通过最小化编码率来对这些子空间压缩(或去噪)令牌集。
![]() 的梯度是:
的梯度是:

上述表达式近似了每个投影令牌![]() 由其他令牌
由其他令牌![]() 回归的残差。但是,Z中的不是所有令牌都来自同一个子空间。因此,为了通过自相关来将每个令牌与其所属的组中的令牌去噪,我们可以通过计算它们之间的相似性来将其转化为一个成员分布,即通过softmax计算
回归的残差。但是,Z中的不是所有令牌都来自同一个子空间。因此,为了通过自相关来将每个令牌与其所属的组中的令牌去噪,我们可以通过计算它们之间的相似性来将其转化为一个成员分布,即通过softmax计算![]() 。然后,如果我们只使用相似的令牌来回归和去噪彼此,那么使用学习率 κ 的编码速率的梯度步骤可以自然地近似如下:
。然后,如果我们只使用相似的令牌来回归和去噪彼此,那么使用学习率 κ 的编码速率的梯度步骤可以自然地近似如下:
![]()
其中 MSSA 通过 SSA 运算符定义为:
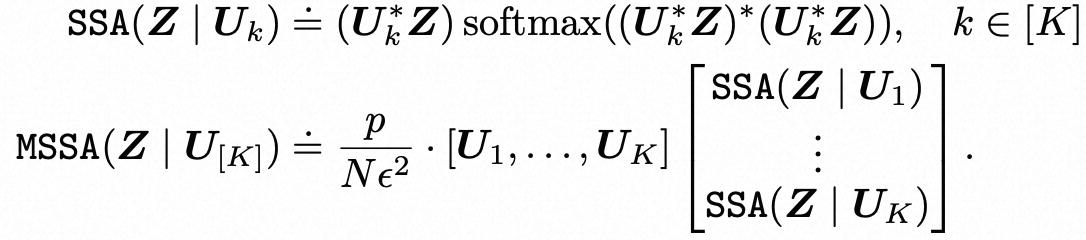
在上式中,SSA运算符类似于典型transformer中的注意力运算符,不同之处在于这里的值、键和查询的线性运算符都被设置为与子空间基础相同,即V = K = Q = U∗k。
因此,我们将![]() 称为子空间自注意力(SSA)运算符。 然后,在上式中定义的整个MSSA运算符,形式上定义为
称为子空间自注意力(SSA)运算符。 然后,在上式中定义的整个MSSA运算符,形式上定义为![]() ,并称为多头子空间自注意力(MSSA)运算符,通过使用与模型相关的权重对注意力头输出进行平均聚合,与现有transformer网络中的流行的多头自注意力运算符类似的概念。整体梯度步骤类似于在transformer中使用跳跃连接实现的多头自注意力。
,并称为多头子空间自注意力(MSSA)运算符,通过使用与模型相关的权重对注意力头输出进行平均聚合,与现有transformer网络中的流行的多头自注意力运算符类似的概念。整体梯度步骤类似于在transformer中使用跳跃连接实现的多头自注意力。
请注意,如果我们有N = 1个标记,以及采取积极的梯度步骤(κ = 1)并调整量化误差(![]() ),则上式中的多头子空间自注意力运算符变成了下式中的理想去噪器,
),则上式中的多头子空间自注意力运算符变成了下式中的理想去噪器,
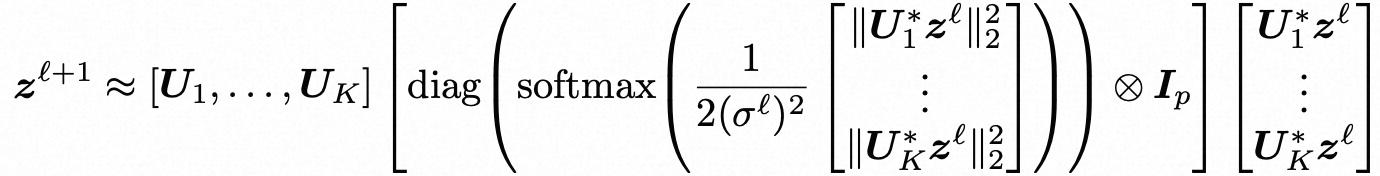
唯一的不同之处在于这里对头部的聚合是通过线性函数完成的,而在上式中则是通过非线性的专家混合类型函数完成的。
这提供了多头自注意力运算符的两个相关解释,作为去噪和针对低维子空间混合的压缩。
0x4:MLP via Iterative Shrinkage-Thresholding Algorithms (ISTA) for Sparse Coding
在前一小节中,我们重点讨论了如何将一组标记与一组(学习到的)低维子空间进行压缩。
优化稀疏率降低目标函数中的剩余项,包括非光滑项,有助于稀疏化压缩的标记,从而导致更紧凑和有结构的(即简洁的)表示。这个项是。

其中,R(Z)表示整个令牌集的编码率,除了通过 ||Z||0项进行稀疏化外,上式中的扩展项R(Z)促进了表示的多样性和非坍缩性,这是非常理想的特性。然而,之前的工作在大规模数据集上难以实现这种好处,因为梯度![]() 的可扩展性较差,需要矩阵求逆。
的可扩展性较差,需要矩阵求逆。
为了简化问题,我们采取了一种不同的方法来权衡表示多样性和稀疏化:我们假设一个(完全)不相干或正交的字典D ∈ Rd×d,并要求对于D对中间迭代Zℓ+1/2进行稀疏化。也就是说,Zℓ+1/2 = DZℓ+1,其中Zℓ+1更加稀疏。字典D是全局的,即用于同时稀疏化所有令牌。根据不相关的假设,我们有![]() ,因此我们有:
,因此我们有:
![]()
![]()
因此,我们用以下程序近似解决上式:
![]()
上述稀疏表示程序通常通过将其放松为一个无约束的凸规划问题来求解,即LASSO。
![]()
在我们的实现中,受到Sun等人和Zarka等人的启发,我们还对Zℓ+1添加了一个非负约束。
![]()
我们通过进行展开的近端梯度下降步骤(也称为ISTA步骤)逐步优化这一部分,得到更新:
![]()
0x5:The Overall White-Box CRATE Architecture
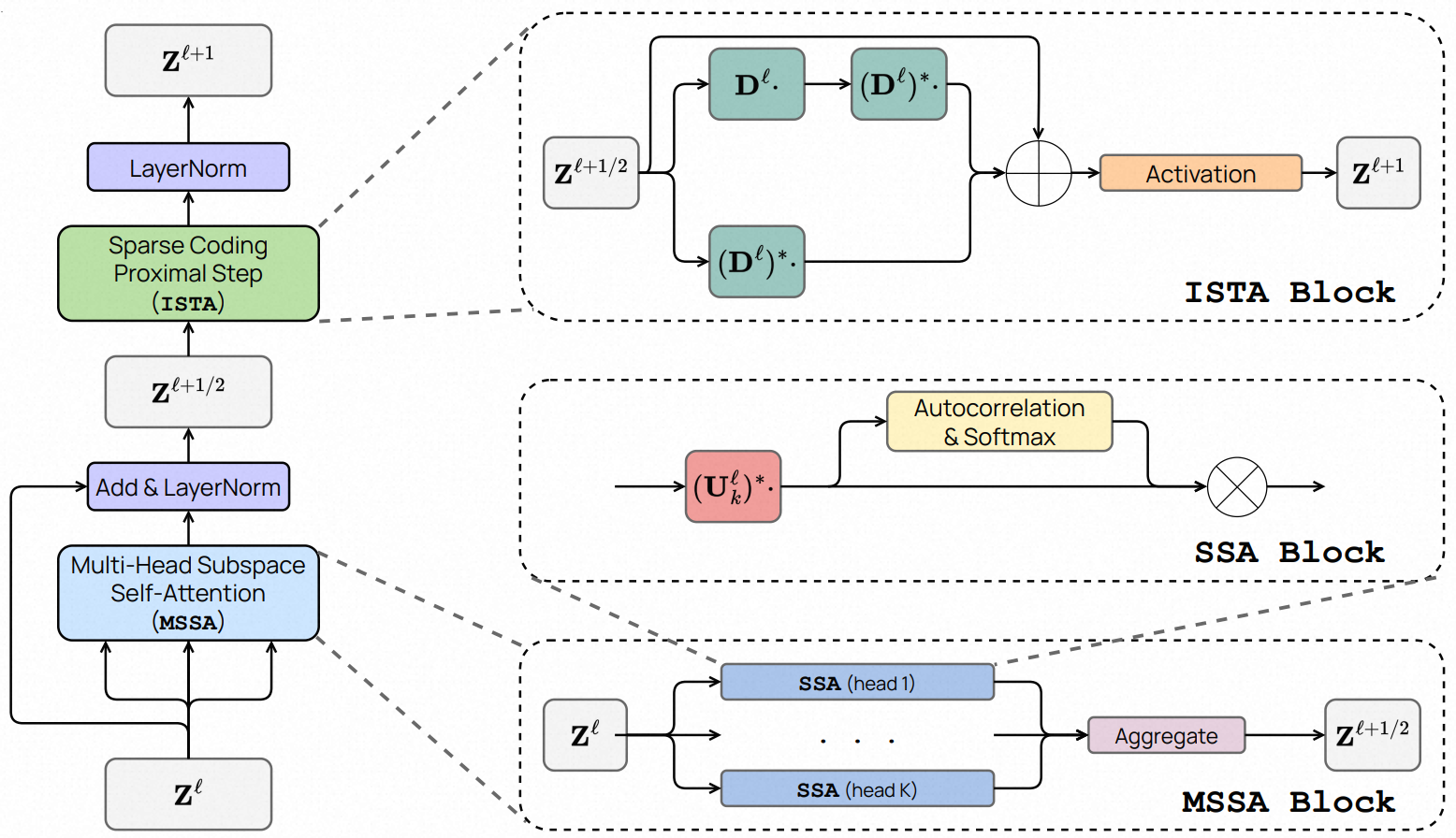
One layer of the CRATE architecture. The full architecture is simply a concatenation of such layers, with some initial tokenizer and final task-specific architecture (i.e., a classification head).
三、Application Experiments
Classification
下面是CRATE用于分类任务的架构。它与流行的vision transformer几乎完全相同。
我们使用软最大交叉熵损失来训练监督图像分类任务。与通常用于分类训练的视觉变换器(ViT)相比,我们获得了具有竞争力的性能,并具有类似的规模行为,包括在ImageNet-1K上超过80%的top-1准确度,而仅使用了ViT参数的25%。
Segmentation and Detection
CRATE的一个有趣现象是,即使在受监督分类训练的情况下,它也学会了对输入图像进行分割,这些分割可以通过注意力图轻松恢复,就像下面的架构流程(类似于DINO)一样。
在以前,只有在像DINO这样的复杂自监督训练机制中,才能看到这种分割方式,然而在CRATE中,分割是监督分类训练的副产品,模型在任何时候都不会获取任何先验分割信息。
接下来,我们展示一些示例分割。

另一个显著的属性是CRATE中的注意力头自动携带语义意义,这意味着CRATE可能具有对其进行的任何分类的事后可解释性。
下面,我们展示了一些注意力头在多张图片和多个动物上的输出,显示一些注意力头对应动物的不同部位。

参考链接:
https://github.com/Ma-Lab-Berkeley/CRATE
四、Conclusion
在本文中,我们提出了一个新的理论框架,可以将deep transformer网络结构推导为逐步优化方案,以学习输入数据(或令牌集合)的压缩和稀疏表示。
所得到和学习的深度架构不仅在数学上是可解释的,而且在每一层上都与其设计目标保持一致。尽管在所有可能的设计中可能是最简单的,但这些网络已经在大规模实际数据集和任务上展示出与老牌变换器接近的性能。
我们相信这项工作真正有助于弥合深度神经网络理论和实践之间的差距,并有助于统一看似独立的学习和表示数据分布的方法。
对于从业者而言,我们的框架为设计和证明新的、潜在更强大的深度架构提供了理论指导。
五、代码示例
ImageNet Dataset prepare
git clone https://github.com/Ma-Lab-Berkeley/CRATE.git cd CRATE/ screen wget https://image-net.org/data/ILSVRC/2012/ILSVRC2012_img_train.tar --no-check-certificate && wget https://image-net.org/data/ILSVRC/2012/ILSVRC2012_img_val.tar --no-check-certificate mkdir imagenet mkdir imagenet/train && mv ILSVRC2012_img_train.tar imagenet/train/ && cd imagenet/train tar -xvf ILSVRC2012_img_train.tar && rm -f ILSVRC2012_img_train.tar find . -name "*.tar" | while read NAME ; do mkdir -p "${NAME%.tar}"; tar -xvf "${NAME}" -C "${NAME%.tar}"; rm -f "${NAME}"; done cd ../.. mkdir imagenet/val && mv ILSVRC2012_img_val.tar imagenet/val/ && cd imagenet/val && tar -xvf ILSVRC2012_img_val.tar && rm -f ILSVRC2012_img_val.tar wget -qO- https://raw.githubusercontent.com/soumith/imagenetloader.torch/master/valprep.sh | bash

Training CRATE on ImageNet
screen python3 main.py --arch CRATE_tiny --batch-size 512 --epochs 200 --optimizer Lion --lr 0.0002 --weight-decay 0.05 --print-freq 25 --data /data_vdb1/CRATE/imagenet

Finetuning pretrained / training random initialized CRATE on CIFAR10
cd CRATE/ python3 finetune.py --bs 256 --net CRATE_tiny --opt adamW --lr 5e-5 --n_epochs 200 --randomaug 1 --data cifar10 --ckpt_dir /data_vdb1/CRATE/checkpoints --data_dir /data_vdb1/CRATE/imagenet
参考链接:
https://www.kaggle.com/competitions/imagenet-object-localization-challenge/data https://cloud.google.com/tpu/docs/imagenet-setup?hl=zh-cn https://github.com/pytorch/examples/blob/main/imagenet/extract_ILSVRC.sh https://stackoverflow.com/questions/64714119/valid-url-for-downloading-imagenet-dataset




 浙公网安备 33010602011771号
浙公网安备 33010602011771号