P6429 [COCI2008-2009#1] JEZ 题解
题目传送门:Click。
更好地观感:Click(进入速度玄学)
某蒟蒻看见这道题,想了足足一个晚上,过后茅塞顿开,故作此篇。
感谢神犇的题解,思路基本相同,补充了一些自己的想法或这片题解可能没有注意到的细节。
看题目数据范围:\(1 \leqslant r,c \leqslant 10^6,1 \leqslant k \leqslant 10^{12}\),显然打暴力 \(\mathcal{O}(rc)\) 的时间复杂度是行不通的。必须做到近似于 \(\mathcal{O}(r)\) 的时间复杂度。
观察题目:题目中说:当 \(x+y=x \oplus y\) 时,这个格子是灰色的。而最后所求的答案就是走过的灰色的格子数,很容易想到斜着划分所有的格子,每一组的格子中的任意一个格子 \((x,y)\) 都满足 \(x+y=S\),其中 \(S\) 是不变的。如下图:(图可能有点丑,仅做示意)

接下来,我们针对某个特定的 \(S\) 进行考虑。设有一组 \((x,y)\),那么 \(x \oplus y=S\) 必然满足:\(S\) 二进制上的第 \(x\) 位为 \(1\),则 \(x\) 与 \(y\) 的二进制第 \(x\) 位上必然不同;而当 \(S\) 二进制上的第 \(x\) 位为 \(0\),那么 \(x\) 与 \(y\) 二进制第 \(x\) 位上必然相同。
再来考虑加法。首先看 \(S\) 二进制位的最后一个 \(1\),发现它有两种情况,通过后两位进位,或是由 \(x,y\) 中一个 \(0\) 一个 \(1\) 相加而成。
当它是通过后两位进位而成时,则 \(x,y\) 该位上相同则无法满足异或;不同,则无法满足相加(因为有进位)。(见下图 1)
而它是由更前面的某一位 \(0\) 对应的 \(x,y\) 中的 \(1\),也无法满足要求。(见下图 2)
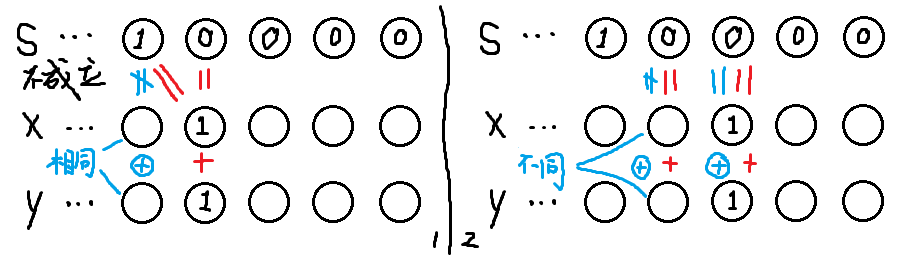
对于一个 \(S\),我们可以把它分为若干如上形式的二进制段,也可得出相通的结论。综上,在 \(S\) 的每一位 \(0\) 上,\(x\) 与 \(y\) 同为 \(0\) ;否则,\(x,y\) 有且仅有一个 \(1\)。
从这一点入手,统计某一斜行(由于斜行上各自数量可能不确定,我们这里用两个数确定一斜行 \((x,y)\) 表示从 \((0,y)\) 走到 \((x,y-x)\))上有多少个灰色格子(即 \(S=y\)),我们可以知道有一个 \(x^\prime \leqslant x\),其中 \(x^\prime\) 二进制上的每一位 \(1\),都对应了 \(x\) 与 \(y\) 上公共的 \(1\)。在这个 \(x^\prime\) 中,(对于一对二元组 \((p,q)\),这一步相当于枚举 \(x\) 的二进制位)我们可以知道 \(p\) 可以在这一位上取 \(1\)(\(q\) 取 \(0\)),或者取 \(0\)(\(q\) 相反)。而对于 \(y\) 某二进制位上为 \(1\),而 \(x\) 该二进制位上不为 \(1\),那么只可能 \(q\) 上取 \(1\),而 \(p\) 上为 \(0\)。
简单地说,就是将 \(y\) 分解成若干段形如 \(\texttt{1000...}\) 的二进制段,然后判断这些“段”与 \(x\) 是否对应。如果其最高位 \(1\) 与 \(x\) 对应,那么说明这一位可以 \(1\),答案加上后面的几段(注意!这里并不要求与 \(x\) 对应!)分别取 \(0\) 或 \(1\) 的总方案数。当然,这样算会少算一种情况,即所有对应二进制段上都取了 \(0\)。
理解了这个规律,我们可以写出这样一个用来统计某一斜行上灰色格子数量的函数:
ll type[64];
ll counting(ll x,ll y) {
ll res=1LL,cnt=0;
for(;y;res<<=1,y>>=1)
if(y&1) type[++cnt]=res;
res=0;
for(ll i=cnt;i>0;--i)
if(x-type[i]>=0) x-=type[i],res|=(1<<i-1);
return res+1;
}
解释说明:\(\operatorname{type}_i\) 表示 \(y\) 从高到低第 \(i\) 个 \(1\) 的权值。由于下标就相当于第几段,然后直接一边分解 \(x\) 一边计算答案就行了。1<<i-1 表示第 \(i\) 段后面有 \(i-1\) 段,每段取或不取的总方案数为 \(2^{i-1}\),由于每个二进制位都不会重复,可以直接用 |= 运算。
最后回到问题,统计走 \(k\) 步走过的灰色格子数,可以先统计从如下图红色部分的斜行的灰色格子数,然后统计如下图绿色部分的灰色格子数,累加走过的格子。当走不完某一斜行时,暴力模拟一下就可以了。这里细节有点多,就不赘述了。

(其中灰色部分可以帮助统计绿色部分)
完整代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll type[64];
ll counting(ll x,ll y) {
ll res=1LL,cnt=0;
for(;y;res<<=1,y>>=1)
if(y&1) type[++cnt]=res;
res=0;
for(ll i=cnt;i>0;--i)
if(x-type[i]>=0) x-=type[i],res|=(1<<i-1);
return res+1;
}
ll n,m,k;
int main() {
scanf("%lld%lld%lld",&n,&m,&k);
int drct=1;
if(m<n) swap(m,n),drct=0;
ll ans=0,done=0;
for(ll i=0;i<m;++i,drct^=1) {
ll cnt=min(i+1,n);
if(done+cnt<k) done+=cnt,ans+=counting(min(i,n-1),i);
else {
if(drct) for(ll p=min(i,n-1),q=i-min(i,n-1);done<k;--p,++q,++done)
ans+=p+q==(p^q);
else for(ll p=0,q=i;done<k;++p,--q,++done)
ans+=p+q==(p^q);
break;
}
}
if(done==k) {
printf("%lld\n",ans);
return 0;
}
for(int i=1;i<n;++i,drct^=1) {
ll cnt=n-i;
if(done+cnt<k) done+=cnt,ans+=counting(n-1,m+i-1)-counting(i-1,m+i-1);
else {
if(drct) for(ll p=n-1,q=m-n+i;done<k;--p,++q,++done)
ans+=p+q==(p^q);
else for(ll p=i,q=m-1;done<k;++p,--q,++done)
ans+=p+q==(p^q);
break;
}
}
printf("%lld\n",ans);
return 0;
}
完。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号