SD 一轮省集
Day 1
模拟赛 T1
给你 \(n,m,r,c,mod\)。定义一个 \(n\times m\) 的 \(01\) 矩阵是合法的,当且仅当其每个大小为 \(r\times c\) 的子矩阵中 \(1\) 的个数相等。求合法矩阵的个数。
\(n,m\leq 10^9,r,c,\leq 4\)。
首先可以注意到只要确定了最上面的 \(r\) 行以及最左边的 \(c\) 列,那么剩下的就可以递推出来。
但是确定了这些之后后面递推途中可能不合法,因为可能填着填着填不下了。尝试写出通项以更加详细地研究这个问题。
递推式是 \(a_{x,y}=a_{x,y-c}+a_{x-r,y}-a_{x-r,y-c}\),往后一直代入可以得到 \(a_{x,y}=a_{x,y\bmod c}+a_{x\bmod r,y}-a_{x\bmod r,y\bmod c}\)。
因为 \(a_{x,y}\in\{0,1\}\),所以当右式为 \(1+1-0\) 或 \(0+0-1\) 时不合法。注意到 \(a_{x\bmod r,y\bmod c}\) 与另外两项都不同,那么就是说想要合法另外两项的必须有至少一个与它相等。根据通项进一步可发现,对于 \(x\leq r,y\leq c\),考察 \(x\) 这一行所有模 \(c\) 同余 \(y\) 的位置,若其中有至少一个与 \(a_{x,y}\) 不等,则 \(y\) 这一列所有模 \(r\) 同余 \(x\) 的位置都与 \(a_{x,y}\) 相等。
然后可以使用你喜欢的方法随便做。
模拟赛 T2
\(m\times m\) 的平面上有 \(n\) 个点 \((x_i,y_i)\),点权是 \(a_i\)。定义一个三元组 \((i,j,k)\) 是合法的当且仅当 \(i<j<k\) 且两两点的曼哈顿距离中位数合法。定义一个中位数 \(x\) 合法当且仅当其是质数且满足 \(x\bmod 20=3\space\or\space x\leq 10\)。三元组 \((i,j,k)\) 的权值定义为 \(a_i+a_j+a_k\)。求所有合法三元组的权值和。
\(T\leq 5,n\leq 8000,m\leq 30000\)。保证平面中点坐标均匀随机。
看到这个奇怪几把限制打个表看看,发现范围内只有 \(700\) 个满足的,那么考虑枚举点对并钦定其距离为中位数。跑了一下大样例发现合法点对在 \(3\times 10^5\) 左右,看起来很可做,嗯。
对于每个点对,考察合法的另外一个点的位置,不难发现是分别以两个点为中心的菱形的异或。先转坐标系变成矩形,然后每个点对用三次二维数点容斥一下就做完了对吧。
对个吊。在边界会有算重的情况。要写狗屎分讨。据说还有一个 \(\log\) 分块的做法,好像也是狗屎。
模拟赛 T3
定义一个无向图 \(G\) 的线图 \(L(G)\) 为:在 \(L(G)\) 上用点代表 \(G\) 的每一条边,若 \(G\) 上两条边有公共端点则连接 \(L(G)\) 对应的两点(其实就是 NOIP T3 的那个玩意)。
给定图 \(G\),问其 \(k\) 阶线图复合后的最大独立集大小 \(\bmod 998244353\)。
\(n,m\leq 2000,2\leq k\leq 7\)。
首先经过观察可以得到,\(L(G)\) 的最大独立集大小相当于 \(G\) 的最大匹配大小,这也解释了为什么没有 \(k=1\) 因为这是无向图最大匹配只能 \(O(n^3)\) 做。
考虑 \(k=2\),也就是求 \(L(G)\) 的最大匹配。一个图的线图相对于普通图有什么性质?它是若干个团拼在一起。提溜出 \(L(G)\) 的一棵生成树,发现总是可以构造出大小为 \(\lfloor\frac{n}{2}\rfloor\) 的匹配。所以对于 \(G\) 中一个边数为 \(m\) 的连通块,\(L(G)\) 的最大匹配为 \(\lfloor\frac{m}{2}\rfloor\)。
考虑 \(k=3\),也就是求 \(L(L(G))\) 的最大匹配。根据 \(k=2\),只要求出 \(L(G)\) 每个连通块的边数就能知道答案。那么对于 \(G\) 的一个连通块,其 \(L(G)\) 的边数可以简单得到:\(\sum \binom{deg_i}{2}\)。
考虑 \(k=4\),同样的分析方法可以得到对于 \(G\) 中一个连通块,其在 \(2\) 阶线图中的边数为 \(\sum_{(u,v)\in E} \binom{deg_u-1+deg_v-1}{2}\)。
考虑 \(k=5\),继续分析就吃屎了。于是我们考虑什么样的一个子图才能在 \(3\) 阶线图中贡献一条边。画画所有情况再容斥一下。
考虑 \(k=6\),同 \(k=5\) 考虑所有情况。懒得想了,吃屎。
考虑 \(k=7\)。对 \(G\) 求出 \(1\) 阶线图然后带进 \(k=6\) 即可。时间复杂度 \(O(n^2+m^2)\)。
P6109
好这是一个静态 4-side 问题。考虑如果询问是 3-side,那么我们扫描线维护历史最值即可。那怎么转换呢?套个猫树分治就行了。
Day 2
模拟赛 T1
有一张 \(n\) 个点的无向完全图,其中每条边出现的概率都为 \(p\)。有一个操作:设点 \(u\) 距离为 \(1\) 的邻域的点集为 \(S_u\),选定满足 \(|S_u\cap S_1|\geq k\) 的 \(u\),连接 \((1,u)\)。问初始图经过操作能使 \(S_1=n\) 的概率为多少?对 \(998244353\) 取模。
\(n,k\leq 10^4\)。
若 \(k=1\),那么就是求初始图连通的概率。仿照连通图计数,设 \(f_i\) 为 \(i\) 个点连通的概率,枚举 \(1\) 所在的连通块大小,那么有:
移项得到 \(f_i\) 的递推式,可以 \(O(n^2)\) 计算。
若 \(k\) 没有限制,那么也考虑同样的方法。设 \(f_i\) 为 \(|S_1|=i\) 的概率,则有:
设 \(g_j=\sum_{t=0}^{k-1}\binom{j-1}{t}p^t(1-p)^{j-t}\),则原式可以 \(O(n^2)\) 计算。
模拟赛 T2
平面上 \(n\) 个点,\(m\) 个查询。每个查询给出查询区域正方形的对角线,问这个正方形内部有没有点。
\(n,m\leq 2\times 10^5,x,y\leq 10^8\)。
正方形是斜的不好做,先把它化成一个小正方形加上四个直角三角形(类似赵爽弦图),小正方形可以直接用二维数点解决。
考虑直角三角形,注意到询问是判定性问题。对其中一条直角边扫描线,扫描的途中在线段树上维护区间凸壳,查询就是拿斜边的斜率去切一个前缀的凸壳得到截距再跟斜边比较。\(O(n\log^2 n)\)。
QOJ7767
要维护很小范围的链邻域怎么做呢。考虑链修改本质上是把点重标号使得链上点编号连续,那么对于此题我们把一条重链的邻域也标号就好了,修改查询的时候对链顶特殊处理。可以做到 \(O(qk\log^2 n)\)。
P7215
如果想要一个城市当作首都,那么其两两之间的路径上的城镇所属的城市必须都被合并,但是这样会带来新的没连通的城镇,怎么做呢?
考虑点分治,对于一个分治中心求出令其成为首都的最小合并次数。但是有可能路径上的城市甚至这个分治中心就有城镇不属于这个分治区域,怎么办呢?
实际上如果有这样的城市,那么以当前分治中心作为城市一定不会更优。因为一直合并之后,上一个分治中心一定会被合并。
P4183
设 \(f_u\) 为点 \(u\) 到最近的叶子节点的距离,\(x\) 为贝西所在节点。称一个节点被控制当且仅当存在一个叶子节点能比贝西更快到这个节点,也即 \(f_u\leq \operatorname{dis}(x,u)\)。答案即为被控制的连通块个数。
考虑一个连通块一定是一个子树,设 \(d_i\) 为 \(i\) 的度数,则有 \(\sum d_i=2siz-1\),得到 \(1=\sum (2-d_i)\)。于是变成了点对统计问题,直接点分治即可。
Day 3
模拟赛 T1
有一个 \(n\) 个节点的森林,每个节点有一个关卡,属性有 \(c_i,p_i\),代表你打这个关卡需要 \(c_i\) 时间并且通关概率为 \(p_i\)。你能打这个关卡当且仅当其父亲已经被打通关或者其为根节点。如果打这个关卡失败了所有的关卡都要从头开始打。问通关时间的期望最小是多少。
\(n\leq 10^5,c\leq 10^6\),\(p_i\) 末尾保留六位小数。为了保留精度你只需要输出最小期望乘上 \(\prod p_i\) 的值就可以。
考虑如果所有点自成一棵树怎么做。期望题不取模事出反常必有妖,考虑贪心邻项交换,可以得到:
设 \(x_u=\frac{p_u-1}{c_u}\) 排序直接做就行。
因为是一棵树,还得考虑父亲儿子的偏序关系,但是这个很难考虑因为把这个强加进去就没有了偏序关系优美的传递性。考虑全局最小的 \(x_u\),可以知道如果他的父亲被选了那么他一定马上被选,所以就可以合并他们两个为一个连通块。而合并为一个连通块之后这个连通块的 \(x_u\) 也容易计算,所以用堆维护即可。
注意不能先全部做完了再乘上 \(\prod p_i\),要在合并两个连通块的时候就考虑。
模拟赛 T2
有一个 \(n\times n\) 的网格图,一开始全是空地,网格图外面一圈会有排着箱子,设 \(L_i\) 表示左侧边框从上往下第 \(i\) 个节点外面有多少箱子,\(R_i,U_i,D_i\) 同理。有一个操作,选定一个边框的一个位置,把它这一行或者列(取决你选的边框是左右边框还是上下边框)往里推一格。你要用这种操作将其推成指定的样子,判断是否可行并构造方案。
\(n\leq 500\)。保证 \(\sum (L_i+R_i+U_i+D_i)=\) 最终网格中箱子的个数。
推箱子的这个过程可以看作,找到这一 行/列 上第一个空地并把他变成箱子。
考虑最终一个箱子是从哪推过来的。发现如果其 上/下/左/右 有连续的 一列/一排 箱子跟边框连着,那么他就可能从那个方向推过来。把网格图上 \(n\times n\) 个点看成左部点,\(4n\) 个边框外面的箱子来源看成右部点,做带权二分图匹配。如果没有完美匹配就无解。\(O(n^3)\)。
现在考虑构造方案,一个箱子来源方向的所有箱子必须比他先放上。这可能不是 DAG。对于环我们考虑重新给每个点定向消除这些环,如图:
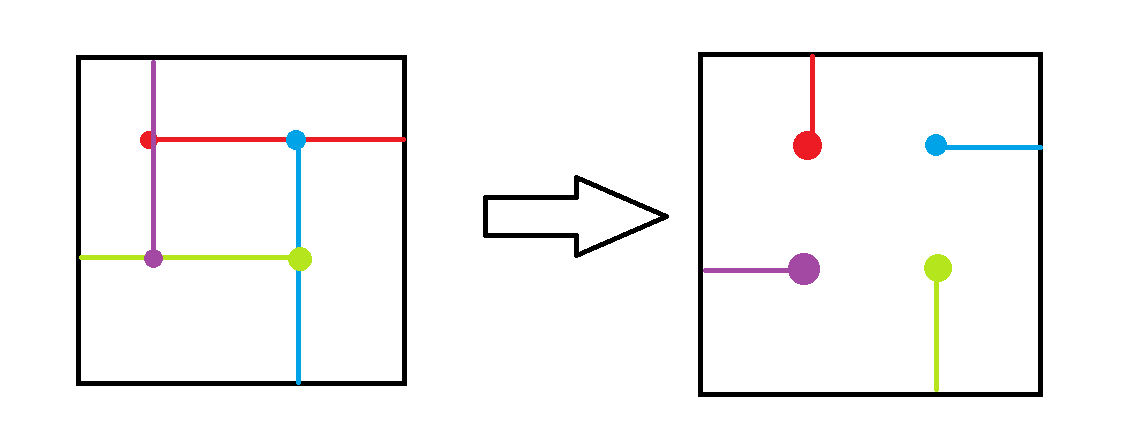
这么做的复杂度是多少呢?考虑势能分析。设势能为所有点到其匹配的边框的距离之和,初始势能为 \(O(n^3)\),每次消环势能必定减少,所以消环复杂度 \(O(n^3)\)。
模拟赛 T3
???
P5576
不会广义 SAM,口胡了一个东西。
考虑把所有串拼起来跑 SA,再给 \(sa\) 数组里每个串标上颜色表示其属于哪个字符串。查询就相当于问所有包含颜色 \([l,r]\) 的段里 \(\min h_i\) 的最大值。
考虑从大到小枚举答案 \(k\) 过程中合并 \(\min h_i\geq k\) 的连续段。对每个连续段里颜色排序,合并使用启发式合并,求出新增了哪些极大的颜色连续区间,那么所有的极大颜色连续区间数量是 \(O(n\log n)\) 级别的。
考虑这个极大的颜色连续区间对答案的影响,也就是 4-side 矩形 chkmax,单点查。扫描线直接做就是 \(O(n\log^3 n)\)。
但是这还不够。注意到矩形之间只有包含相离关系,那么扫描线之后就是区间插入,区间撤销,单点查。\(O(n\log^2 n)\)。
QOJ5034
这其实是一道字符串题。考虑每条路径相当于一个串,那么把这些串以及所有单点建出来一个 AC 自动机,在上面跑 Dijkstra。
但是有一个问题,转移边是 \(O(n^2)\) 级别的,不管是空间还是时间都难以接受。空间上,可以考虑用可持久化线段树来做。时间上,考虑有很多转移边实际上是无用的,点 \(u\) 相对点 \(fail_u\) 不同的出边只有 \(u\) 到儿子的那些,根据 Dijkstra 的贪心性质,这些相同的出边只需要被转移一次。转移的时候 dfs 当前版本整棵树,每转移一条边就将其对应节点在可持久化线段树上删去即可。\(O((n+m)\log n)\)。
Day 4
模拟赛 T1
一个 \(n\times n\) 的网格图,有 \(m\) 种颜色,每个点恰好有 \(m-n\) 种颜色不能涂。构造一个染色方案满足每行每列之中的颜色互不相同。
\(n\leq 500,m-n\leq 100\)。
不妨猜有解,我不会证明,课上的证明也忘了,课件里没写。
考虑枚举每个颜色填进网格里,那么这就是一个二分图匹配的过程。可以最大匹配直接做但是时间不对。
可以用稳定匹配搞一下但是我还没看懂,。
模拟赛 T2
强制在线区间异或区间 kth。
\(n,q\leq 10^5,V<2^{64}\)。
TL 9s,ML 512MB。
考虑怎么给 Trie 设计一个 tag 支持全局异或一个数,发现是好设计的,仿照机械生命体即可。
然后现在就有了一个 \(O(n\log n\log V)\) 时空的做法但是空间会爆,狗屎。
所以你需要写分块。对每个块建 Trie。修改散块重构,查询散块统一插进一个 Trie 里跟整块一块往下走,可以做到时间 \(O(n\sqrt n\log V)\) 空间 \(O(n\log V)\)。但是过不去。当然你可以直接写压位 Trie 但是我不会写。
考虑把 \(\log\) 放进根号下面。也就是说我们整块和散块要选一个做到线性。整块显然是不好做的,因为 \(O(1)\) kth 还是太困难了。考虑做散块。散块修改使用懒惰重构可以做到线性,现在我们只需要实现线性散块查询,也就是线性建 Trie。考虑建出 Trie 的虚树,叶子节点的 dfn 序排序就是这些数的顺序,那么我们现在只需要解决排序问题。
那么整数排序问题,怎么解决呢???考虑一开始排一次序,每次修改把被修改的那部分拉出来,此时这部分是有序的,可以线性建出虚树,然后给这棵树打上 tag 再 dfs 出来结果序列跟没修改的部分做归并即可。
时间 \(O(n\sqrt{n\log V})\),空间 \(O(n\log V)\),可以通过。
GYM104197G
直接设 \(f_{s,x,y}\) 表示从 \(x\) 到 \(y\) 经过了点集 \(s\) 是否可行,复杂度 \(O(2^nn^3)\)。
设 \(f_{s,x}\) 表示经过点集 \(s\) 以 \(x\) 结尾是否可行,因为是哈密顿路径所以一定经过 \(x\),对 \(y\) 计算答案时枚举合并即可。复杂度 \(O(2^nn^2)\)。
把 \(x\) 压进 DP 的值里,同时预处理一些东西能做到 \(O(2^nn)\)。
2022 南京 F
给定 \(k\),问一个正方形能否被分割为恰好 \(k\) 个锐角三角形,可行构造方案。\(k\leq 50\)。
首先一个三角形通过连接三边的中点可以变成四个跟原三角形相似的三角形,所以若 \(k\) 可行,则 \(k+3\) 也可行。通过一些方法我们能说明 \(k<8\) 无解,所以只要手工构造 \(k=8,9,10\) 即可。
Day 5
模拟赛 T1
给定一棵 \(n\) 个点的树,你需要给每个点分配非负点权满足所有点点权和恰为 \(m\)。设一个点权分配方案的价值为,选出编号最小的点 \(u\) 满足砍掉 \(u\) 这个点以及其相连的所有边之后,所有连通块的点权和都不大于 \(\frac{m}{2}\)。求所有点权分配方案的价值和。
\(n\leq 3\times 10^5,m\leq 10^6\)。部分分 \(m\) 为奇数。
首先注意到如果有一个连通块的点权不满足条件,那么就只可能有这一个连通块不满足。但是还有点权最小的限制非常恶心,思考一下,对于一种点权分配方案,有哪些点能满足这个条件?发现这个限制类似树上重心,但是这个题点权可以是 \(0\),但是 \(m\) 为奇数的时候肯定只有一个点所以枚举哪个连通块不符合条件拿插板法统计一下即可。这个式子计算一次是 \(O(m)\) 的推一推式子可以做到 \(O(1)\) 查询。
再考虑偶数,经过一些手玩发现若 \(u,v\) 都是重心,那么 \(u\to v\) 路径上所有点都是重心,进一步可以发现所有重心恰好构成一条路径,这条路径上和路径两边挂着的子树权值都为 \(0\),两边的子树权值都为 \(\frac{m}{2}\)。于是考虑进一步容斥。如果现在要统计 \(u\) 的贡献次数,那么先不管最小值限制统计出来一个次数,再考虑一条路径为重心。可以找出点集 \(V\) 满足 \(v\in V,u\to v\) 路径上只有 \(v\) 满足 \(v<u\),然后减去 \(u,v\) 配对方案数,再加上 \(V\) 中两两配对方案数即可。
这个过程可以从大到小枚举点用并查集合并简单维护,但是我们现在来处理上面的式子。设 \(x\) 个点的子树点权和大于 \(\frac{m}{2}\) 带来的不合法的方案数为:
一种组合意义是,长为 \(n\) 的不降数列 \(a\),设 \(p=\lfloor\frac{m}{2}\rfloor+1\),需要保证 \(a_x\geq p\)。那么考虑构造一个序列 \(b\) 满足 \(b_i\) 为最小的 \(j\) 满足 \(a_j\geq i\),容易发现构成双射且 \(b\) 不降。现在限制转变为 \(b_p\leq x\),容易写出式子:
直接递推即可预处理。
模拟赛 T2
有一个长为 \(n\) 的数列 \(a\) 和一个参数 \(t\)。\(q\) 次操作 \((l,r)\):给区间 \([l,r]\) 做一次冒泡排序.若 \(t=1\) 则在所有操作结束之后输出结果序列,若 \(t=2\) 则在每次操作之后输出区间 \([l,r]\) 的和。
\(n\leq 10^6,q\leq 10^4\)。
考虑全局操作怎么做。冒泡排序一轮的实质,其实是对于一个前缀 \(\max\),让他往后跳到下一个前缀 \(\max\) 所在的位置。设 \(f_i\) 为 \(a_i\) 前面比 \(a_i\) 大的数的个数,则前缀 \(\max\) 就是 \(a_i=0\)。做一轮冒泡排序会让所有大于 \(0\) 的 \(p_i\) 统一减去 \(1\)。所以对于全局操作 \(t=1\),求出初始序列的 \(p_i\),冒泡排序途中前缀最大值的值一定不降,用堆维护即可。\(t=2\) 是送的。
考虑区间操作。尝试操作分块。每 \(B\) 次操作重构一次,对于这 \(B\) 次操作,把所有的左右端点找出来划分成块,这样每次操作是若干整块而且块数在 \(O(B)\) 级别。对于每个块维护其 \(f_i\),考虑一次操作相邻的两个块,他们之间可能会发生交换。对于左边的块来说是一个单点修改,直接改即可;对于右边的块,其可能会让一些 \(f_i\) 增大,但是紧接着会把换上来的这个数冒泡换过去,相当于 \(f_i\) 没变。
感觉不是很清晰,以后再补,
模拟赛 T3
给你 \(n\) 个串,求三元组 \((i,j,k)\) 的个数:\(i,j,k\) 不相同,\(S_i\) 是 \(S_j\) 的子串,\(S_j\) 是 \(S_k\) 的子串,且不存在另外一个 \(j'\) 满足前面这些条件。
还没懂。
QOJ4812
首先有一个暴力,设 \(f_{s,i}\) 为和为 \(s\),末尾为 \(i\) 的贡献之和,直接 DP。
注意总和是 \(n\),而每次变化的量很小,联想到公差为 \(1\) 的等差数列和是平方级别的,启示我们考虑阈值分治。
设一个阈值 \(B\)。若 \(a_1<B\) 则跑暴力,第二维显然是 \(O(B)\) 级别的,复杂度 \(O(nB)\)。
否则,数列长度一定为 \(O(\frac{n}{B})\) 级别的,但是此时不能把 \(a_1\) 记到状态里,考虑设 \(g_{i,j,s}\) 为数列第 \(i\) 位,\(a_i-a_1=j\),\(\sum_{j=1}^i(a_j-a_1)=s\) 的贡献,复杂度是 \(O(\frac{n^3}{B^2})\),直接平衡得到 \(O(n^{5/3})\)。
考虑在数列最前面加上一个数产生的影响。重设 \(g_{i,s}\) 表示长为 \(i\),\(\sum_{j=1}^i(a_j-a_1)=s\) 的贡献,转移相当于把后面这一坨拼到当前 \(a_1\) 上然而我们并不关心 \(a_1\) 是多少,而且这样避免了记录 \(a_1\)。这个 DP 复杂度是 \(O(\frac{n^2}{B})\) 的,直接平衡得到 \(O(n^{3/2})\),可以通过。
QOJ7677
考虑直径怎么刻画,答案是记录直径的中点,因为所有的直径拥有共同的中点。分类讨论一下中点是在边上还是在点上。
如果在边上,那么当且仅当把一边的直径端点删完之后,中点才会向另外一边移动 \(\frac{1}{2}\) 的距离。在点上的话,需要把除了一个子树之外的直径端点全部删完。
注意到只有中点移动方向的直径端点才有可能没被删干净,所以把树上一条边拆成两个单向边,设 \(f_{i,j,k}\) 表示中点上次沿着 \(i\) 移动,直径长度为 \(j\),中点上次移动指向的子树被删了 \(k\) 个直径端点。状态数显然 \(O(n^2)\)。
如果 \(j\) 为奇数,说明中点在边上,讨论一下是哪边先删完,相当于是有 \(x\) 个白点 \(y\) 个黑点,每次可以选一个点删掉,问白/黑点先被删掉且另一边留下 \(z\) 个点所有情况的方案数,这个用另外一个 DP 计算出转移。
如果 \(j\) 为偶数,说明中点在点上。枚举一下转移到那棵子树跟上面同样处理即可。
Day 6
模拟赛 T2
在平面直角坐标系上,有两条横坐标分别为 \(0\) 和 \(w\) 的无限长竖直线段。现在有 \(n\) 只蚂蚁要按照编号从小到大的顺序依次行动,每只蚂蚁形如 \((a,b,c)\),表示从 \((0,a)\) 走到 \((w,b)\),中途若碰到线段就停下来,且若 \(c=1\),就在其行动轨迹上留下一条线段。对于每只蚂蚁求出其终点坐标,用分数表示。
\(n\leq 3\times 10^5,a,b\leq 10^9,c\in\{0,1\}\)。部分分:\(a_i\) 单增。
考虑部分分,不妨维护一个最靠上的分界线,若新加入的直线碰到这条分界线就停止。容易发现这个分界线是一个下凸壳,直接维护即可。
如果不单增,那么把所有 \(a_j>a_i\) 的线段拉出来组成一个上凸壳,\(a_j<a_i\) 的线段拉出来组成一个下凸壳,合成一个凸包然后判断交在哪就行。弱智。\(O(n\log^2n)\)。
但是还有另外一个东西。注意到如果把线段交点看成图中节点,连接两点的线段看成图中边,则这个图是一个森林。于是加线段相当于加叶子,要查询凸包只需要查询上下第一个点的树上路径即可。\(O(n\log n)\)。
Day 7
模拟赛 T1
有两个长为 \(n\) 的序列 \(a,b\),你只知道序列 \(b\)。你每次可以花费 \(\gcd_{i=l}^rb_i\) 的代价知道 \(\sum_{i=l}^r\) 的值,问至少需要多少代价才能知道每一个 \(a_i\) 的值?带修,每次单点修改 \(b_i\)。
\(n,q\leq10^5,b_i\leq10^9\)。
先对 \(a\) 做一个前缀和 \(s\),那么问题变为花费代价查询 \(s_r-s_{l-1}\) 的值,需要知道 \(s\) 的所有值,其中 \(s_0\) 已知为 \(0\)。
调整法发现一定会查一次 \([1,n]\)。这样就有了两个已知的值,\(s_0\) 和 \(s_n\)。现在需要围绕已知的这两个值推出来整个 \(s\),不难想到建一个图,若查询区间 \([l,r]\),则在图上连边 \((l-1,r)\)。那么问题转化为要在这样一张图中求出最小生成树。
考虑到 \(\gcd\) 有区间包含单调性,猜想一个点一定要么只与 \(0\) 有连边,要么只与 \(n\) 有连边。证明也是调整。如果跟 \(0,n\) 都没有连边(以下以 \(0\) 为例),那么找出 \(i\to 0\) 的路径,发现 \((0,i)\) 这条边一定不是权值最大的。那么现在问题转化为求出 \(\sum_{i=1}^n\min\{\gcd_{j=1}^ib_j,\gcd_{j=i+1}^nb_j\}\)。
发现是前缀 \(\gcd\) 和后缀 \(\gcd\) 的形式,上次遇到这个 trick 被击杀了,这一次我将拿回属于我的一切!直接线段树上二分求出 \(\gcd\) 变化的位置,然后瞎统计就行。\(O(n\log^2n)\)。
模拟赛 T2
给定 \(n,k\),求出所有长为 \(n\) 字符集大小为 \(k\) 的字符串中本质不同的回文子串个数和。
\(n\leq 128,k\leq 10^5\)。
注意到一个回文子串的贡献信息只与其 border 集合有关,所以问题化为三个子问题:
- 枚举所有 border 集合 \(T\):用并查集维护,uint128 压缩状态。
- 计算有多少个串 t 的 border 集合是这个集合:直接求出并查集连通块个数,但是需要容斥。若 \(T\subset S\),则 \(f_T\) 需要减去 \(f_S\)。
- 计算有多少个串 \(s\) 包含了 \(t\) 至少一次:设 \(f_i\) 为 \(t\) 出现在 \(s\) 的 \(i-|t|+1\sim i\) 中且这是 \(t\) 第一次出现的方案数,则容斥减去之前的就可以。
\(O(能过)\)。
Day 8
模拟赛 T1
给你一个 \(n\) 个点 \(m\) 条边的无向图。每条边权值有规定范围 \([l_i,r_i]\),需要给每条边分配权值满足每条边的权值在范围之内,所有边权构成 \(1\sim m\) 的排列,且整张无向图的最小生成树是由编号前 \(n-1\) 条边组成的。可行输出解无解输出无解。
\(m\leq5\times 10^5\)。
考虑 \(m=n-1\),直接按左端点排序从小到大维护一个堆每次把右端点最小的拿出来贪心就行。
如果有非树边,考虑树边与非树边的相互影响。显然非树边的 \(l\) 应该是树上这条路径的 \(l\) 的 \(\max+1\),树上路径的 \(r\) 要对非树边的 \(r-1\) 取 \(\min\)。然后对着这个跑 \(m=n-1\) 构造可行解就行。
直接树剖 \(O(n\log^2n)\),离线树上差分可以做到 \(O(n\log n)\)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号