斜率优化 dp · 学习笔记

动态规划模型

\[f_i=\min_{L(i)\leq j\leq R(i)}\{f_j+val(i,j)\} \]

形如这种的线性动态规划叫做 1D/1D 动态规划。

众所周知，当 \(val(i,j)\) 不包含和 \(i,j\) 同时相关的项时，我们可以使用单调队列来优化到均摊 \(O(1)\) 决策。

然而，当 \(val(i,j)\) 包含 \(i,j\) 乘积项时，使用单调队列并不能很好地解决这类问题，于是就引入了斜率优化。

例 AT_dp_z

设走到 \(i\) 的最小花费是 \(f_i\)，则有：

\[f_i=\min_{1\leq j< i}\{f_j+(h_i-h_j)^2+C\} \]

朴素 DP，\(O(n^2)\)，显然无法通过。

暴力拆开，得：

\[f_i=\min_{1\leq j< i}\{f_j+h_i^2-2h_ih_j+h_j^2+C\} \]

把与 \(j\) 无关的常量项提出，有：

\[f_i=\min_{1\leq j< i}\{f_j-2h_ih_j+h_j^2\}+h_i^2+C \]

Step 1 · 判断决策

假设 \(1\leq j_1<j_2\leq n\)，且 \(j_1\) 比 \(j_2\) 更优，则有：

\[f_{j_1}-2h_i h_{j_1}+h_{j_1}^2 \leq f_{j_2}-2h_i h_{j_2}+h_{j_2}^2 \]

参变分离，\(i\) 是参数：

\[2h_i(h_{j_2}-h_{j_1})\leq f_{j_2}+h_{j_2}^2-(f_{j_1}+h_{j_1}^2) \]

\[2h_i\leq \frac{f_{j_2}+h_{j_2}^2-(f_{j_1}+h_{j_1}^2)}{h_{j_2}-h_{j_1}} \]

设 \(Y(j)=f_j+h_j^2\)，\(X(j)=h_j\)，则有：

\[2h_i\leq \frac{Y(j_2)-Y(j_1)}{X(j_2)-X(j_1)} \]

Step 2 · 确定凸包

我们把一个决策 \(j\) 抽象成一个点 \(P(X(j),Y(j))\)。

设 \(\operatorname{slope}(i,j)=\frac{Y(i)-Y(j)}{X(i)-X(j)}\)，也就是 \(i,j\) 两点所连成直线的斜率。

假设有 \(i<j<k\) 三个点，当在给 \(f_p\) 做决策的时候，满足 \(j\) 最优，那么当且仅当 \(i\) 比 \(j\) 劣 且 \(j\) 比 \(k\) 优，用式子表示就是：

\[\operatorname{slope}(i,j)\leq 2h_p \]

\[\operatorname{slope}(j,k)\geq 2h_p \]

合并一下：

\[\operatorname{slope}(i,j)\leq\operatorname{slope}(j,k) \]

因此，如果有 \(i<j<k\) 不满足上式，则 \(j\) 一定不可能是最优决策，也就是说，当 \(i,j,k\) 形如下图时，\(j\) 可以被删除。

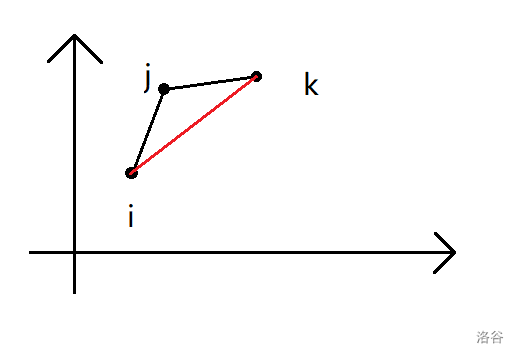
现在我们决策集合中，每一对相邻的 \(i,j\) 都满足上式，最后我们的决策集合长得就像下图一样，我们叫它：凸壳。

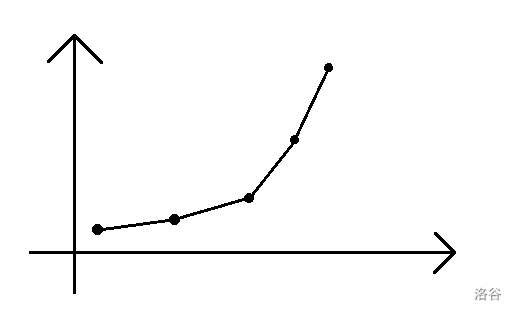
Step 3 · 维护凸包

我们要时刻保持决策集合满足这样的条件。假设，对于 \(1\leq j<i\)，\(P(j)\) 都已经被维护好了，现在要插入 \(P(i)\)。

因为本题中 \(X(j)\) 也就是 \(2h_i\) 是单调的，所以 \(P(i)\) 是在队尾插入的，所以我们可以使用一个单调队列，这个单调队列里相邻两个决策的斜率值单调递增。当我们插入 \(P(i)\) 时，若 \(P(i)\) 和队尾点构成的斜率值 大于 队尾点和队尾点前面的一个点时，把 \(P(i)\) 插入到队尾。否则一直弹出队尾点，直到满足上述条件。

Step 4 · 总结

看回我们最初的状态方程

\[f_i=\min_{1\leq j< i}\{f_j+(h_i-h_j)^2+C\} \]

我们只要找到最优的 \(j\)，就能完成转移。

还是看我们的基本公式：当 \(2h_i\leq\operatorname{slope}(i,j)\) 时，\(i\) 比 \(j\) 优。

因为凸包上斜率单调递增，所以我们可以使用二分来寻找一个最小的 \(k\)，使得 \(2h_i\leq\operatorname{slope}(k,k+1)\)。

至此，我们已经可以以 \(O(n\log n)\) 的复杂度通过此题，但是还有优化的空间。

发现算法的瓶颈在二分的过程，考虑使用单调性相关性质。

我们知道 \(2h_i\) 是单调的，所以每次找到的 \(k\) 也是单调的，换句话说，这一次找到了 \(k\)，那么以后就不可能找到比 \(k\) 还往前的点。

所以我们可以判断 \(2h_i\leq \operatorname{slope}(1,2)\)，如果符合，\(1\) 就是最佳决策点，否则一直弹出队头，直到满足。

此时均摊复杂度 \(O(n)\)。

* 李超线段树解法

看回我们的基本公式：

\[f_i=\min_{1\leq j< i}\{f_j-2h_ih_j+h_j^2\}+h_i^2+C \]

我们只需要让 \(\min\) 里面的东西最小就行了，令 \(k=-2h_j\)，\(b=f_j+h_j^2\)，再让 \(g(x)=h_ik+b\)，则：

\[f_i=\min_{1\leq j< i}\{g(j)\}+h_x^2+C \]

其中 \(g(x)\) 明显是一个一次函数，所以我们可以使用李超线段树来维护每个决策点，每次决策查询最小值即可，时间复杂度 \(O(n \log n)\)。