P11050 [IOI2024] 消息篡改者

作为一个人我们该如何想到正解？？？

本题解讲了很多部分分做法。若想直接看正解可直接翻到最下面查看。

10 pts

考虑如何发送准确无误的信息。

注意到有 \(16\) 个位不会被篡改，那么只要把这 \(16\) 个位全填上你想发送的数，那么不论 C 怎么修改剩下的 \(15\) 位，发送过去消息的众数一定是你想发送的数。

用这种策略发送 \(S\) 次即可获得 \(10\) 分的好成绩。

30 pts

考虑到如果我们知道哪些位不会被捣乱，那么我们只需要最多 \(64\) 次满载荷的发送即可发送全部消息。

还有一个问题需要解决，如果我们不能保证正好在最后一条消息的结尾发送完 \(M\)，那么我们不知道应该从哪结束。

解决方法是，把最后空的位设为 \(M\) 最后一位取反后的二进制位，这样我们接收完所有消息只需要删掉最后相同连续的一段即可。注意如果恰好发送完则需要再发一整段空的消息。

我们不妨用上面那种暴力策略发送 \(31\) 次，把 \(X\) 发送过去，然后使用 \(64\) 次满载和发送，即可获得 \(30\) 分的好成绩。

乱搞（50 pts）

考虑在发送 \(X\) 的过程中我们当前已知 \(a\) 位是永远不会被捣乱的，则我们可以一次发送 \(i\) 位而不是一位一位地用暴力策略发送。

这样在最坏情况下大约是 \(20+64\) 次通信，可以获得 \(45\) 分的好成绩。

考虑使用一次暴力发送来决定是从左边开始发送还是右边开始发送，那么最坏情况大约是 \(17+64\) 次通信，可以获得 \(51\) 分的好成绩。

83 pts

考虑到这样的关键一点：

若先找到一个永远不会被捣乱的位，那么就可以使用这一个位通信 \(31\) 次来发送 \(X\)，让剩下 \(15\) 个不会被捣乱的位先发送着 \(M\)。

因为我们可以把未了解 \(X\) 全貌时的消息存下来，等知道 \(X\) 全貌了之后再用以前的消息来获得先发送的 \(M\)。

那么如何找到一个 \(X_i=0\) 的位呢？

不妨钦定发送第一个 \(X_i=0\) 的位置。考虑到一共有 \(31\) 个位，其中有 \(16\) 个位为 \(0\)，所以第一个 \(0\) 的位置最大在 \(16\)（前 \(15\) 个都是 \(1\)），这 \(16\) 种情况我们可以映射到区间 \([0,15]\) 中，以此来实现 \(4\) 次暴力发送来找到第一个 \(0\) 的位置。

知道了第一个 \(0\) 的位置，那就只需要 \(29\) 次发送即可获得 \(X\)，因为已经知道的算一个，通过数量关系推出来的还可以算一个！！

总结一下，首先需要 \(4\) 次暴力发送来找到第一个 \(0\) 的位置，然后发送 \(29\) 次把整个 \(X\) 发送过去的同时，发送 \(15\times 29\) 个 \(M\) 中的位，最后再用 \(\lceil \frac{1024-15\times 29}{16}\rceil=37\) 次发送来发送剩下的所有消息。总共 \(70\) 次，可以获得 \(83\) 分的好成绩！！！

87 pts

注意到 \(66\) 次即可获得满分的好成绩，但是 \(66\) 次最多发送 \(1024+32\) 位的有用信息，这就说明最多使用两次暴力发送。

于是可以想到，把 \(31\) 个位划分成 \(4\) 个子区间，长度分别是 \(8,8,8,7\)，由鸽笼原理可知一定存在一个区间使得其 \(0\) 的个数要大于 \(1\) 的个数。

先用 \(2\) 次暴力发送来找到这个区间，然后用这个区间来发送这个区间第一个 \(0\) 的位置，剩下区间用来先发送着消息 \(M\)。

然后又知道这个区间第一个 \(0\) 的位置最大是 \(4\)，所以能用 \(2\) 次发送来获得这个区间里第一个 \(0\) 的位置！！！

梳理一下，我们先用 \(2\) 次暴力发送来找到一个区间使得其 \(0\) 的个数大于 \(1\) 的个数。然后用 \(2\) 次发送来找到这个区间里第一个 \(0\) 的位置，同时用剩下最少 \(11\) 个 \(0\) 发送 \(2\times 11\) 个 \(M\) 中的位。再然后用 \(29\) 次发送来发送 \(X\)，同时发送 \(29\times 15\) 个 \(M\) 中的位。最后用 \(\lceil \frac{1024-15\times 29-11\times 2}{16}\rceil=36\) 次发送来发送整个 \(M\)。

一共需要 \(69\) 次发送，可以获得 \(87\) 分的好成绩。

90 pts

上面的方法最重要的启发是，可以只用一个区间来使用众数暴力发送，其他的位先发送着 \(M\)。

然后又知道，把这 \(31\) 个位等分成几段，必定存在一段使得其中 \(0\) 的数量大于 \(1\) 的数量。

所以，可以采用如下策略：

• 把这 \(31\) 个位分成 \(16\) 个区间（如图所示，这是一个类线段树结构，让前 \(30\) 个每两个成一个区间，第 \(31\) 个自己成一个区间）。

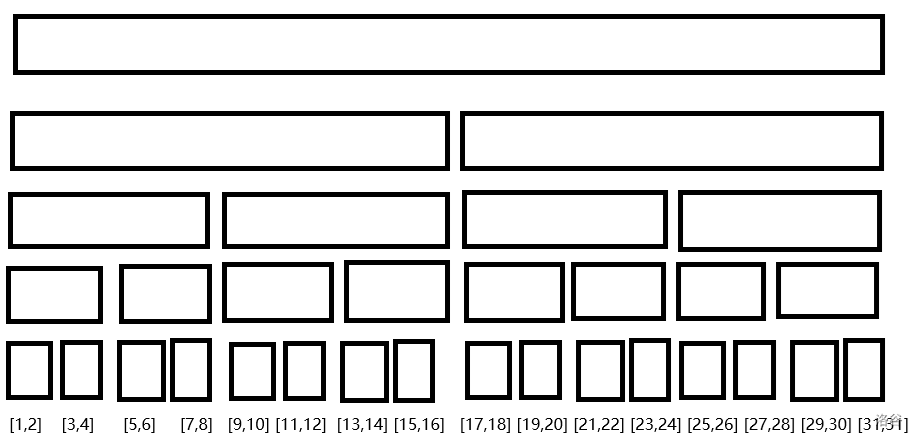
• 这其中必定有一个区间其 \(0\) 的个数大于 \(1\) 的个数。

• 于是使用 \(4\) 次发送，区间内的数的众数表示每次往左还是往右走来找到最底下这一层的区间，剩下的用来发送 \(M\)。

• 所以最多会浪费掉 \(16+9+5+3=33\) 个位，能获得 \(90\) 分的好成绩。

100 pts

震撼。跟上面的做法一点关系都没有。

界是 \(66\)，这个界太紧了。考虑怎么使用 \(31\) 位发送 \(X\)。

观察到一次消息有 \(31\) 个位，而有 \(16\) 个位是不会被篡改的。虽然之前挖掘了这个绝对众数的性质，但还是不够彻底。

之前的想法还是太局限了，考虑把每一列看成一个消息。设每个可用位到下一个可用位的循环距离为 \(d\)，则我们在这一位的前 \(d-1\) 次发送 \(0\)，第 \(d\) 次发送 \(1\)，之后照常传递数据。

这样，每一位都会有一个出边，画到图上就是一个内向基环树森林。根据可用位发送的出边一定构成一个大小为 \(16\) 的环，而剩下 \(15\) 个点再怎么乱连也不可能连出另外一个大小为 \(16\) 的环，所以只用了 \(31\) 位就发送了 \(X\)。

太厉害了。