PyTorch 深度学习实践 第6讲：逻辑斯蒂回归

逻辑斯蒂回归

视频教程

1.线性模型与逻辑斯蒂回归模型区别？

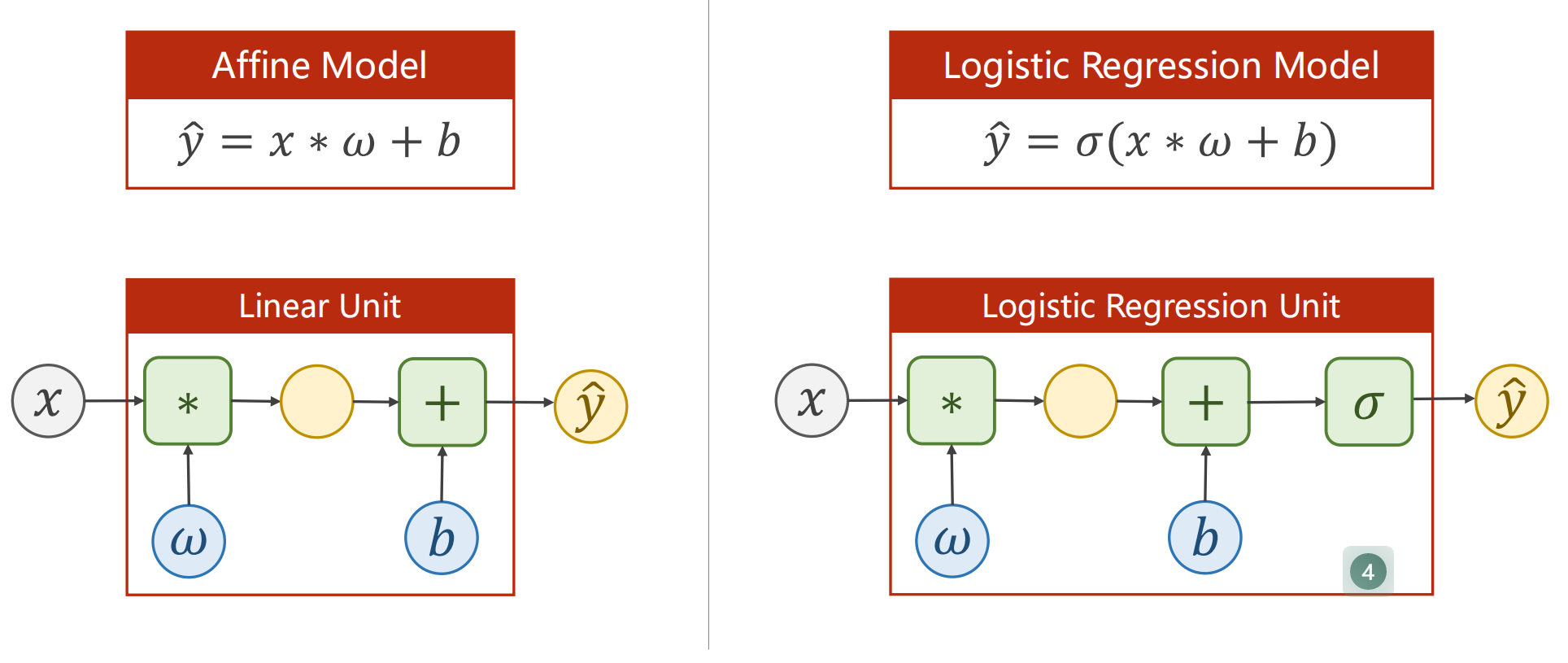
说明：

1. 多了sigmoid函数
2. 计算损失时有区别

2.为什么选用sigmoid函数？

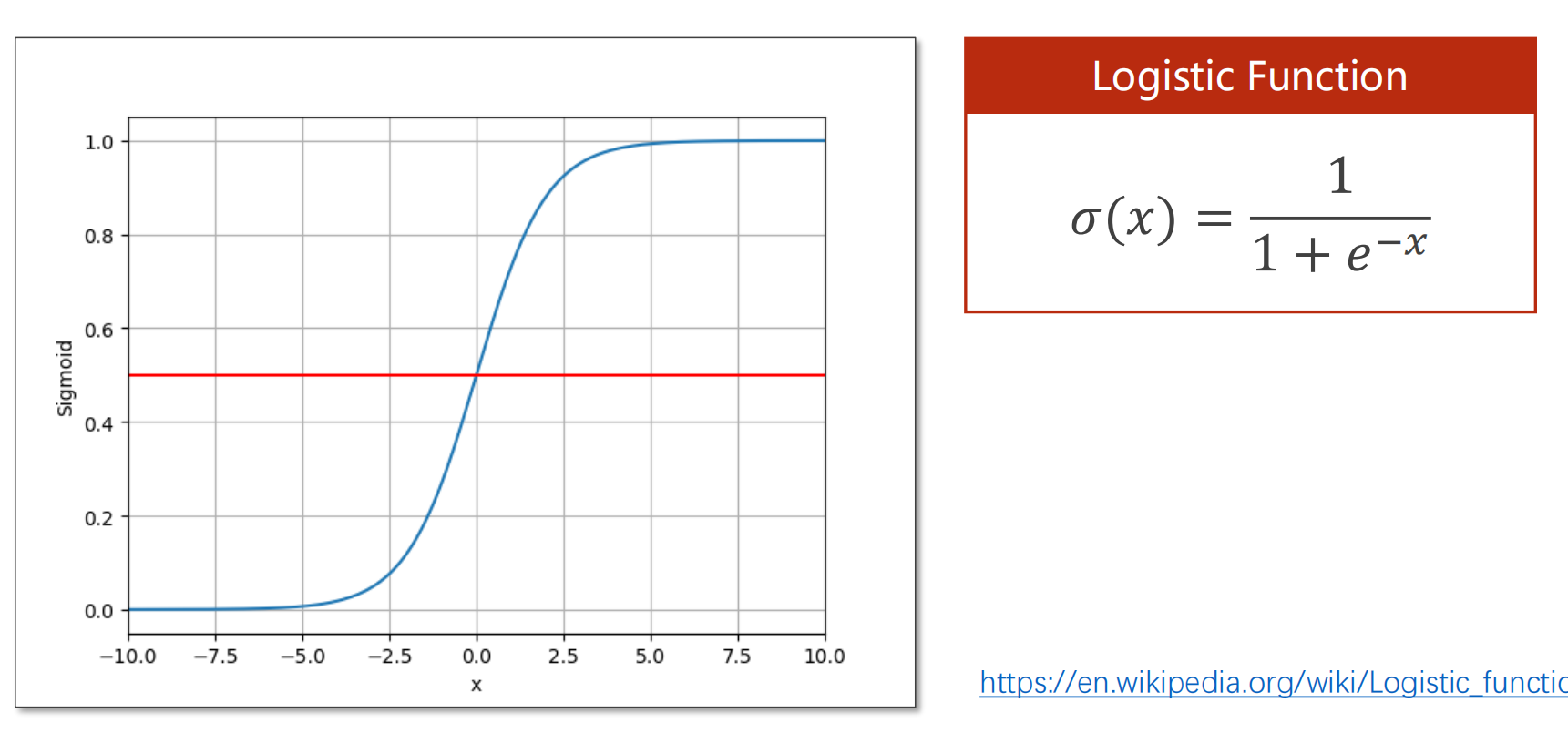
说明：

• 回归问题：输出是个R，分类问题：输出是某个分类的[0,1]的概率
• 利用sigmoid函数将R映射在概率取值范围[0,1]区间上

3.怎样计算二分类的损失函数?

说明：

1. 前者计算y_pred与y之间的差距
2. 后者用交叉熵cross-entropy计算分布之间的差异

4.二分类的小批量损失函数？

说明：
发现y与y^ 越接近，BCE损失越小

• 当y=1,要损失最小，需要y^最大（不会超过1），越接近于1即可
• 当y=0,要损失最小，需要y^最小（不会超过0），接近于0即可
• so~y与y^越接近，BCE损失越小
• minibatch 损失是多个样本的BCE损失求均值
  

import torch
import torch.nn.functional as F

#1.准备数据
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])

#2.设计模型
class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel,self).__init__()
        #此处类的实例化，需要定义初始参数，
	#这些参数会在你做forward和 backward之后根据loss进行更新,
	#所以通常存放在定义模型的 _init_() 中
        self.linear = torch.nn.Linear(1,1)
		
    def forward(self,x):
        y_pred = F.sigmoid(self.linear(x))#此处y^套入sigmoid函数代替变量x
        return y_pred
    
model = LogisticRegressionModel()

torch.nn.functional.x则需要把相应的weights 作为输入参数传递,才能完成运算, 所以用torch.nn.functional创建模型时需要创建并初始化相应参数.

#3.构造损失函数和优化器
criterion = torch.nn.BCELoss(size_average=False)#用交叉熵计算损失，内部参数询问是否求均值，均值会影响loss的求导，相当于乘以系数，所以，最终影响学习率的选择
optimizer = torch.optim.SGD(model.parameters(),lr = 0.01)

#4.循环训练
for epoch in range(1000):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch ,loss.item())
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

0 2.4510953426361084
1 2.4456307888031006
2 2.44039249420166
3 2.435363292694092
4 2.4305272102355957
5 2.425868272781372
6 2.4213733673095703
7 2.4170291423797607
8 2.4128246307373047
9 2.408748149871826
10 2.404790163040161
......
982 1.1300536394119263
983 1.1294807195663452
984 1.1289081573486328
985 1.1283364295959473
986 1.127765417098999
987 1.127195119857788
988 1.1266255378723145
989 1.1260567903518677
990 1.125488519668579
991 1.1249209642410278
992 1.1243541240692139
993 1.1237879991531372
994 1.1232225894927979
995 1.1226577758789062
996 1.122093677520752
997 1.1215301752090454
998 1.1209672689437866
999 1.1204053163528442
PyTorch 深度学习实践 第6讲

【pytorch】torch.nn 与 torch.nn.functional 的区别