BFS 846. 树的重心

每日一道算法日常预防老年痴呆。

 

先上题目

给定一颗树，树中包含n个结点（编号1~n）和n-1条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式
第一行包含整数n，表示树的结点数。

接下来n-1行，每行包含两个整数a和b，表示点a和点b之间存在一条边。

输出格式
输出一个整数m，表示重心的所有的子树中最大的子树的结点数目。

数据范围
1≤n≤105
输入样例
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例：
4

 

根据题目把示例图画了出来：

 

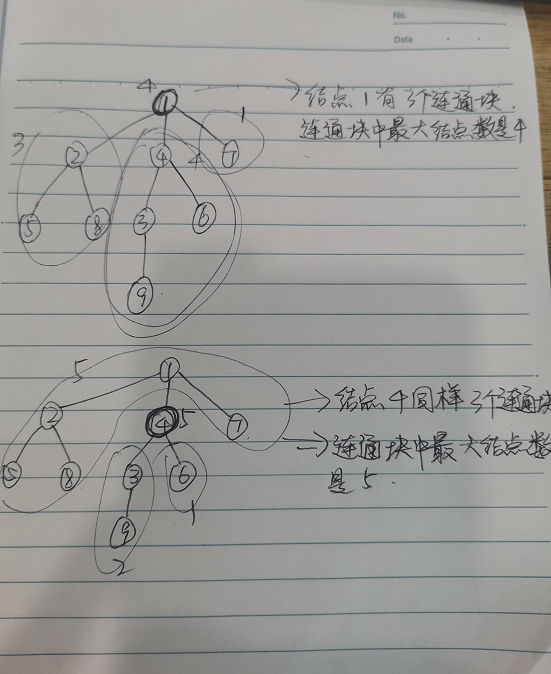
这里是拿点1和点4做树的重心来做示范，题目的要求是在连通块最多的节点数当中求出最小的数。

解题思路：模拟一个队列存储节点，入队头节点（假设这就是树的重心）以后，开始搜索该节点的所有连通块，然后返回所有连通块当中最大的节点数。最后求所有节点的最大节点数当中的最小数值。本题的难点在于，如果头结点不是根节点了，（比如说现在要搜索节点4的连通块了）我们要如何向上搜索与节点1相连的那个连通块有多少个节点数？

解决方法是其实可以直接把节点4看成一个根节点，与之相连的节点1所在的连通块的节点数，其实就是 所有的节点数 - 节点4这一连通块的总数。

详见代码注释

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 1e5+10;

int h[N], e[2*N], ne[2*N];  //因为是无向图 考虑有两条边 所以开N*2
int idx = 0;    
int n, ans = N;
bool st[N];     //判断当前节点有没有搜索过

void add(int a, int b)  //模拟一个队列
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

int dfs(int u)
{
    int size = 0;   //存储当前连通块节点数
    st[u] = true;   //头结点标记为已遍历
    int sum = 0;    //选中点的子树的节点数
    for(int i = h[u]; i != -1; i = ne[i])   //从给定的节点内开始深搜
    {
        int j = e[i];
        if(!st[j])      //如果深搜到一个没有走过的节点
        {
            int s = dfs(j);     //存储当前节点子树的所有节点数
            size = max(size, s);    //取子树节点数中的最大值
            sum += s;       //遍历完一个连通块 就把子树的节点数累加
        }
    }
    size = max(size, n - sum - 1);  //如果不是头结点，还需要比较子树节点和连接头结点的连通块哪个数值更大
                                    //n - sum - 1是去掉当前节点后，父节点所在连通块的大小
    
    ans = min(ans, size);   
    
    return sum + 1;     //返回sum+1是因为 sum是选中点的子树的节点数，这里需要把选中的点也算进去 所以+1
}


int main()
{
    memset(h, -1, sizeof h);
    scanf("%d", &n);
    
    for(int i = 0; i < n - 1; i++)
    {
        int a,b;
        scanf("%d%d", &a, &b);
        add(a, b);      //无向边所以要添加两次
        add(b, a);
    }
    
    dfs(1);
    cout<<ans<<endl;
    return 0;
}