国庆集训笔记

Day1

D1 Note

文件名必须满足与英文题目名字相同。
把文件放在对应文件夹里面。
exe, in, out 文件可删可不删。

提交上去的代码一定一定记得文件 OI。

点击查看代码

int main() {
    freopen("xxx.in", "r", stdin);
    freopen("xxx.out", "w", stdout);
    ...
}

除非有 100% 的把握写出 100pts 的代码，否则先写部分分代码。
题目背景虽然很废话，但是一定要读，中间可能会穿插一些重要信息。
不要被题目的长度吓倒，不要着急写代码，先读懂题目再说。
草稿纸每道题要分区明确，以便之后好检查对错。
~~不要玩扫雷或蜘蛛卡牌~~
最后 10 分钟检查文件 OI。
记得带水补充饱食度。
评测机抽风可以给 CCF 申请重测。（byd 还要钱）

数据范围	时间复杂度	可能用到的算法
$n <= 12$	$O(n!)$	全排列
$n <= 20$	$O(2^n \times n\ (\times n)) $	状压 DP、折半搜索、朴素dfs
$n <= 800$	$O(n^3)$	Floyd、区间 DP
$n <= 5000$	$O(n ^ 2 \times log\ n)$	DP
$n <= 10^5$	$O(n\ log\ n)$	线段树、树状数组
$n <= 10^7$	$O(n)$	线性算法
$n <= 10 ^ {12}$	$O(\sqrt{n})$	思维题
$more$	$O(log\ n, 1)$	思维题

D1 Competition

戳我进入提高 Day1 比赛

戳我进入普及 Day1 比赛

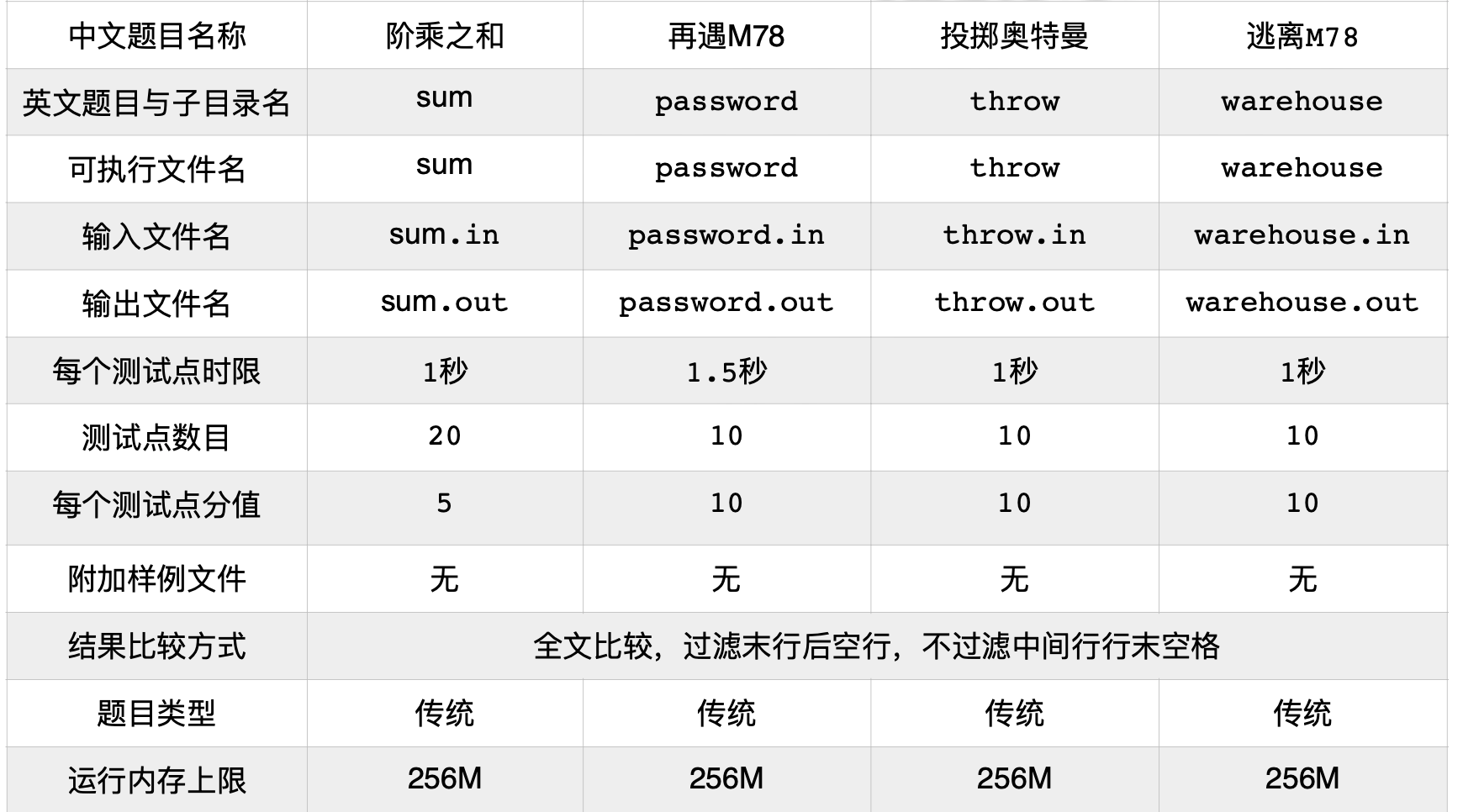
赛时成绩：100 + 20 + 0 + 60 = 180

T1 sum

题目大意
给定一个 $n \times n$ 的 01 矩阵 $A$，求 $\max\limits_{\forall i \in [1, n] ,j \in [1, m]}{\sum\limits_{x = 1} ^ {i - 1} A_{x, j} + \sum\limits_{x = i + 1} ^ {n} A_{x, j} + \sum\limits_{y = 1} ^ {j - 1} A_{i, y} + \sum\limits_{y = j + 1} ^ {m} A_{i, y} + A_{i, j} \times 2}$。
满足 $100\%$ 数据，$1 \le n, m \le 10^2$。

没什么好讲的，数据范围小枚举十字架中间点加和最大值即可，时间复杂度 $O(n ^ 3)$。

点击查看代码

#include <bits/stdc++.h>

#define endl '\n'
#define int long long
#define lowbit(x) x & (-x)

using namespace std;
const int N = 1e2 + 5;

int n, m;
int a[N][N];

signed main() {
    freopen("sum.in", "r", stdin);
    freopen("sum.out", "w", stdout);
    cin >> n >> m;
    for(int i = 1;i <= n; ++i) 
    	for(int j = 1;j <= m; ++j) 
    		cin >> a[i][j];
    int ans = 0, sum;
    for(int i = 1, x, y;i <= n; ++i) {
    	for(int j = 1;j <= m; ++j) {
    		x = i - 1, y = j - 1, sum = 0;
    		while(x >= 1) sum += a[x--][j];
    		while(y >= 1) sum += a[i][y--];
    		x = i + 1, y = j + 1;
    		while(x <= n) sum += a[x++][j];
    		while(y <= m) sum += a[i][y++];
    		ans = max(ans, sum + 2 * a[i][j]);
		}
	}
	cout << ans << endl;
	return 0;
}

T2 password

题目大意
有一个以数列的形式给出的 $n \times n$ 的矩阵 $A$，即大小为 $n \times n$ 的序列 $A$，其中 $A_{i \times n + j} = gcd(b_i, b_j)\ 0 \le i, j \le n$，其中 $b$ 是一个大小为 $n$ 的单调递减的序列。现需求出序列 $b$。
$20\%$ 数据满足特殊性质：$\forall i \in [0, n), j \in [0, n), gcd(b_i, b_j) = 1$。
$100\%$ 数据满足 $n \le 10^3, A_i \le 10^9$。

因为 $gcd(a, b) \leq a, b$，所以我们可以知道 $b$ 的第一个数一定是 $A$ 的最大值，第二个数一定是 $A$ 的次大值。

接下来第 $i$ 个数就是将之前 $b_j, j \in [1, i - 1]$ 两两互相配对的最大公因子于 $A$ 中删掉两个后，$A$ 序列中的最大值。

为什么是两个呢？因为 $b_x$ 和 $b_y$ $x \ne y$ 在 $A$ 中恰好会配对两次，至于自己与自己配只用删除一次。

总时间复杂度为 $O(n^2 log n)$。

点击查看代码

#include <bits/stdc++.h>

#define endl '\n'
#define int long long
#define lowbit(x) x & (-x)

using namespace std;
const int N = 1e3 + 5;

int n, nn;
int a[N * N], b[N];
unordered_map<int, int> to;

int gcd(int x, int y) { return (y? gcd(y, x % y) : x); }

signed main() {
    freopen("password.in", "r", stdin);
    freopen("password.out", "w", stdout);
    cin >> n;
    for(int i = 1;i <= n * n; ++i) cin >> a[i], ++to[a[i]];
    sort(a + 1, a + n * n + 1, greater<int>());
    nn = unique(a + 1, a + n * n + 1) - a - 1;
    for(int i = 1, f = 1;i <= n; ++i) {
    	while(to[a[f]] <= 0 && f < nn) ++f; b[i] = a[f], --to[b[i]];
    	for(int j = 1;j < i; ++j) to[gcd(b[i], b[j])] -= 2;
	}
	for(int i = 1;i <= n; ++i) cout << b[i] << " ";
	return 0;
}

T3 throw

题目大意
给定两个三元组 $(a, b, c), (d, e, f)$，要求这两个三元组完全重合。每次操作先选定两个点 $x, y$，让 $x \gets 2y - x$，须满足 $x$ 向 $y$ 方向跳跃中任何时刻两点间都不能出现另外一个点。上文提到的重合只要求 $(a, b, c)$ 在 $(d, e, f)$ 中都具有相同的数。
$20\%$ 数据满足，$|a, b, c, d, e, f| \le 10$。
$40\%$ 数据满足，$|a, b, c, d, e, f| \le 10^4$。
$100\%$ 数据满足，$|a, b, c, d, e, f| \le 10^9$。

T4 warehouse

题目大意
给定一个 $n$ 个点，$m$ 条边的带权无向图以及 $q$ 次询问，每次询问有一个正整数 $k$，需求最少将图分成几块使得每块不含有边权小于 $k$ 的边。
$30\%$ 数据满足，$n, m, q \le 10^3$。
$60\%$ 数据满足，$n, m, q \le 10^4$。
$100\%$ 数据满足，$n, m, q \le 10^5$。

考虑贪心，先求得图的最大生成树，我们在这个树上走就能使得走过所有的点且最大化通行人数，那么第一个大于等于 $k$ 的树边是树边集中第几小，这就是答案。

点击查看代码

#include <bits/stdc++.h>

#define endl '\n'
#define int long long
#define lowbit(x) x & (-x)

using namespace std;
const int N = 1e6 + 5;

namespace DSU {
	int fa[N];
	void merge(int x, int y) { fa[x] = y; }
	void init(int n) { for(int i = 1;i <= n; ++i) fa[i] = i; }
	int find(int x) { return fa[x] == x? x : fa[x] = find(fa[x]); }
} using namespace DSU;

int n, m, q;
int road[N];
struct Edge {
	int u, v, w;
	bool operator< (const Edge &b) const {
		return w > b.w;
	}
}e[N];

signed main() {
    freopen("warehouse.in", "r", stdin);
    freopen("warehouse.out", "w", stdout);
    cin >> n >> m >> q, init(n);
    for(int i = 1;i <= m; ++i) 
    	cin >> e[i].u >> e[i].v >> e[i].w;
    int l = 0; sort(e + 1, e + m + 1);
    for(int i = 1;i <= m; ++i) 
    	if(find(e[i].u) != find(e[i].v)) 
    		merge(find(e[i].u), find(e[i].v)),
    		road[++l] = e[i].w;
    reverse(road + 1, road + l + 1);
    while(q--) {
    	static int k; cin >> k;
    	cout << lower_bound(road + 1, road + l + 1, k) - road << endl;
	}
	return 0;
}

Day2

D2 Note

二分答案

在此之前需满足二分性，假设答案，看答案是否满足条件。

精度枚举

二分或三分

具有单调性的题目

check 函数

字符串哈希

将某个字符串拆成 $base$ 进制的数，若产生冲突考虑挂链哈希或二次探测，可用于字符串的匹配等问题。

字典树（trie 树）

先放一张图：

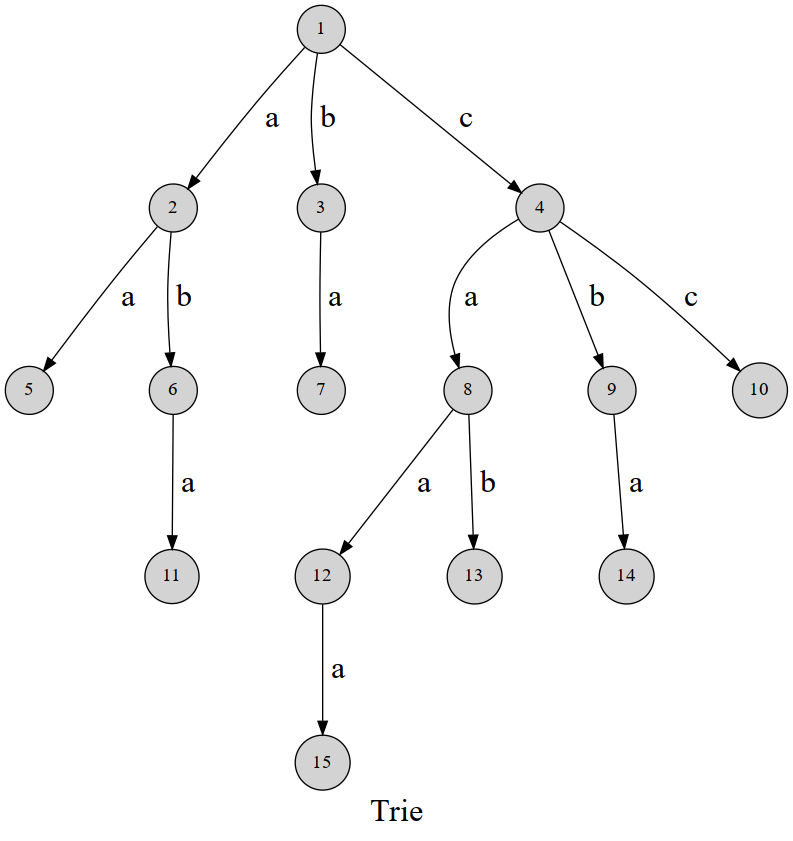
可以发现，这棵字典树用边来代表字母，而从根结点到树上某一结点的路径就代表了一个字符串。举个例子，$ 1\to4\to 8\to 12$ 表示的就是字符串 caa。

trie 的结构非常好懂，我们用 $\delta(u,c)$ 表示结点 $u$ 的 $c$ 字符指向的下一个结点，或着说是结点 $u$ 代表的字符串后面添加一个字符 $c$ 形成的字符串的结点。（$c$ 的取值范围和字符集大小有关，不一定是 $0\sim 26$。）

有时需要标记插入进 trie 的是哪些字符串，每次插入完成时在这个字符串所代表的节点处打上标记即可。

字典树最基础的应用——查找一个字符串或字符串的前缀是否在「字典」中出现过或出现次数。

以上摘自「https://oi-wiki.com」

例题 Luogu P2580 于是他错误的点名开始了

简单的字典树应用题。

点击查看代码

#include <bits/stdc++.h>

#define endl '\n'
#define int long long
#define lowbit(x) x & (-x)

using namespace std;
const int N = 5e5 + 5;

int n, tot;
int nxt[N][26], value[N];

void inset(string a) {
	int now = 0;
	for(const auto &c : a) {
		if(!nxt[now][c - 'a']) 
			nxt[now][c - 'a'] = ++tot;
		now = nxt[now][c - 'a'];
	} value[now] = 1;
}

int find(string a) {
	int now = 0;
	for(const auto &c : a) {
		if(!nxt[now][c - 'a']) 
			return 0;
		now = nxt[now][c - 'a'];
	} 
	if(value[now] == 1) 
		return value[now] = -1, 1;
	else if(value[now] == -1)
		return -1;
	else 
		return 0;
}

signed main() {
//    freopen("xxx.in", "r", stdin);
//    freopen("xxx.out", "w", stdout);
	string str;
	cin >> n;
	while(n--) 
		cin >> str, inset(str);
	cin >> n;
	while(n--) {
		cin >> str;
		if(find(str) == 1) puts("OK");
		else if(find(str) == -1) puts("REPEAT");
		else puts("WRONG");
	}
	return 0;
}

求最长回文子串问题

二分 + 哈希

可以清楚的回文子串具有二分性。

我们可以在每个字母之间添加一个特殊字符，使得所有奇回文串和偶回文串都变成奇回文串，并预处理字符串的前后缀哈希值。

随后枚举中间点，并二分最长扩展长度、利用哈希 $O(1)$ 地比较两边是否相等。

最终时间复杂度为 $O(n log n)$

Manacher

Manacher 求最长回文子串
 Manacher 求回文子串的对数

最终时间复杂度为 $O(n)$，为线性做法。

D2 Competition

戳我进入提高组比赛

赛时成绩：100 + 0 + 100 + 0 = 200

T1 number

题目大意
给定一个长度为 $n$ 的序列 $A$，要求你找出一种排列，使得 $\max\limits_{i \in [1, \frac{n}{2}]}\ A_{2i - 1} + A_{2i}) $ 最小化。
$n \le 10^4, a_i \le 10^9$ 且 $n$ 为偶数。

考虑贪心，很明显为了使其最小化，我们应当让第 $1$ 小的数和第 $1$ 大的数加在一起，第 $2$ 小的数和第 $2$ 大的数加在一起……，最后取最大值，时间复杂度 $O(n log n)$。

点击查看代码

#include <bits/stdc++.h>

#define endl '\n'
#define int long long
#define lowbit(x) x & (-x)

using namespace std;
const int N = 1e6 + 5;

int n;
int a[N];

signed main() {
	cin >> n;
	for(int i = 1;i <= n; ++i) cin >> a[i];
	sort(a + 1, a + n + 1);
	int l = 1, r = n, ans = -(1ll << 60);
	while(l < r) ans = max(ans, a[l++] + a[r--]);
	cout << ans << endl;
	return 0;
}

T2 multiset

题目大意
你有一只生物初始能量为 $0$，在每一天可以有三种操作：1.分裂出两个能量之和为自己的同种生物。 2.自己能量加 $1$。 3. 什么也不干。
给定生物最终的形态，求最少花费的时间。（注意在任何时刻，生物能量必须为非负整数）。
$10\%$ 数据满足，$n \le 10, m \le 10$。
$30\%$ 数据满足，$n \le 50, m \le 100$。
$50\%$ 数据满足，$n \le 10^3, m \le 10^4$。
$100\%$ 数据满足，$n \le 10^6, m \le 10^6$。

正难则反的思想，考虑利用最终样子倒推，则在其他生物给自己能量减 $1$ 时，其他生物可以借此同时合并，但记住每次合并至少会留下一个。

点击查看代码

#include <bits/stdc++.h>

#define endl '\n'
#define int long long
#define lowbit(x) x & (-x)

using namespace std;
const int N = 1e6 + 5;

int n;
int a[N];

signed main() {
	cin >> n;
	for(int i = 1;i <= n; ++i) cin >> a[i];
	sort(a + 1, a + n + 1);
	int cnt = 0;
	for(int i = 1;i <= n; ++i) 
		cnt = max(1ll, cnt >> (a[i] - a[i - 1])), ++cnt;
	if(cnt) a[n] += (cnt >> 1) + (cnt & 1); cout << a[n] << endl;
	return 0;
}

T3 road

题目大意
给定一个 $n$ 个点 $m$ 条边的有向图，且 $m$ 条边的编号依次为 $1 \sim m$，我们要将图分成若干个子图，使得子图每条边在母图编号连续、且子图不存在一条 $1$ 到 $n$ 的路径。咋此基础上，要使子图个数最少。
$30\%$ 数据满足，$n \le 100, m \le 500$。
$60\%$ 数据满足，$n \le 5000, m \le 20000$。
$100\%$ 数据满足，$n \le 100000, m \le 500000$。

考虑二分，轻松可以想到这个联通具有二分性，则我们在上一段子图最后一条边到第 $m$ 条边中二分出当前子图的最后一条边，时间复杂度严格小于 $O(ans \times log m \times m)$。

点击查看代码

#include <bits/stdc++.h>

#define endl '\n'
#define lowbit(x) x & (-x)

using namespace std;
const int N = 2e5 + 5;
const int M = 5e5 + 5;

int n, m;
int ans, cnt;
int u[M], v[M], vis[N];
vector<int> G[N];

bool dfs(int u) {
	vis[u] = cnt;
	if(u == n) return 1;
	for(const auto &v : G[u]) {
		if(vis[v] == cnt) 
			continue;
		if(dfs(v)) return 1;
	} return 0;
}

signed main() {
	cin >> n >> m;
	for(int i = 1;i <= m; ++i) 
		cin >> u[i] >> v[i];
	for(int st = 1;st <= m; ++ans) {
		int l = st, r = m, mid, res = st;
		while(l <= r) {
			++cnt;
			mid = (l + r) >> 1;
			for(int i = st;i <= mid; ++i) 
				G[u[i]].emplace_back(v[i]);
			if(!dfs(1)) {
				for(int i = st;i <= mid; ++i) G[u[i]].clear();
				l = mid + 1, res = mid;
			} else {
				for(int i = st;i <= mid; ++i) G[u[i]].clear();
				r = mid - 1;
			}
		} st = res + 1; if(st > m) break;
	} cout << ans + 1 << endl;
	return 0;
}

其实这里蒋老还讲了 $O(\frac{ans \times log m \times \sqrt{m}}{2})$、$O(m log m)$ 的做法，不过我不会，也没让我写。 \kx

T4 binary

~~合着这题目标题纯迷惑人~~

题目大意
有 $n$ 个点，假设小明藏在 $x$ 号点，则 $1 \sim x - 1$ 的点都会留下踪迹，每个点的搜查时间为 $t_i$，求最坏情况下的最少时间。
$30\%$ 数据满足，$n \le 600$。
$60\%$ 数据满足，$n \le 1300$。
$100\%$ 数据满足，$n \le 2000, t_i \le 10^6$。

遇到最小值最大或最大值最小相关问题，一般不是二分就是 DP。

考虑区间 DP，设 $f_{i, j}$ 为 $i \sim j$ 号点间的答案，则转移方程为

\[f_{i, j} = \min\limits_{k \in [i, j]} t_k + max(f_{i, k - 1}, f_{k + 1, j}) \]

时间复杂度为 $O(n ^ 3)$，很明显过不了此题。

点击查看代码

#include <bits/stdc++.h>

#define endl '\n'
#define int long long
#define lowbit(x) x & (-x)

using namespace std;
const int N = 3e3 + 5;

int n, a[N], f[N][N];

signed main() {
	memset(f, 0x3f, sizeof f);
    cin >> n;
    for(int i = 1;i <= n; ++i) cin >> a[i];
   	for(int i = 1;i <= n; ++i) f[i][i - 1] = f[i][i] = f[i + 1][i] = a[i];
   	for(int len = 2;len <= n; ++len) {
   		for(int i = 1;i <= n; ++i) {
   			int j = i + len - 1;
			for(int k = i;k <= j; ++k)	
				f[i][j] = min(f[i][j], a[k] + max(f[i][k - 1], f[k + 1][j]));
		}
    } cout << f[1][n] << endl;
	return 0;
}

对于 $60\%$ 数据而言，考虑二分 + 线段树优化，因为 $f$ 数组具有单调性，因此利用二分求出分隔点，并构造 $n$ 个线段树来维护最小值，时间复杂度 $O(n^2 log n)$。

对于 $100\%$ 数据而言，考虑单调栈优化，时间复杂度 $O(n^2)$，~~具体实现方法我不会~~。

Day3

D3 Note

DP:

状态设计：数组定义
转移方程：状态运算

空间复杂度：状态设计

时间复杂度：转移 * 状态

空间复杂度优化：滚动数组、降维

时间复杂度优化：降维、数据结构、数学方法

暴力搜索-> 暴力DP -> 降维 -> 计算时空

DP 分类：

线性 DP：顾名思义。

区间 DP：区间 DP

DAG DP：DAG DP

树形 DP：树形 DP

额外补充

特殊例题，类似于有后效性，或子节点与父节点有关：

求树上一共有多少条路径：

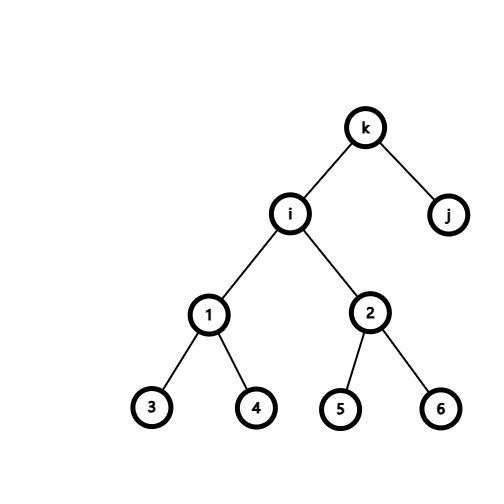
如图，$i, j$ 分别为 $k$，令 $f_{i, 0}$ 表示以 $i$ 号节点为根节点的子树中路径个数，$f_{i, 1}$ 表示以 $i$ 号节点为根节点的子树中点向外走的路径个数。
则有状态转移方程：

\[\begin{array}{c} f_{k, 0} = f_{i, 0} + f_{j, 0} + f_{i, 1} \times f_{j, 1} \\ f_{k, 1} = f_{i, 1} + f_{j, 1} \end{array} \]

换根 DP

插头 DP：插头 DP

背包 DP：背包 DP

状压 DP：状压 DP

数位 DP：数位 DP

Day 4

D4 Note

启发式合并：小并大。

数据结构：空间换时间

动态线段树：动态线段树

线段树合并：线段树合并

Splay

方法论：

DP 方法论

先想想搜索如何写。
再通过升维或降维改成 DP。
DP 优化：单调性（单调栈、单调队列）、区间性（线段树）、矩阵加速
状态定义定义较小的。
只要状态定义固定，都可以用矩阵加速 DP。

Day5

D5 Note

要学会变通，找方案数要学会找正确枚举对象

压位

打表：

图论方法论

最短路径生成树、最小生成树。

正难则反
最小最大，最大最小，不是二分就是 DP

posted @ 2024-10-01 09:31 Quatry 阅读(29) 评论(1) 收藏举报

刷新页面返回顶部

数据范围	时间复杂度	可能用到的算法
\(n <= 12\)	\(O(n!)\)	全排列
\(n <= 20\)	$O(2^n \times n\ (\times n)) $	状压 DP、折半搜索、朴素dfs
\(n <= 800\)	\(O(n^3)\)	Floyd、区间 DP
\(n <= 5000\)	\(O(n ^ 2 \times log\ n)\)	DP
\(n <= 10^5\)	\(O(n\ log\ n)\)	线段树、树状数组
\(n <= 10^7\)	\(O(n)\)	线性算法
\(n <= 10 ^ {12}\)	\(O(\sqrt{n})\)	思维题
\(more\)	\(O(log\ n, 1)\)	思维题

Likeyy

国庆集训笔记

Day1

D1 Note

D1 Competition

Day2

D2 Note

二分答案

字符串哈希

字典树（trie 树）

例题 Luogu P2580 于是他错误的点名开始了

求最长回文子串问题

D2 Competition

Day3

D3 Note

Day 4

D4 Note

方法论：

Day5

D5 Note

公告