多项式乘法
忘记板子怎么背了,重新仔细学一下。
两个 \(n\) 项式相乘,暴力是 \(O(n^2)\) 的,非常劣。但是看上去没什么优化前途,考虑改变多项式的表达方式,于是点值表示法应运而生。
点值表示法的思想是向这个 \(n\) 项式带入 \(n\) 个特意构造的不同的自变量的值,得到 \(n\) 个函数关系,它与这个 \(n\) 项式一一对应。
它的优缺点相当显著:善于做两个多项式的加减乘各种运算,因为对于相同的自变量,直接对多项式的值作运算即可;但是他不好和西数表示法互相转换,所得到的点值不好用也不直观。于是 FFT 与 IFFT 一起来解决这个棘手的问题。
我想了很久也没有想通,为什么 Cooley&Tukey 能引入这么抽象的东西来解决这个问题,甚至在欧洲世界还在全员反法的时候高斯这个b已经发明过了,所以需要扔一点前置知识。
复数
复数在实数上扩充了虚数,是形如 \(a+bi\) 的数。\(i\) 是虚数单位,有着 \(i^2=-1\) 的强制性限制(就是因为没有 \(\sqrt{-1}\) 才发明的东西),\(a\) 与 \(b\) 是两个实数,分别为该复数的实部与虚部(一个单独为实数,一个乘 \(i\) 为虚数)
由于加入了虚数这一维度,表示复数的工具由数轴变为了平面直角坐标系。一个复数的 \(x\) 坐标表示实部,\(y\) 坐标表示虚部。
又因为虚数现在正在平面直角坐标系上,那么它就能表示一个向量。向量的方向,由 \(x\) 轴正半轴逆时针旋转使其与复数向量而得的角为该复数的幅角;向量的长度,即与坐标轴原点 \(O\) 的距离,即 \(\sqrt{a^2+b^2}\),为该复数的模长。
设参与运算的两复数 \(z_1=a+bi, z_2=c+di\)。
加减法要运用向量平行四边形法则(实部虚部分别加起来)。\(z_1\pm z_2=(a\pm c)+(b\pm d)i\)。
乘法更加特殊。可以总结为模长相乘,幅角相加,\(z_1*z_2=ac-bd+(ad+bc)i\)。
单位根
有了乘法美妙的幅角相加性质,可以按角度选点。为了避免模长相乘带来的麻烦,不如直接令模长等于 \(1\),即在单位圆上按角度找点。
比如要找 \(n\) 个点,我们不如把这单位圆平分了。幅角为 \(\frac{2\pi}{n}\) 的复数为 \(\cos \frac{2\pi}{n}+i\sin \frac{2\pi}{n}\),我们叫它 \(n\) 次单位根 \(\omega_n\)。
因为复数相乘,幅角相加,所以 \(\omega_n^k\) 可以直接 \(k\) 倍幅角,则它为 \(\cos \frac{2\pi k}{n}+i\sin \frac{2\pi k}{n}\)。
单位根由于在复数单位圆上,也有许多美妙的性质(以下默认 \(2\mid n\))
\(\omega_n^n=\omega_n^0=1\),一个转一圈回来了,一个动都没动。
\(\omega_n^{\frac{n}{2}}=-1\),又有 \(\omega_n^k=-\omega_n^{k\pm\frac{n}{2}}\),转了半圈到 \(x\) 轴负半轴上了。
\(\omega_{2n}^{2k}=\omega_n^k\),前者只是分得更细,对答案没有影响。因此它也可以扩展为 \(\omega_{pn}^{pk}=\omega_n^k\)( \(p\) 为正整数)
前置知识结束。
FFT
给定一个 \(n\) 项式 \(F(x)=\sum\limits_{i=0}^{n-1} a_i x^i\),快速求他对于所有 \(\omega_n^i\) 的点值表示法。
因为单位根的一些性质需要多项式项数总是偶数,普通的数不方便,直接把 \(n\) 扩大到 \(2\) 的次幂,系数用 \(0\) 补全。
\(F(x)\) 展开 \(a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1}\)
我们想要以类似递归的方式优化复杂度,所以需要把系数分成两半,再特殊考虑。按下标奇偶分组,得到
\(F_0(x)=a_0+a_2x+a_4x^2+\dots+a_nx^{\frac{n}{2}-1}\),
\(F_1(x)=a_1+a_3x+a_5x^2+\dots+a_{n-1}x^{\frac{n}{2}-1}\)
显然有 \(F(x)=F_0(x^2)+xF_1(x^2)\)。
带入单位根 \(\omega_n^k\) 和 \(\omega_n^{k+\frac{n}{2}}\),有
\(F(\omega_n^k)=F_0(\omega^{2k}_n)+\omega^{k}_nF_1(\omega^{2k}_n)\)
\(F(\omega_n^{k+\frac{n}{2}})=F_0(\omega^{2k+n}_{n})+\omega_n^{k+\frac{n}{2}}F_1(\omega^{2k+n}_{n})=F_0(\omega^{2k}_n)-\omega^{k}_nF_1(\omega^{2k}_n)\)
它们之间仅有系数符号不同,只需要求出 \(F_0(\omega^{2k}_n)\) 和 \(F_1(\omega^{2k}_n)\) 即可求出以上两个值。
又因为 \(\omega^{2k}_n=\omega^k_{\frac{n}{2}}\),成功地将要求的数的个数减半。同样地, \(F_0\) 和 \(F_1\) 也可以分别通过类似方法求。复杂度 \(O(n\log n)\)。
IFFT
已知一个 \(n\) 项式对于所有 \(\omega_n^i\) 的点值表示法,求原多项式的各项系数。
令这些点值为 \(p\),即 \(p_i=F(\omega_n^i)\)。
由于系数转点值时乘了个 \(\omega_n^k\),我们尝试对应地乘上 \(\omega_n^{-k}\) 以消除单位根对点值的影响,推出原系数。
所以我们对 \(p\) 再做一次类似系数传点值的操作,一样 FFT,只是放进去的单位根顺序改成了 \(\omega_n^{-k}\)。令再次得到的点值为 \(q\)。
推一下 \(q\) 和 \(a\) 的关系。
\(q_i=\sum\limits_{j=0}^{n-1}f(\omega^j_n)(\omega^{-i}_n)^j\) 定义
\(=\sum\limits_{j=0}^{n-1}(\sum\limits_{k=0}^{n-1}a_k\omega^{jk}_n)\omega^{-ij}_n\) 展开 \(f\) 函数
\(=\sum\limits_{j=0}^{n-1}(\sum\limits_{k=0}^{n-1}a_k\omega_n^{j(k-i)})\) 把用于消除的单位根扔进去
\(=\sum\limits_{k=0}^{n-1}a_k[\sum\limits_{j=0}^{n-1}(\omega_n^{k-i})^j]\) 想要把 \(a_k\) 扔到外面,调换求和顺序
研究一下中括号里的函数 \(g(x)=\sum\limits_{i=0}^{n-1}x^i\)。
等比数列求和得 \(g(x)=\frac{x^n-1}{x-1}\)。由于给到 \(g\) 的 \(x\) 是 \(n\) 次单位根,所以 \(x^n\) 一定等于 \(1\),分子一定为 \(0\)。
如果 \(x-1=0\),即 \(x=1\) 时,等比数列求和得式无意义,但 \(g(1)=n\)。否则,\(g(x)=0\)。\(g\) 函数仅在 \(x=1\) 时答案非 \(0\)。
所以只有在 \(k=i\) 时,中括号内数不为 \(0\),且为 \(n\)。
\(q_i=a_in\),\(a_i=\frac{q_i}{n}\)。
系数反推成功。
蝴蝶变换
现在这个算法的时空常数拉满了,奇偶分组开数组又耗空间还耗时,递归实现常数直接飞升。由于这个递归是一个小区间到大区间的一个合并过程,可以改变原系数序列的顺序,合并相邻两个分组区间,就可以不用新开数组、不用递归了。
顺序改变参考下图:
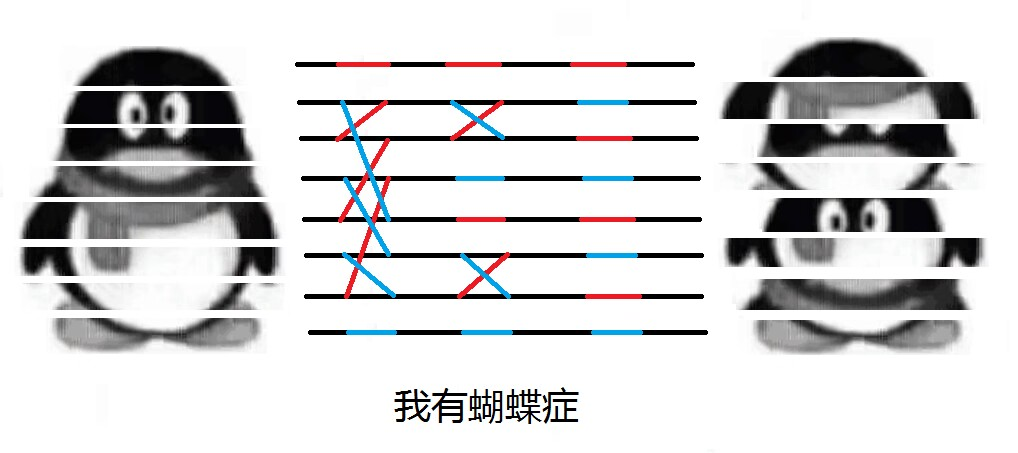
红线为偶,蓝线为奇。
0 1 2 3 4 5 6 7 \(\rightarrow\) 0 2 4 6 1 3 5 7 \(\rightarrow\) 0 4 2 6 1 5 3 7。
改为二进制看一下:
000 001 010 011 100 101 110 111(变换前)
000 100 010 110 001 101 011 111(变换后)
没错,就是二进制翻转。
那么如何得到 \([0,n)\) 之间数的二进制翻转呢?
考虑递推。因为 \(n\) 右移 \(1\) 的值已经知道,只需要删去右移一翻转末尾多出的 \(0\),并在最高位加上原数最低位的值即可。
即 rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (__lg(n) - 1))。
举个例子:
110101(原数)
011010(右移1位)
010110(二进制翻转)
001011(删去右移1多出的末位0)
101011(补上原数最后一位)
Code
// STOOOOOOOOOOOOOOOOOOOOOOOOO hzt CCCCCCCCCCCCCCCCCCCCCCCORZ
#include <algorithm>
#include <cmath>
#include <iomanip>
#include <iostream>
#include <numeric>
#include <vector>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
constexpr int kN = (1 << 22) + 1;
const double kPi = acos(-1);
struct Complex {
double x, y;
Complex(double _x = 0, double _y = 0) { x = _x, y = _y; }
Complex operator+(const Complex z) const { return {x + z.x, y + z.y}; }
Complex operator-(const Complex z) const { return {x - z.x, y - z.y}; }
Complex operator*(const Complex z) const { return {x * z.x - y * z.y, y * z.x + x * z.y}; }
} a[kN], b[kN];
int p, q, n, rev[kN];
void FFT(Complex *a, int t) {
for (int i = 0; i < n; i++) {
i < rev[i] && (swap(a[i], a[rev[i]]), 0);
}
for (int m = 2; m <= n; m *= 2) {
Complex wn = {cos(2 * kPi / m), t * sin(2 * kPi / m)};
for (int i = 0; i < n; i += m) {
Complex c = {1, 0};
for (int j = 0; j < m / 2; j++, c = c * wn) {
Complex x = a[i + j], y = c * a[i + j + m / 2];
a[i + j] = x + y, a[i + j + m / 2] = x - y;
}
}
}
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> p >> q;
for (int i = 0; i <= p; i++) {
cin >> a[i].x;
}
for (int i = 0; i <= q; i++) {
cin >> b[i].x;
}
for (n = 1; n <= p + q; n *= 2) {
}
for (int i = 0; i < n; i++) {
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (__lg(n) - 1));
}
FFT(a, 1), FFT(b, 1);
for (int i = 0; i <= n; i++) {
a[i] = a[i] * b[i];
}
FFT(a, -1);
for (int i = 0; i <= p + q; i++) {
cout << int(a[i].x / n + 1e-3) << ' ';
}
return 0;
}
NTT
为什么 FFT 时空常数起飞?其主要原因在于点值带入的单位根复数每次都给个 pair<double, double>,还有大量的三角函数,误差也拉满。怎么改变这个问题呢?或者说,怎么替代掉有着这么多坏处的单位根呢?
原根
对于数 \(a\) 和模数 \(p\),有一个最小的正整数 \(k\),使得 \(a^k\equiv 1\ (mod\ p)\),则称 \(k\) 是 \(a\) 模 \(p\) 意义下的阶,写作 \(\delta_p(a)=k\)。
对于一个模数 \(p\),有一个数 \(a\) 满足 \(\delta_p(a)=\phi(p)\),则称 \(a\) 是 \(p\) 的一个原根。
令 \(n\) 是一个大于 \(1\) 的 \(2\) 的幂,我们引入模数 \(p\) 来构造原根,下面将用 \(p\) 的原根 \(g\) 来一步步代替单位根。
令 \(g_n=g^{\frac{p-1}{n}}\)(此举需要 \(p-1\) 被 \(n\) 整除)
我们用到了的单位根的性质有:
- \(\omega_n^n=\omega_n^0=1\)。\(g_n^n=g^{p-1}=1\),\(g_n^0\) 显然为 \(1\)。
- \(\omega_n^{\frac{n}{2}}=-1\)。\(g_n^{\frac{n}{2}}=\pm\sqrt{g_n^n}=\pm 1\)。又因为 \(\delta_p(a)=\phi(p)>\frac{n}{2}\),所以 \(g_n^{\frac{n}{2}}\neq 1\),只能等于 \(-1\)。
- \(\omega_{an}^{ak}=\omega_n^k\)。\(g_{an}^{ak}=g^{\frac{ak(p-1)}{an}}=g^{\frac{k(p-1)}{n}}=g_n^k\)。
- 单位根两两不同。若存在 \(1\leq i<j\leq \phi(p)\),使得 \(g^i \equiv g^j\ (mod\ p)\),则 \(g^{j-i}\equiv 1\ (mod\ p)\),因为 \(j-i<\phi(p)\),与 \(\delta_p(a)=\phi(p)\) 矛盾。
于是飞舞单位根被完全替代了。
Code
// STOOOOOOOOOOOOOOOOOOOOOOOOO hzt CCCCCCCCCCCCCCCCCCCCCCCORZ
#include <algorithm>
#include <iostream>
#include <numeric>
#include <vector>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
constexpr int kN = (1 << 22) + 1, kP = 998244353, kG = 3, iG = 332748118;
int P(int a, int b) {
int ret = 1;
for (; b > 0; b /= 2) {
if (b & 1) {
ret = 1ll * ret * a % kP;
}
a = 1ll * a * a % kP;
}
return ret;
}
int a[kN], b[kN];
int p, q, n, rev[kN];
void NTT(int *a, int t) {
for (int i = 0; i < n; i++) {
i < rev[i] && (swap(a[i], a[rev[i]]), 0);
}
for (int m = 2; m <= n; m *= 2) {
int gn = P((t ? kG : iG), (kP - 1) / m);
for (int i = 0; i < n; i += m) {
int c = 1;
for (int j = 0; j < m / 2; j++, c = 1ll * c * gn % kP) {
int x = a[i + j], y = 1ll * c * a[i + j + m / 2] % kP;
a[i + j] = (x + y) % kP;
a[i + j + m / 2] = (x - y + kP) % kP;
}
}
}
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> p >> q;
for (int i = 0; i <= p; i++) {
cin >> a[i];
}
for (int i = 0; i <= q; i++) {
cin >> b[i];
}
for (n = 1; n <= p + q; n *= 2) {
}
for (int i = 0; i < n; i++) {
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (__lg(n) - 1));
}
NTT(a, 1), NTT(b, 1);
for (int i = 0; i <= n; i++) {
a[i] = 1ll * a[i] * b[i] % kP;
}
NTT(a, 0);
for (int i = 0, ivn = P(n, kP - 2); i <= p + q; i++) {
cout << 1ll * a[i] * ivn % kP << ' ';
}
return 0;
}
那如果最后乘出来的系数被取到模,改变了真实值了,怎么办呢?可以用多个质数和它的原根,得出取模后结果然后 CRT。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号