ARC175 补
A - Spoon Taking Problem
\(n\) 个人围圆桌吃饭,人和人之间放一个勺子。每个人有唯一惯用手,按排列 \(p\) 顺序拿勺子时,优先选择惯用手侧。告诉你部分人的惯用手,问如果所有人都能拿到勺子,未给定人的惯用手有多少种可能。
Solution
显然第一个人的惯用手决定了以后每个人拿勺子的方向。不妨设第一个人惯用右手。惯用手给定容易考虑。考虑不给定,当前考虑到第 \(i\) 个人时,没勺子就无解,两边都有则惯用手固定,同时惯用手给定。若只有一个,则无论惯用手都只能选择这一个,方案数乘二。
\(\\\)
Code
// STOOOOOOOOOOOOOOOOOOOOOOOOO hzt CCCCCCCCCCCCCCCCCCCCCCCORZ
#include <algorithm>
#include <iostream>
#include <numeric>
#include <vector>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
constexpr int kN = 2e5 + 1, kP = 998244353;
int n, p[kN], t[kN];
string s;
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> p[i];
}
cin >> s;
LL L = 1, R = 1;
for (int i = 1; i <= n; i++) {
int j = p[i] - 1;
if (t[p[i] % n + 1]) {
L = L * (1 + (s[j] == '?')) % kP;
} else if (s[j] == 'R') {
L = 0;
}
if (t[j ? j : n]) {
R = R * (1 + (s[j] == '?')) % kP;
} else if (s[j] == 'L') {
R = 0;
}
t[p[i]] = 1;
}
cout << (L + R) % kP << '\n';
return 0;
}
B - Parenthesis Arrangement
给定一个长度为 \(2n\) 的括号序列,每次操作可以花费 \(a\) 的代价交换两字符,或花费 \(b\) 的代价更改一字符,求使其变为合法括号序列的最小代价。
Solution
删去可以配对的,剩下的随便做。
\(\\\)
Code
// STOOOOOOOOOOOOOOOOOOOOOOOOO hzt CCCCCCCCCCCCCCCCCCCCCCCORZ
#include <algorithm>
#include <iostream>
#include <numeric>
#include <vector>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
int n, a, b;
char ch;
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n >> a >> b;
a = min(a, 2 * b);
int c = 0, mn = 1e9;
for (int i = 1; i <= 2 * n; i++) {
cin >> ch;
c += 2 * (ch == '(') - 1;
mn = min(mn, c);
}
c < 0 && (mn = min(0, mn - c));
cout << 1ll * abs(c) / 2 * b + ((abs(mn) + 1ll) / 2) * a << '\n';
return 0;
}
C - Jumping Through Intervals
给定 \(n\) 个 pair \((l_i, r_i)\),构造一个长度为 \(n\) 的序列 \(a\) 使得其相邻两数差绝对值之和最小,字典序最小,且满足 \(l_i \leq a_i \leq r_i\)。
Solution
暂不考虑区间限制条件。则 \(a_i\) 能尽量与 \(a_{i-1}\) 接近则越好。因为差距越大可能导致答案越劣。那么第一个位置就应该是前缀求交直到交集为空。
考虑怎么优化它的字典序大小。不难发现,如果下一个要往一个方向走,那么提前帮他走一部分是比较优的。但是因为正序枚举没办法知道下一个怎么走,所以倒着考虑。
\(\\\)
Code
// STOOOOOOOOOOOOOOOOOOOOOOOOO hzt CCCCCCCCCCCCCCCCCCCCCCCORZ
#include <algorithm>
#include <iostream>
#include <numeric>
#include <vector>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
#define l first
#define r second
constexpr int kN = 5e5 + 1;
int n;
PII p[kN];
int ans[kN];
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> p[i].l >> p[i].r;
}
auto [l, r] = p[1];
int cur = -1;
for (int i = 2; i <= n; i++) {
cin >> p[i].l >> p[i].r;
if (p[i].r < l) {
cur = l;
break;
} else {
r = min(r, p[i].r);
}
if (p[i].l > r) {
cur = r;
break;
} else {
l = max(l, p[i].l);
}
}
cur == -1 && (cur = l);
for (int i = 1; i <= n; i++) {
cur > p[i].r && (cur = p[i].r);
cur < p[i].l && (cur = p[i].l);
ans[i] = cur;
}
for (int i = n; i >= 2; i--) {
if (ans[i] < ans[i - 1]) {
ans[i - 1] = max(ans[i], p[i - 1].l);
}
}
for (int i = 1; i <= n; i++) {
cout << ans[i] << ' ';
}
return 0;
}
D - LIS on Tree 2
给定一个大小为 \(n\) 的树,求一个 \(n\) 排列 \(p\) 使得按其赋点权,可以使这棵树满足根节点 \(1\) 到每个节点 \(i\) 路径上点权的 LIS 之和等于 \(k\)。
Solution
结论思维题。
结论 1:若 \(k\) 有解,则 \(\min_k\geq n, \max_k\leq \sum dep_i\) 这个结论还挺显然的。
结论 2:\(1 \Rightarrow i\) 路径的 LIS 包含 \(1\Rightarrow fa_i\) 的 LIS 的构造方法一定存在。这个证明包含于具体做法。
通过结论 2,不难发现一个点的 LIS 会继承给整个子树。此时决策一个点权是否计入路径 LIS 里,它对 \(\sum LIS\) 的贡献是 \(siz_i\) 的。
所以这个题变成了,序列 \(siz\) 拼出 \(k\) 的方案,当然 \(siz_1=n\) 必选。可能你会有一些疑问,欸为什么原来上界是 \(dep_i\),这会上界怎么变 \(siz_i\) 了呢?其实每个点的深度之和确实等于每个点的子树大小之和,因为总共有深度这么多个点的子树包含了这个点。可能你还是有疑问:
结论 3:一棵树的所有 \(siz\) 可以拼出 \([1,\sum siz]\) 的所有数。你可以进行手玩或者感性理解。因为 \(siz_i=1+\sum\limits_{v\in son_i} siz_v\),从一开始选一个叶子拼 \(1\) 开始,不断加一,不断进位,可以遍历完所有数。
同时因为结论 3,可以将 \(siz\) 从大到小排序,贪心选择,能选则选。因为这样可以不断减少 \(k\) 的值,就像是枚举位算一个数的某个进制下的数一样。
所以现在知道了哪些点应该在 LIS 里,怎么构造呢?可以让不在 LIS 里的点尽量小,且路径上递减;在 LIS 里的点尽量大,且路径上递增。于是就做完了。
\(\\\)
Code
// STOOOOOOOOOOOOOOOOOOOOOOOOO hzt CCCCCCCCCCCCCCCCCCCCCCCORZ
#include <algorithm>
#include <iostream>
#include <numeric>
#include <vector>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
constexpr int kN = 2e5 + 1;
int n;
LL k;
vector<int> e[kN];
int sz[kN];
bool lis[kN];
vector<PII> v;
void D(int x, int fa) {
sz[x] = 1;
for (auto v : e[x]) {
if (v != fa) {
D(v, x), sz[x] += sz[v];
}
}
v.emplace_back(sz[x], x);
}
int ans[kN], tot;
void A(int x, int fa, bool o) {
o && lis[x] && (ans[x] = ++tot);
for (auto v : e[x]) {
if (v != fa) {
A(v, x, o);
}
}
!o && !lis[x] && (ans[x] = ++tot);
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n >> k;
for (int i = 1, u, v; i < n; i++) {
cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
}
D(1, 0);
if (k < n || k > accumulate(sz + 1, sz + n + 1, 0ll)) {
cout << "No\n";
return 0;
}
cout << "Yes\n";
sort(v.begin(), v.end(), greater<>());
for (auto [siz, i] : v) {
if (k >= siz) {
k -= siz, lis[i] = 1;
}
}
A(1, 0, 0), A(1, 0, 1);
for (int i = 1; i <= n; i++) {
cout << ans[i] << ' ';
}
return 0;
}
E - Three View Drawing
给定一个分成 \(n\times n\times n\) 个小立方体的大立方体,选出其中 \(k\) 个小立方体使得三视图中无立方体相互遮挡,且三视图相同。
Solution
考虑构造一个 \(k=n^2\) 的方案。我们通过俯视图以及每个立方体的高度来表示一种选择立方体的方案。
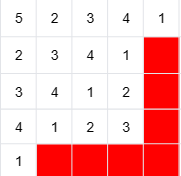
不难想到可以类似 ARC176A 选对角线的方式来使它三视图全部填满。这样填对角线的方式也保证了他的主视图和左视图相同。如下图:
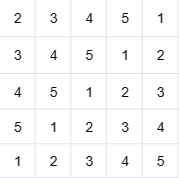
考虑在这个方案中扣掉 \(d = n^2 - k\) 个格子。一种特殊情况比较少的方式是,扣掉右下角反 L 形的一块,如果不够扣就直接扣掉一圈再扣反 L。同时这个反 L 的两段长度最好相同,如果 \(d\) 是偶数的话可以补上右下角一小块。
此时再在扣掉一些格子的俯视图里填数,还是可以一条一条对角线地填。从正中间的对角线开始,为了满足扣掉对角线之后的主视图对高度的限制,往右下方填对角线。令 \(l = \lfloor\frac{d}{2}\rfloor\) 即 反 L 两边长不计右下角。可以发现限制相当于高度在 \([1, n - l)\) 无影响,\([n - l, n - 1]\) 要少填一个,高度正好为 \(n\) 则只要填 \(n - l - 1\) 个。(不记右下角的格子)
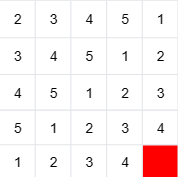
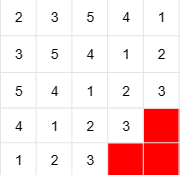
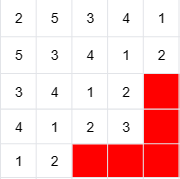
发现对于 \(h\in[n - l, n - 1]\),右下部分的对角线是被扣掉了两个格子,那么为了保证个数,必须搭配左上方比平时多 \(1\) 格子的对角线。而空出来的那一个格子数量为 \(n - l - 1\),刚好可以送给 \(n\) 填。
可能比较难想象,所以这里给出 \(n=5,d=1,3,5,7\) 的方案供读者思考与手玩。
\(\\\)
Code
// LUOGU_RID: 167919374
// STOOOOOOOOOOOOOOOOOOOOOOOOO hzt CCCCCCCCCCCCCCCCCCCCCCCORZ
#include <algorithm>
#include <iostream>
#include <numeric>
#include <vector>
using namespace std;
using LL = long long;
using PII = pair<int, int>;
constexpr int kN = 500 + 1;
int n, k, m;
int a[kN][kN], t[kN];
vector<PII> v[2 * kN];
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> n >> k, m = n * n - k;
for (; m > 2 * n - 1; m -= 2 * n - 1, n--) {
}
t[1] = n - m / 2 - (m % 2);
for (int i = 2; i <= n; i++) {
t[i] = n - (i <= m / 2 + 1);
}
reverse(t + 1, t + n + 1);
for (int i = n - m / 2; i <= n; i++) {
a[n][i] = a[i][n] = -1;
}
if (m % 2 == 0) {
a[n][n] = 0;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
!a[i][j] && (v[i + j].emplace_back(i, j), 0);
}
}
for (int s = n + 1, c = 1; s <= 2 * n; s++, c++) {
for (auto [i, j] : v[s]) {
a[i][j] = c;
}
for (auto [i, j] : v[t[c] - v[s].size() + 1]) {
a[i][j] = c;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (a[i][j] != -1) {
cout << i - 1 << ' ' << j - 1 << ' ' << a[i][j] - 1 << '\n';
}
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号